By applying ASA congruence rule, it is to be established that ΔABC[_≅?]ΔQRP and it is given that BC=RP. What additional information is needed to establish the congruence?
To establish that triangle ABC is congruent to triangle QRP using the ASA (Angle-Side-Angle) congruence rule, we need to follow these steps:
1. Identify the Given Information:
We know that BC=RP. This is one side of the triangles.
2. Identify the Corresponding Vertices:
In triangle ABC, let:
- A correspond to Q
- B correspond to R
- C correspond to P
Therefore, we have:
- Side BC corresponds to side RP.
3. Understand the ASA Congruence Rule:
The ASA congruence rule states that if two angles and the included side of one triangle are equal to two angles and the included side of another triangle, then the two triangles are congruent.
4. Determine What is Needed:
Since we have one side BC=RP, we need two angles that are included between these sides to apply the ASA rule.
5. Identify the Required Angles:
We need to establish that:
- Angle B (in triangle ABC) is equal to Angle P (in triangle QRP).
- Additionally, we also need to know that Angle A (in triangle ABC) is equal to Angle Q (in triangle QRP).
6. Conclusion:
Therefore, the additional information needed to establish the congruence of triangle ABC and triangle QRP using the ASA rule is:
- Angle B = Angle P
- Angle A = Angle Q
Final Statement:
With the additional information that Angle B is equal to Angle P and Angle A is equal to Angle Q, we can conclude that triangle ABC is congruent to triangle QRP by the ASA congruence rule.
---
We know that BC=RP. This is one side of the triangles.
In triangle ABC, let:
- A correspond to Q
- B correspond to R
- C correspond to P
- Side BC corresponds to side RP.
The ASA congruence rule states that if two angles and the included side of one triangle are equal to two angles and the included side of another triangle, then the two triangles are congruent.
Since we have one side BC=RP, we need two angles that are included between these sides to apply the ASA rule.
We need to establish that:
- Angle B (in triangle ABC) is equal to Angle P (in triangle QRP).
- Additionally, we also need to know that Angle A (in triangle ABC) is equal to Angle Q (in triangle QRP).
Therefore, the additional information needed to establish the congruence of triangle ABC and triangle QRP using the ASA rule is:
- Angle B = Angle P
- Angle A = Angle Q
With the additional information that Angle B is equal to Angle P and Angle A is equal to Angle Q, we can conclude that triangle ABC is congruent to triangle QRP by the ASA congruence rule.
Topper's Solved these Questions
Similar Questions
It is given that ΔABC≅ΔRPQ .Is it true to say that BC =QR ? Why ?
View SolutionIn Fig 7.26, can you use ASA congruence rule and conclude that ΔAOC≅ΔBOD ?
View SolutionIt is given that ΔABC≅ΔFDE and AB= 5 cm , ∠B=40∘ and ∠A=80∘ then which of the following is true ?
View SolutionIn the given figure, DE // BC.

Prove that ΔADEandΔABC are similarView SolutionThe angles of a triangle ABC are in A.P. and it is being given that b:c=√3:√2, find ∠A.
View SolutionUse the information marked to prove :
(i) ΔEAC≅ΔDBC (ii) EC=DC
Also state the Euclid's axiom used in proving the congruency of two triangles.
 View Solution
View SolutionD and E are the mid-points of the side AB and AC, respectively, of ΔABC. DE is produced to F. To prove that CF is equal and parallel to DA, we need an additional information which is
View SolutionThe constrution of ΔABC , given that BC = 6cm, ∠B=45∘ is not possible when difference of AB and AC is equal to
View SolutionIn the given figure ΔABC is right angled at A. Semicircles are drawn on AB, BC and AC as diameters. It is given that AB=3 cm and AC=4cm then find the area of the shaded region
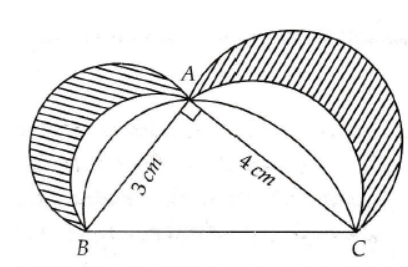 View Solution
View SolutionTheorem 7.4 (SSS congruence rule) : If three sides of one triangle are equal to the three sides of another triangle, then the two triangles are congruent.
View Solution

