In fig 7.13, (i) state the three pairs of equal in (iii) Is ? Why or why not ? (iii) Does bisect ? ? Given reasons
In and , the three pairs of equal parts are as given below:
(Given)
(Given)
and (Common in both)
From above, (By congruence rule)
(Corresponding parts of congruent triangles)
So, bisects .
Topper's Solved these Questions
Similar Questions
In Fig 7.23, AB=ACandAD is the bisector of ? BAC. (i) State three pairs of equal parts in triangles ADBandADC. (ii) Is ΔADB[≡~?]ΔADC ? Given reasons. (iii) Is ∠B=∠C ? Given reasons
View SolutionIn Fig 7.31, DA⊥AB,CB⊥ABandAC=BD. State the three pairs of equal parts in ΔABCandΔDAB. Which of the following statements is meaningful? (i) ΔABC[_≅?]ΔBAD (ii) ΔABC[_≅?]ABD
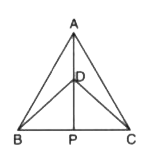
View SolutionThe given figure shows two isosceles triangles ABC and DBC with common base BC. AD is extended to intersect BC at point P. Show that:
ΔABD=ΔACD
(ii) ΔABP=ΔACP
(iii) AP bisects ∠BDC
(iv) AP is perpendicular bisector of BC.
View SolutionIn figure, AB∣∣DC and AB=DC. (i)IsΔACD≅ΔCAB? (ii)State the three pairs of matching parts used to answer (iii) Which angle is equal to∠CAD ? (iv) Does it follow from (iii) that A D || B C ?
View SolutionΔABCand ΔDBCare two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that (i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC

View SolutionIn a triangle ABC, D is mid-point of BC, AD is produced upto E so that DE = AD. Prove that :
(i) ΔABDandΔECD are congruent.
(ii) AB = EC
(iii) AB is parallel to EC.
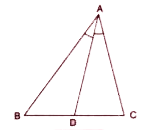
View SolutionIn the figure, given alongside, AD bisects angle BAC. Prove that :
(i) AB>BD
(ii) AC>CD
(iii) AB+AC>BC
View SolutionIn the figure, given alongside, AD bisects angle BAC. Prove that :
(i) AB>BD
(ii) AC>CD
(iii) AB+AC>BC

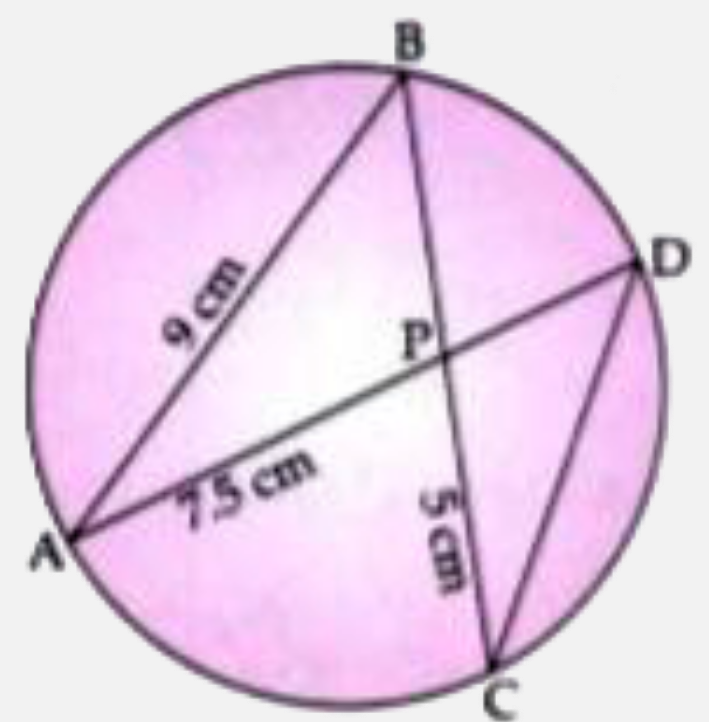
View SolutionIn the figure given figure AB = 9cm, PA = 7.5 cm and PC = 5 cm. Chords AD and BC intersect at P.
(i) Prove that ΔPAB~ΔPCD
(ii) Find the length of CD.
(iii) Find area of ΔPAB : are of ΔPCD
View SolutionIn right triangle ABC, right-angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see Fig. 7.23). Show that:
(i) ΔAMC≅ΔBMD
(ii) ∠DBC is a right angle
(iii) ΔDBC≅ΔACB
(iv) CM=12AB

View Solution
