Question

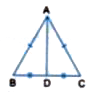
In Fig 7.23, $AB=AC\text{and}AD$ is the bisector of ? $BAC.$ (i) State three pairs of equal parts in triangles $ADB\text{and}ADC.$ (ii) Is $\Delta ADB[\equiv ~?]\Delta ADC$ ? Given reasons. (iii) Is $\angle B=\angle C$ ? Given reasons

Explanation

To solve the given question step by step, we will analyze the information provided and apply the properties of congruent triangles.

Step 1: Identify the Equal Parts in Triangles ADB and ADC
We need to state three pairs of equal parts in triangles ADB and ADC.

1. AB = AC (Given)
2. AD = AD (Common side)
3. ∠BAD = ∠CAD (AD is the bisector of ∠BAC)

Step 2: Check for Congruence of Triangles ADB and ADC
Now, we need to determine if triangle ADB is congruent to triangle ADC.

- We have identified:
- One pair of equal sides: AB = AC
- Another pair of equal sides: AD = AD (common side)
- One pair of equal angles: ∠BAD = ∠CAD

Using the SAS (Side-Angle-Side) congruence criterion, we can conclude:
- Triangle ADB ≅ Triangle ADC (by SAS congruence rule)

Step 3: Determine if Angle B Equals Angle C
Finally, we need to check if ∠B = ∠C.

Since triangles ADB and ADC are congruent, by the property of congruent triangles, we know that corresponding parts of congruent triangles are equal.
- Therefore, ∠B = ∠C.

Summary of the Solution
(i) The three pairs of equal parts in triangles ADB and ADC are:
- AB = AC
- AD = AD
- ∠BAD = ∠CAD

(ii) Yes, triangle ADB is congruent to triangle ADC by the SAS congruence rule.

(iii) Yes, ∠B = ∠C because corresponding parts of congruent triangles are equal.

---