In Fig 7.26, can you use ASA congruence rule and conclude that ΔAOC≅ΔBOD ?
To determine if triangles AOC and BOD are congruent using the ASA (Angle-Side-Angle) congruence rule, we will follow these steps:
Step 1: Identify Given Information
We are given:
- AC = BD (both sides are equal)
- Angle C = Angle D = 70 degrees
- Angle AOC = Angle BOD = 30 degrees (since they are vertically opposite angles)
Step 2: Calculate Angle A and Angle B
Using the angle sum property of triangles, we can find the measures of angles A and B.
For Triangle AOC:
- The sum of angles in a triangle is 180 degrees.
- Therefore, Angle A + Angle C + Angle AOC = 180 degrees.
- Substituting the known values: Angle A + 70 + 30 = 180.
- This simplifies to Angle A + 100 = 180.
- Thus, Angle A = 180 - 100 = 80 degrees.
For Triangle BOD:
- Similarly, we apply the angle sum property.
- Angle B + Angle D + Angle BOD = 180 degrees.
- Substituting the known values: Angle B + 70 + 30 = 180.
- This simplifies to Angle B + 100 = 180.
- Thus, Angle B = 180 - 100 = 80 degrees.
Step 3: Compare Angles and Sides
Now we have:
- Angle A = Angle B = 80 degrees
- Angle C = Angle D = 70 degrees
- AC = BD = 3 (given)
Step 4: Apply the ASA Congruence Rule
According to the ASA rule:
- If two angles and the included side of one triangle are equal to two angles and the included side of another triangle, then the triangles are congruent.
In this case:
- Angle A = Angle B (80 degrees)
- Angle C = Angle D (70 degrees)
- Side AC = Side BD (3 units)
Conclusion
Since we have two pairs of equal angles and the included side is also equal, we can conclude that:
Triangle AOC is congruent to Triangle BOD (ΔAOC ≅ ΔBOD) by the ASA congruence rule.
---
We are given:
- AC = BD (both sides are equal)
- Angle C = Angle D = 70 degrees
- Angle AOC = Angle BOD = 30 degrees (since they are vertically opposite angles)
Using the angle sum property of triangles, we can find the measures of angles A and B.
- The sum of angles in a triangle is 180 degrees.
- Therefore, Angle A + Angle C + Angle AOC = 180 degrees.
- Substituting the known values: Angle A + 70 + 30 = 180.
- This simplifies to Angle A + 100 = 180.
- Thus, Angle A = 180 - 100 = 80 degrees.
- Similarly, we apply the angle sum property.
- Angle B + Angle D + Angle BOD = 180 degrees.
- Substituting the known values: Angle B + 70 + 30 = 180.
- This simplifies to Angle B + 100 = 180.
- Thus, Angle B = 180 - 100 = 80 degrees.
Now we have:
- Angle A = Angle B = 80 degrees
- Angle C = Angle D = 70 degrees
- AC = BD = 3 (given)
According to the ASA rule:
- If two angles and the included side of one triangle are equal to two angles and the included side of another triangle, then the triangles are congruent.
- Angle A = Angle B (80 degrees)
- Angle C = Angle D (70 degrees)
- Side AC = Side BD (3 units)
Since we have two pairs of equal angles and the included side is also equal, we can conclude that:
Triangle AOC is congruent to Triangle BOD (ΔAOC ≅ ΔBOD) by the ASA congruence rule.
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLESBook:NCERT ENGLISHChapter:CONGRUENCE OF TRIANGLESExercise:EXERCISE 7.1
Explore 4 Videos
- COMPARING QUANTITIESBook:NCERT ENGLISHChapter:COMPARING QUANTITIESExercise:EXERCISE 8.2
Explore 10 Videos
- DATA HANDLINGBook:NCERT ENGLISHChapter:DATA HANDLINGExercise:EXERCISE 3.2
Explore 5 Videos
Similar Questions
By applying ASA congruence rule, it is to be established that ΔABC[_≅?]ΔQRP and it is given that BC=RP. What additional information is needed to establish the congruence?
View SolutionBE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
View SolutionGiven below are measurements of some parts of two triangles. Examine whether the two triangles are congruent or not, by using SAS congruence rule. If the triangles are congruent, write them in symbolic form. ΔDEF
View SolutionIn Fig 7.31, DA⊥AB,CB⊥ABandAC=BD. State the three pairs of equal parts in ΔABCandΔDAB. Which of the following statements is meaningful? (i) ΔABC[_≅?]ΔBAD (ii) ΔABC[_≅?]ABD
View Solution
¯¯¯¯¯¯ACand¯¯¯¯¯¯BD are diameters of circle E above. Which triangle congruence theorem can be used to prove that △AEB is congruent to △DEC?
View SolutionABC is an isosceles triangle with AB=AC and D is a point on ABC BC such that AD⊥BC (see figure ). To prove that ∠BAD=∠CAD a student proceeded as follows
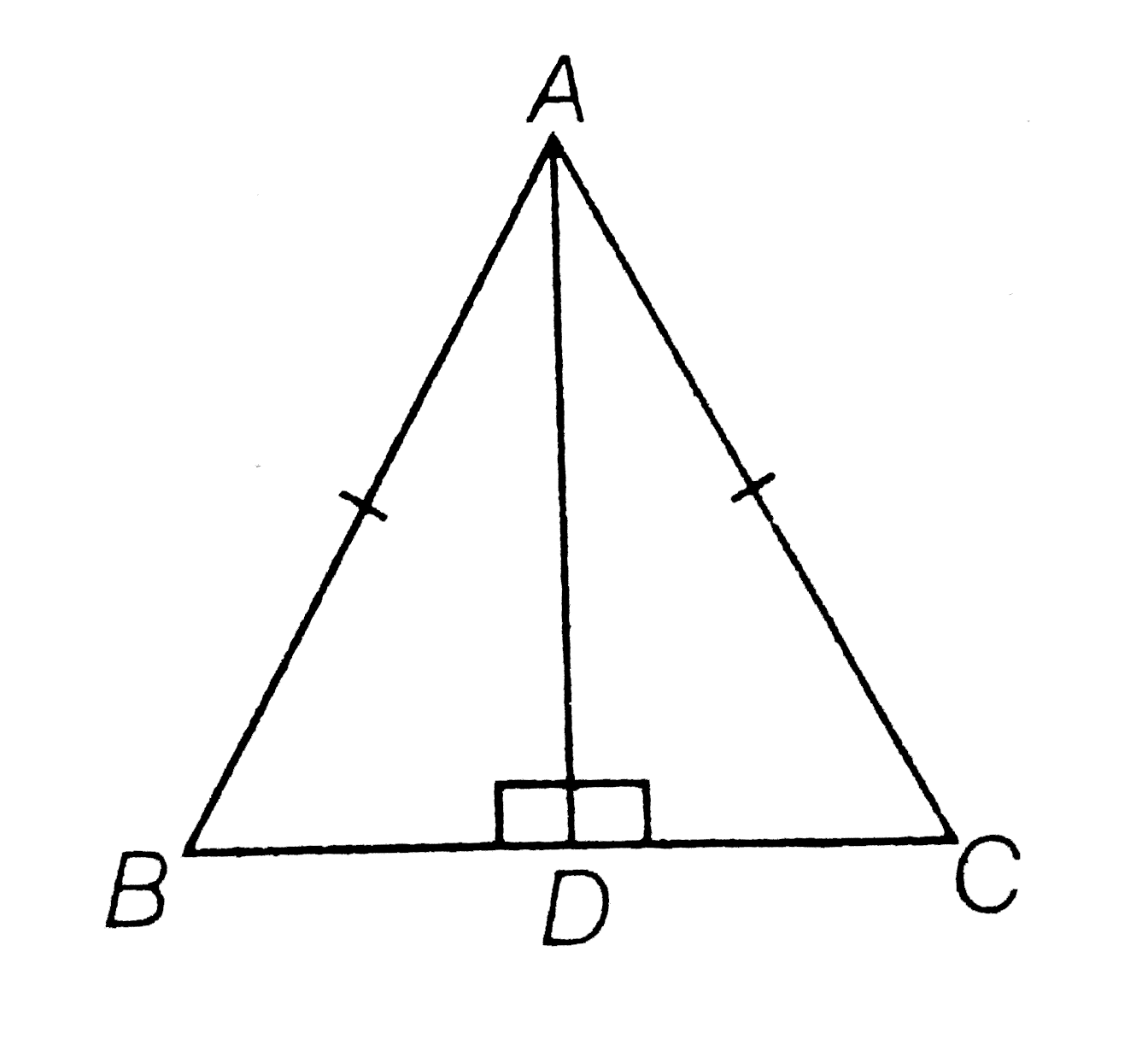
InΔABDandΔACD,we have
AB=AC [ Given]
∠B=∠C [∵ AB=AC ]
and ∠ADB=∠ADC
Therefore ΔABD≅ΔACD [by AAS congruence rule]
So , ∠BAD=∠CAD [byCPCT]
What is the defect in the above argument ?
View SolutionEffect of temperature on the equilibrium process analysed by using the thermodynamics
From the thermodynamics reaction
ΔG∘=−2.30RTlogk
ΔG∘: Standing free energy change
ΔG∘=ΔH∘−TΔS∘…(ii)
ΔH∘:Standard heat of the reaction gt
From eqns.(i) and(ii)
−2RTlogk=ΔH∘=TΔS∘
ΔS∘ : standard entropy change
⇒ logK=−ΔH∘2.3RT+ΔS∘2.3R
Clearly, if a plot of k vs 1/T is made then it is a straight lone having slope =−ΔH∘2.3R amd y intercept =ΔS∘2.3R
If at temperature T1 equilibrium constant be k1 and at temperature T2equilibrium constant be k2 then :
⇒ logK1=−ΔH∘2.3RT1+ΔS∘2.3R..(iv)
⇒ logK2=−ΔH∘2.3RT2+ΔS∘2.3R...(v)
Substracting e.q (iv) from (v), we get
from the relation we can conclude that the of equilibrium constant increase in temperature for endothermic reaction eith but value of equilibrium constant decrease with the increase in temperature for exothermic reaction
For exothermic reaction if ΔS∘<0 then the sketch of log k vs 1T may be
View SolutionEffect of temperature on the equilibrium process analysed by using the thermodynamics
From the thermodynamics reaction
ΔG∘=−2.30RTlogk
ΔG∘: Standing free energy change
ΔG∘=ΔH∘−TΔS∘…(ii)
ΔH∘:Standard heat of the reaction gt
From eqns.(i) and(ii)
−2RTlogk=ΔH∘=TΔS∘
ΔS∘ : standard entropy change
⇒ logK=−ΔH∘2.3RT+ΔS∘2.3R
Clearly, if a plot of k vs 1/T is made then it is a straight lone having slope =−ΔH∘2.3R amd y intercept =ΔS∘2.3R
If at temperature T1 equilibrium constant be k1 and at temperature T2equilibrium constant be k2 then :
⇒ logK1=−ΔH∘2.3RT1+ΔS∘2.3R..(iv)
⇒ logK2=−ΔH∘2.3RT2+ΔS∘2.3R...(v)
Substracting e.q (iv) from (v), we get
from the relation we can conclude that the of equilibrium constant increase in temperature for endothermic reaction eith but value of equilibrium constant decrease with the increase in temperature for exothermic reaction
If for a particular reversible reaction
KC=57 abd 355∘C and KC=69 at 450∘C then
View SolutionEffect of temperature on the equilibrium process analysed by using the thermodynamics
From the thermodynamics reaction
ΔG∘=−2.30RTlogk
ΔG∘: Standing free energy change
ΔG∘=ΔH∘−TΔS∘…(ii)
ΔH∘:Standard heat of the reaction gt
From eqns.(i) and(ii)
−2RTlogk=ΔH∘=TΔS∘
ΔS∘ : standard entropy change
⇒ logK=−ΔH∘2.3RT+ΔS∘2.3R
Clearly, if a plot of k vs 1/T is made then it is a straight lone having slope =−ΔH∘2.3R amd y intercept =ΔS∘2.3R
If at temperature T1 equilibrium constant be k1 and at temperature T2equilibrium constant be k2 then :
⇒ logK1=−ΔH∘2.3RT1+ΔS∘2.3R..(iv)
⇒ logK2=−ΔH∘2.3RT2+ΔS∘2.3R...(v)
Substracting e.q (iv) from (v), we get
from the relation we can conclude that the of equilibrium constant increase in temperature for endothermic reaction eith but value of equilibrium constant decrease with the increase in temperature for exothermic reaction
If statndard heat of dissociation of PCl5 is 230 cal then slope of the graph of log vs 1T is :
View SolutionTheorem 7.4 (SSS congruence rule) : If three sides of one triangle are equal to the three sides of another triangle, then the two triangles are congruent.
View Solution
