Locate the centre of mass of uniform triangular lamina and a uniform cone.
The lamina (ΔLMN) may be subdivided into narrow strips each parallel to the base (MN) as shown in Fig. 7.10
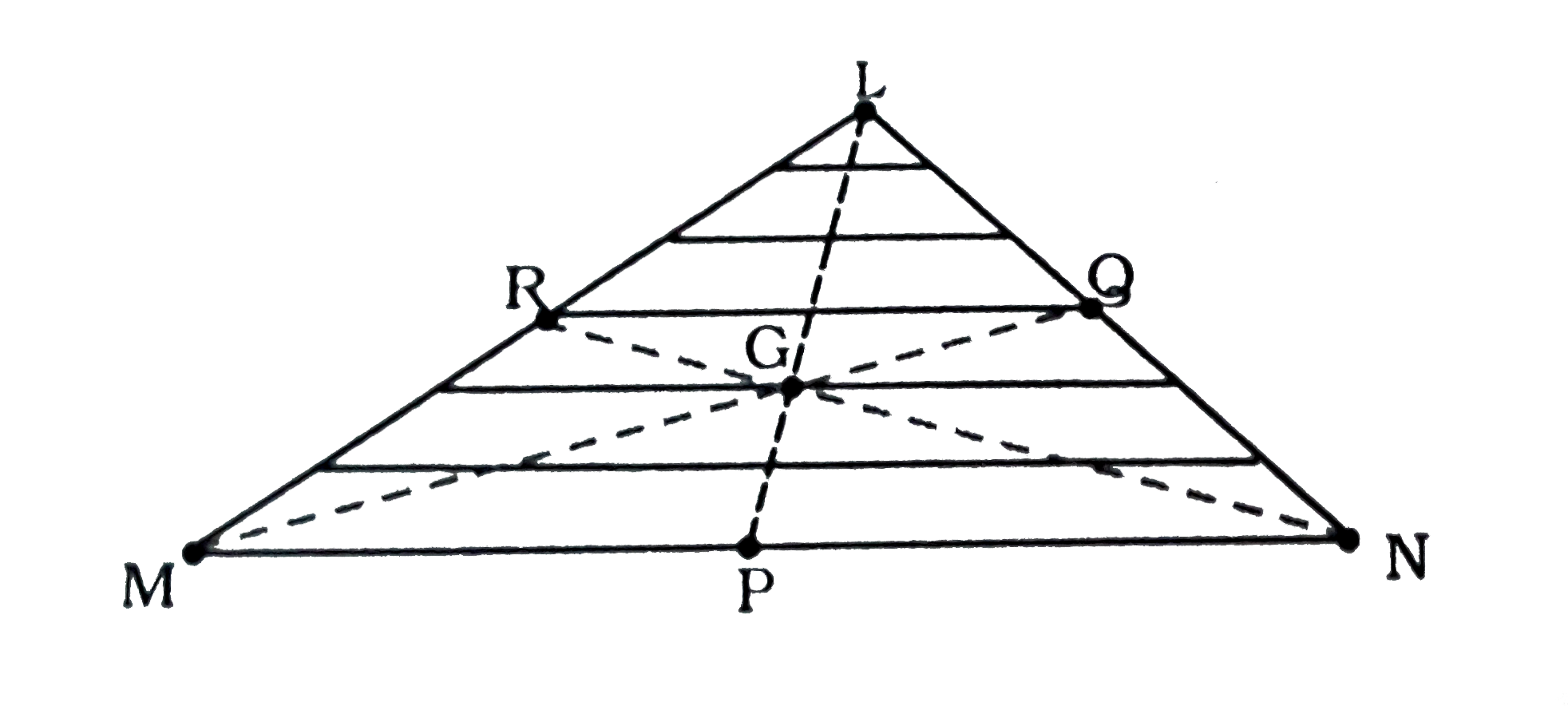
By symmetry each strip has its centre of mass at its midpoint. If we join the midpoint of all the strips we get the median LP. The centre of mass of the triangle as a whole therefore, has to lie on the median LP. Similarly, we can argue that it lies on the median MQ and NR. This means the centre of mass lies on the point of concurrence of the medians, i.e. on the centroid G of the triangle.
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - NCERT ENGLISHCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISE
33 Videos
- PHYSICAL WORLD BOOK - NCERT ENGLISHCHAPTER - PHYSICAL WORLD EXERCISE - EXERCISE
16 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXERCISE
22 Videos
Similar Questions
Find the centre of mass of a uniform triangula lamina.
View SolutionFind the centre of mass of a uniform triangula lamina.
View SolutionWhat is the location of the centre of mass of a uniform triangular lamina ?
View SolutionFind the centre of mass of a uniform triangula lamina.
View SolutionProve that the centre of mass of a uniform triangular plate coincides with the point of intersection of its medians.
View SolutionCentre Of Mass Of Uniform Rod
View SolutionFind the centre of mass of a uniform solid cone.
View SolutionFind the centre of mass of a uniform solid cone.
View SolutionTwo identical uniform rods AB and CD, each of length L are jointed to form a T-shaped frame as shown in figure. Locate the centre of mass of the frame. The centre of mass of a uniform rod is at the middle point of the rod.

View SolutionThe coordinates of the centre of mass of a uniform flag -shaped lamina (thin flat plate) of mass 4kg .( The coordinates of the same are shown in the figure) are :
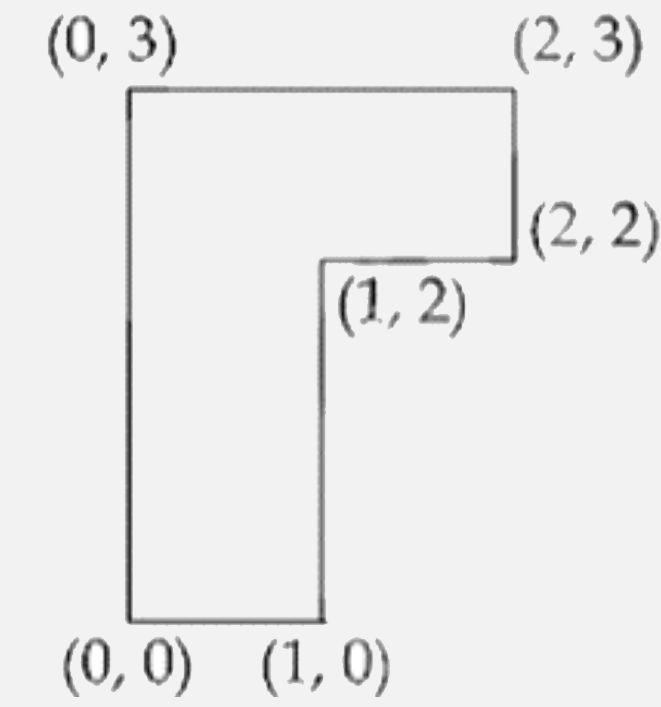
View Solution
