एक गोलीय सममित आवेश वितरण जिसमें आवेश घनत्व इस प्रकार परिवर्तित होता है ρ(r)=0,ρ0(54−rR),r=R तक और ρ(r),r>R के लिये , जहाँ, मूलबिन्दु से दूरी है | मूलबिन्दु से दूरी r(r<R) पर विद्युत क्षेत्र इस प्रकार दिया जाता है
ρ0r4ε0(54−rR)
4πρ0r3ε0(53−rR)
ρ0r4ε0(53−rR)
4ρ0r3ε0(54−rR)
The correct Answer is:C
कुल आवेश Q=∫r0ρd=∫r0ρ0(54−rR)4πr2dr
4πρ0∫r0(5r24−r3R)dr=4πρ0[5r312−r44R]
E=KQr2=14πε0r24πρ0[512r3−r44R]=ρ0r4ε0[53−rR]
Topper's Solved these Questions
- स्थिर वैद्युतBOOK - ERRORLESS HINDICHAPTER - स्थिर वैद्युतEXERCISE - Graphical Questions
13 Videos
- स्थिर वैद्युतBOOK - ERRORLESS HINDICHAPTER - स्थिर वैद्युतEXERCISE - JEE Section (More than one correct answers)
17 Videos
- स्थिर वैद्युतBOOK - ERRORLESS HINDICHAPTER - स्थिर वैद्युतEXERCISE - Ordinary Thinking (संधरित्रों का संयोजन)
91 Videos
- सरल आवर्त गति BOOK - ERRORLESS HINDICHAPTER - सरल आवर्त गति EXERCISE - Self Evaluation Test (सरल आवर्त गति )
19 Videos
Similar Questions
दिए गये परिपथ में, C के मान के 1μF से 3μF परिवर्तित होने से, 2μF संधारित्र पर आवेश Q2 में परिवर्तन होता है। के पहलन के रूप में Q2 को कौन-सा आलेख सही दर्शाता है? (आलेख केवल व्यवस्था आरेख है और स्केल के अनुसार नहीं है।)
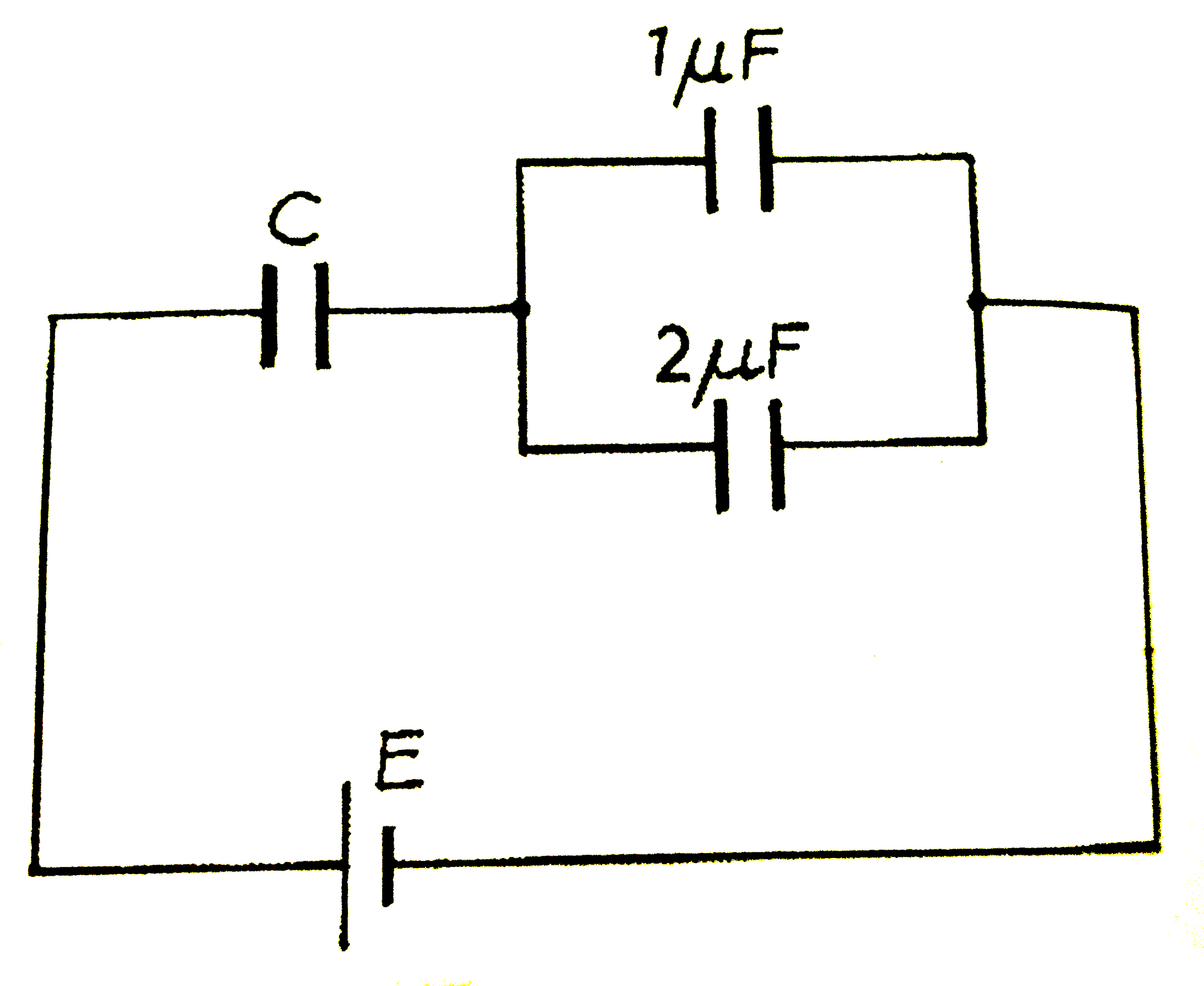
View Solutionविद्युत क्षेत्र की तीव्रता का मात्रक एवं विमा लिखिए
View Solutionसंधारित्रों से बने एक परिपथ को चित्र में दिखाया गया है| एक बिन्दु - आवेश Q ( जिसका मान 4μF तथा 9μF वाले संधारित्रों के कुल आवेशों के बराबर है ), के द्वारा 30m दूरी पर वैद्युत-क्षेत्र का परिमाण होगा
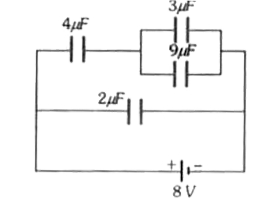
View Solutionएक सरल लोलक , का गोलक एक धात्विक खोकला गोला है। इसका आवर्तकाल T है। जब गोलक में रेत भरी है। तब आवर्तकाल T1 है जब यह मरकरी से भरा है तब आवर्तकाल T2 है जब यह मरकरी से आधा भरा है तब इसका आवर्तकाल T3 है । तब निम्न में से सही विकल्प है।
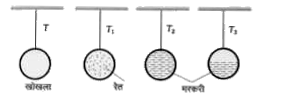
View SolutionA non-homogenous sphere of radius R has the following density variation.
ρ=ρ0,r≤r/3,
ρ=ρ0/2,R3<r≤3R4,
ρ=ρ08,(3R)/(4)<r≤R,
What is the gravitational field due to sphere at distance 2R from center?
View SolutionA non-homogeneous sphere of radius R has the following density variation : rho{{:(rho_(0),rleR//3),(rho_(0)//2,(R//3) lt r le (3R//4)),(rho_(0)//8,(3R//4) lt r le R):} The gravitational field at a distance 2R from the centre of the sphere is
View SolutionA solid ball of radius R has a charge density rho given by rho = rho_(0)(1-(r )/(R )) for 0le r le R The electric field outside the ball is :
View SolutionConsider a solid sphere oFIGURE radius R and mass density rho(r)=rho_(0)(1-(r^(2))/(R^(2))) 0 lt r le R . The minimum density oFIGURE a liquid in which it will FIGUREloat is:
View SolutionNaCl प्रकार की संरचना वाले क्रिस्टल में r++r−_=……… होते है। जहाँ a इकाई सैल के किनारे की लम्बाई है।
View Solution[" Consider a spherical symmetric "],[" charge distribution with charge "],[" density varying as "],[[rho={[rho_(0)(1-(r)/(R)),r R]]
View Solutionयदि संक्रिया ∗ वास्तविक संख्याओं के समुच्चय R पर द्विआधारी संक्रिया है तथा इस प्रकार परिभाषित है कि
a∗b=√a4+b4 , जहाँ a,b∈R से दिखाइए कि '∗' क्रम-विनिमेय नियम का पालन करती है।
View Solutionयदि f:R→R इस प्रकार है कि f(x) = |x|, तो सिद्ध कीजिए कि fof = f .
View SolutionA solid sphere of density ρ=ρ0(1−r2R2),0<r≤R just floats in a liquid, then the density of the liquid is (r is the distance from the centre of the sphere)
View SolutionA solid ball of radius R has a charge density rho given by rho = rho_(0)(1-(r )/(R )) for 0le r le R The electric field outside the ball is :
View SolutionConsider a solid sphere oF radius R and mass density ρ(r)=ρ0(1−r2R2) 0<r≤R. The minimum density oF a liquid in which it will Float is:
View SolutionA non-homogeneous sphere of radius R has the following density variation : rho{{:(rho_(0),rleR//3),(rho_(0)//2,(R//3) lt r le (3R//4)),(rho_(0)//8,(3R//4) lt r le R):} The gravitational field at a distance 2R from the centre of the sphere is
View Solution
