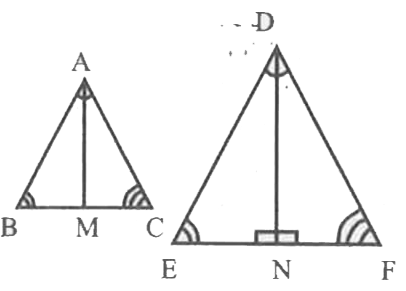
Prove that “the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides”.Solution in Kannada
Step by step video & image solution for Prove that “the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides”. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SOLVED PAPER (SSLC KARNATAKA APRIL 2019)BOOK - OSWAAL PUBLICATIONCHAPTER - SOLVED PAPER (SSLC KARNATAKA APRIL 2019)EXERCISE - Answer the following :
29 Videos
- REAL NUMBERSBOOK - OSWAAL PUBLICATIONCHAPTER - REAL NUMBERSEXERCISE - TEXTBOOK CORNER ( EXERCISE 8.4 )
12 Videos
- SOLVED PAPER SSLC KARNATAKA JUNE 2020 BOOK - OSWAAL PUBLICATIONCHAPTER - SOLVED PAPER SSLC KARNATAKA JUNE 2020 EXERCISE - Answer the following questions
37 Videos
Similar Questions
The given graph represents a pair of linear equations in two variables. Write how many solutions these pair of equations have.

View SolutionWithout actually performing the long division state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion
133125
View SolutionExpress the denominator of 23/20 the form of 2n×5m and state whether the given fraction is terminating or non-terminating repeating decimal.
View SolutionProve that the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.
View SolutionThe ratio of area of Two similar triangles is equal to the ratio of the squares of any two corresponding sides.
View SolutionThe ratio of the the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides/altitudes.
View SolutionTheorem 6.6 : The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
View SolutionThe ratio of areas of two similar triangles is equal to the ratio of the squares of corresponding…….
View SolutionProve that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
View SolutionProve that " the ratio of areas of two similar triangles is equal to the square of the ratio of their altitudes.
View Solutionprove that The areas of the two similar triangles are in the ratio of the square of the corresponding medians.
View SolutionProve that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
View SolutionProve that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
View SolutionTheorem 6.6 : The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
View SolutionProve that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
View SolutionProve that the ratio of the areas of two similar triangles is equal to the ratio of the squares of the corresponding altitudes of the triangles.
View Solution
