Two point charges +q and -2qare placed at the vertices B and C of an equilateral triangle ABC of side 'a' as shown in Obtain the expression for
The magnitude ,
(b)
The direction of the resultant electric field at the vertex A due to these two charges.
(c)
As shown in electric field at vertex A due to charge +q placed at vertex B is
EB=14π∈0.qa2 along BA
and electrical field at vertex A due to charges -2q placed at vertex C is
EC=14π∈02qa2 along AC
Obviously −→EBand−→EC are inclined at an angle θ=120∘ from the another . Hence
Magnitude of net electric field at A
E=√E2B+E2C+2EBECcos120∘=√E2B+E2C−EBEC
⇒ E=14π∈0.√3qa2
(b) If the net electric field →E is directed at angle β from the direction AC, then
tanβ=EBsin120∘EC+EBcos120∘=EB.(√3/2)EC−(EB/2)=EB.(√3/2)2EB−(EB/2)
⇒ tanβ=1√3orβ=tan−1(1√3)=30∘
 <span class=) <br><imgsrc=hps:/d10lpgp6xz60nq.cloudont.≠tphysicsima≥sULIKSPPHYXIIC01E10020_S02##)
<br><imgsrc=hps:/d10lpgp6xz60nq.cloudont.≠tphysicsima≥sULIKSPPHYXIIC01E10020_S02##)
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS Book:U-LIKE SERIESChapter:ELECTRIC CHARGES AND FIELDS Exercise:LONG ANSWER QUESTIONS -II
Explore 9 Videos
- ELECTRIC CHARGES AND FIELDS Book:U-LIKE SERIESChapter:ELECTRIC CHARGES AND FIELDS Exercise:SELF ASSESSMENT TEST (SECTION-A)
Explore 5 Videos
- ELECTRIC CHARGES AND FIELDS Book:U-LIKE SERIESChapter:ELECTRIC CHARGES AND FIELDS Exercise:SHORT ANSWER QUESTIONS
Explore 29 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:U-LIKE SERIESChapter:DUAL NATURE OF RADIATION AND MATTERExercise:SELF ASSESSMENT TEST SECTION-C (VERY SHORT ANSWER QUESTIONS)
Explore 3 Videos
- ELECTROMAGNETIC WAVESBook:U-LIKE SERIESChapter:ELECTROMAGNETIC WAVESExercise:SELF ASSESSMENT TEST (SECTION C)
Explore 1 Video
Similar Questions
Two point charges +q and -2q are placed at the vertices B and C of an equilateral triangle ABC of side 'a' as shown Obtain the expession for (i) the magnitude ,and (ii) the direction of the resultant electric field at the vertex A due to these two charges .
View SolutionTwo point charges +6qand−8q are placed at the vertices B and C of an equilateral triangle ABC of side a. Obtain an expression for magnitude and direction of resultant electric field at the vertex A due to these two charges.
View Solution
Knowledge Check
Equal charges q are placed at the vertices A and B of an equilatral triangle ABC of side a. The magnitude of electric field at the point C is
Aq4πε0a2B√2q4πε0a2C√3q4πε0a2Dq2πε0a2As shown in the figure, charges +qand−q are placed at the vertices B and C of an isoscles triangle. The potential at the vertex A is
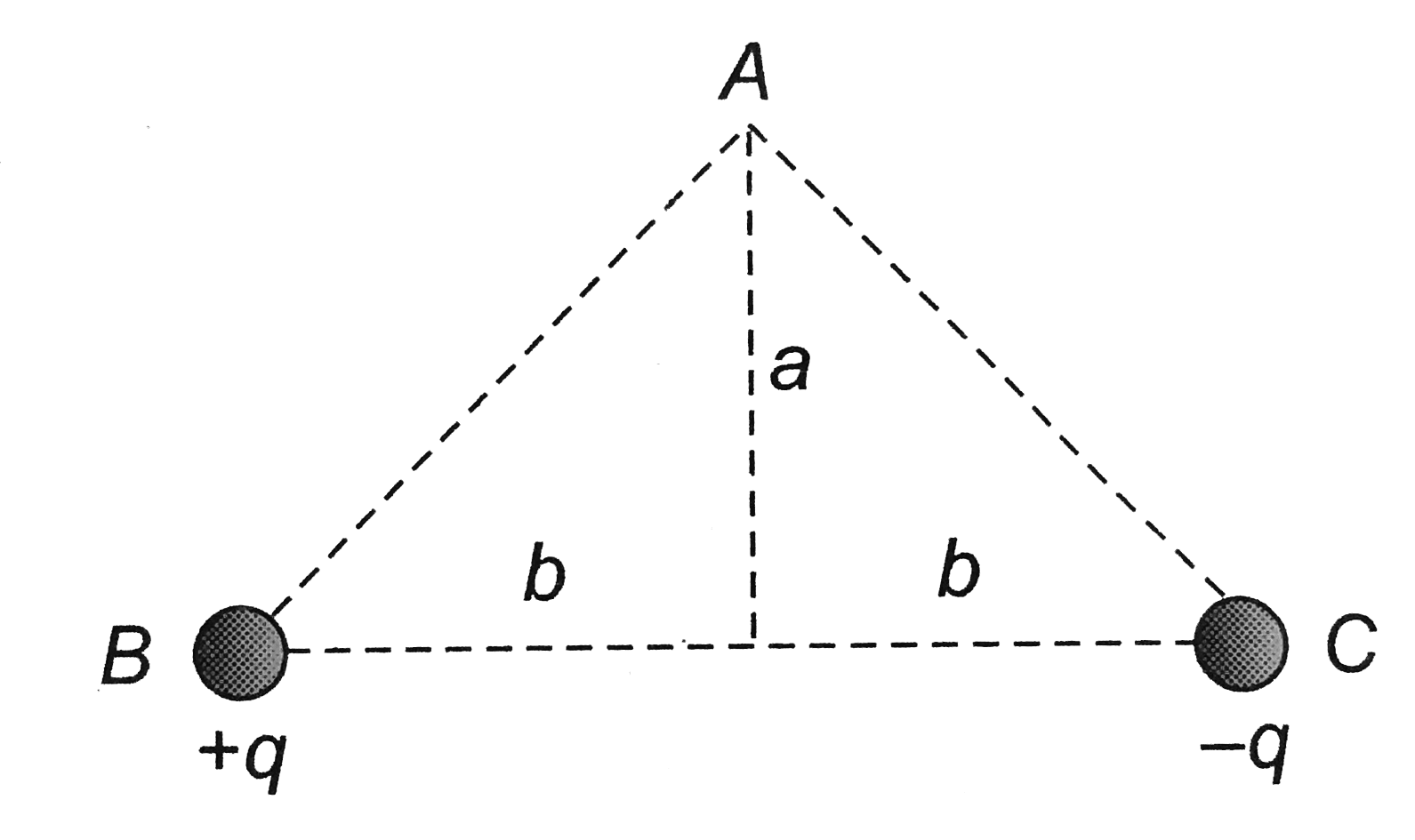 A14πε0.2q√a2+b2BZeroC14πε0.q√a2+b2D14πε0.(−q)√a2+b2
A14πε0.2q√a2+b2BZeroC14πε0.q√a2+b2D14πε0.(−q)√a2+b2
(a) Three point charges q,-4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q.
(b) Find out the amount of the work done to separate the charges at infinite distance.

View SolutionThree point charges q,−4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the Fig. Obtain the experssion for the magnitude of the resultant electric force acting on the charge q.
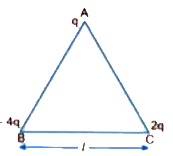
View Solution(a) Three point charges q,-4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q.
(b) Find out the amount of the work 4one to separate the charges at infinite distance.

View Solution(a) Three point charges q,-4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q.
(b) Find out the amount of the work 4one to separate the charges at infinite distance.

View SolutionEqual charges q are placed at the vertices A and B of an equilatral triangle ABC of side a. The magnitude of electric field at the point C is
View SolutionAs shown in the figure, charges +qand−q are placed at the vertices B and C of an isoscles triangle. The potential at the vertex A is

View Solution
