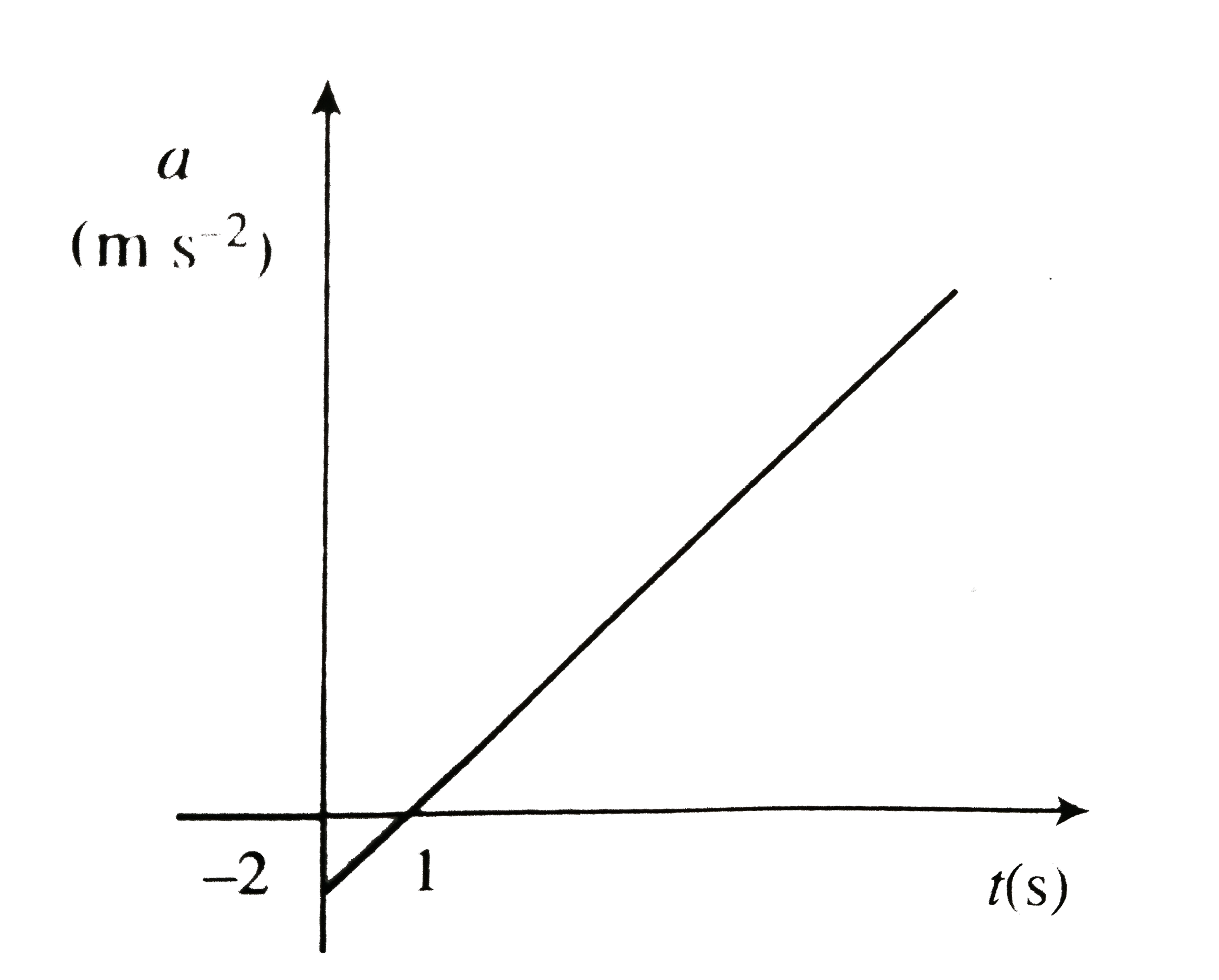
The accelerating of particle varies with time as shown

(a)Find an expression for velocity in terms of t.
(b)Calculate the displacement of the particle in the interval from t=2stot4s.Assume that v=0at t=0Solution in Telugu
(a)t2-2t, (b) 203m
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Short answer type question
12 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question
15 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Numerical exercise(LEVEL-2)
26 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III
45 Videos
Similar Questions
If the average velocity of an object is zero some time interval,What can you say about the displacement of the object for that interval?
View SolutionGive two examples of the motion of big objects where the object can be treated as a particle and where it cannot be?
View SolutionA cyclist takes two minutes to compete half revolution on a circular path of 120 m radius.What is his average speed?
View SolutionA particle is projected over a triangle from one end of a horizontal base and garzing the vertex falls on the other end of the base . If α and β the base angles and θ the angle of projection then show that tanθ=tanα+tanβ.
View SolutionA proton, a deuteron and an a particle having same momentum enter a uniform magnetic field at right angles to the field. Then the ratio of their angular momenta during their motion in the magnetic field is
View SolutionVelocity of a particle moving in a straight line varies with its displacement as v=(√4+4s)m/s. Displacement of particle at time t=0 is s=0. Find displacement of particle at time t=2s.
View SolutionThe acceleration of particle varies with time as shown.

(a) Find an expression for velocity in terms of t.
(b) Calculate the displacement of the particle in the interval from t=2s to t=4s. Assume that v=0 at t=0.
View SolutionDisplacement of a particle of mass 2 kg varies with time as s=(2t^(2)-2t + 10)m . Find total work done on the particle in a time interval from t=0 to t=2s .
View SolutionThe acceleration of a particle varies with time as shown in .
 .
.
a. Find an expression for velocityinterms of t. Assume that v=0 at t=0
b. Calculate the displacement of the paarticle in the time interval from t=2s s.
View SolutionSuppose that a particle mvoes on a straight line so that is velocity at time t is v(t)=(t^(2)-2t)m//s . (a). Find the displacement of the particle during the time interval 0 le t le 3 (b). Find the distance traveled by the particle during the time interval 0 le t le 3 .
View SolutionVelocity of particle of mass 2kg varies with time t accoridng to the equation →v=(2tˆi+4ˆj)ms−1. Here t is in seconds. Find the impulse imparted to the particle in the time interval from t=0 to t=2s.
View SolutionVelocity of a particle varies with time as v=4t. Calculate the displacement of particle between t=2 to t=4 sec.
View SolutionThe displacement x of a particle varies with time 't' as, x=3t2−4t+30. Find the position, velocity and acceleration of the particle at t = 0.
View SolutionPower supplied to a particle of mass 4 kg varies with time as P=(3t^(2))/(2) watt. Here t in second. If velocity of particle at t = 0 is v = 0, the velocity of particle at time t = 2s will be
View SolutionThe acceleration of a particle varies with time t as a=t^(2)+t+2 where t is in seconds. The particle starts with an initial velocity v-3m/s at t=0. find the velocity of the particle at the end of 5s.
View SolutionThe acceleration of a particle varie with time as shown in the figure Find the displacement of the particle in the interval from 1 = 2s to t = 4s Assume that v = 0 at t=0
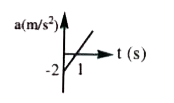
View Solution
