Velocity of particle of mass 2kg varies with time t accoridng to the equation →v=(2tˆi+4ˆj)ms−1. Here t is in seconds. Find the impulse imparted to the particle in the time interval from t=0 to t=2s. Solution in Gujrati
Impulse=Change in momentum=m(→v2−→v1)
=2×[(4ˆi+4ˆj)−(4ˆj)]=8ˆikgms−1
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-I
52 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-II
112 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLEN CHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
Similar Questions
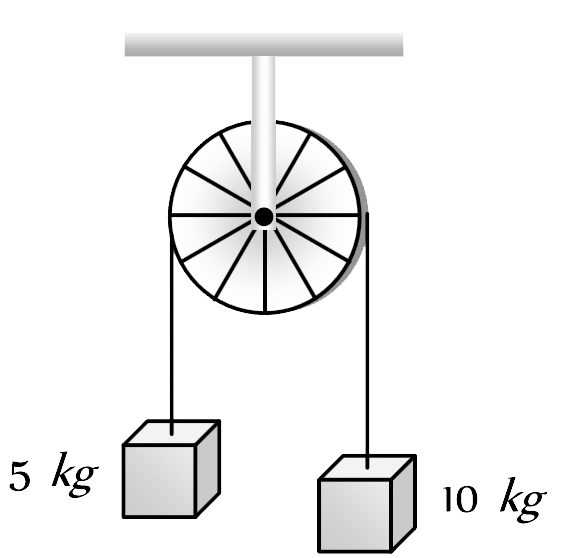
USS 150) Two masses of 5 kg and 10 kg are connected to a pulley as shown. What will be the acceleration of the system (g= acceleration due to gravity)
View SolutionA particle is in straight line motion with uniform velocity A force is not required
View SolutionAssertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.
View SolutionA piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
View SolutionDisplacement of a particle of mass 2 kg varies with time as s=(2t^(2)-2t + 10)m . Find total work done on the particle in a time interval from t=0 to t=2s .
View SolutionThe displacement of a particle of mass 2kg moving in a straight line varies with times as x = (2t^(3)+2)m . Impulse of the force acting on the particle over a time interval between t = 0 and t = 1 s is
View Solution2 किग्रा द्रव्यमान के एक कण का वेग →v समय t के साथ समीकरण →v=(2tˆi+4ˆj) मीटर/सेकण्ड के अनुसार बदल रहा है । कण पर t=0 से t=2 सेकण्ड अन्तराल में कार्यरत आवेग की गणना कीजिए।
View SolutionPower supplied to a particle of mass 4 kg varies with time as P=(3t^(2))/(2) watt. Here t in second. If velocity of particle at t = 0 is v = 0, the velocity of particle at time t = 2s will be
View SolutionThe acceleration of a particle in ms^(-2) is given by a=3t^(2)+2t+2 , where time t is in second. If the particle starts with a velocity v=2 ms^(-1) at t = 0, then find the velocity at the end of 2s.
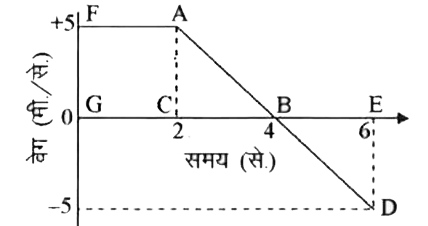
View Solutionसंलग्न चित्र में एकविमीय गति करने वाले कण के लिये वेग - समय आरेख दर्शाया गया है | इस कण के लिए
(i ) समय t = 1 सेकण्ड पर त्वरण
(ii ) समय t = 3 सेकण्ड पर त्वरण तथा
(iii ) समय अंतराल t = 0 सेकण्ड से t = 6 सेकण्ड में कण द्वारा तय की गयी दुरी व कण का विस्थापन ज्ञात करो |
View SolutionThe acceleration of a particle varies with time t as a=t^(2)+t+2 where t is in seconds. The particle starts with an initial velocity v-3m/s at t=0. find the velocity of the particle at the end of 5s.
View SolutionIf velocity (in ms^(-1) ) varies with time as V = 5t, find the distance travelled by the particle in time interval of t = 2s to t = 4 s.
View SolutionVelocity-time equation of a particle moving in a straight line is v=2t-4 for t le 2s and v= 4-2t for 1 gt 2s . The distance travelled ( in meters) by the particle in the time interval from t=0 to t=4s is 4k. The value of 'k' is ( Here t is in second and v in m/s) :
View SolutionThe acceleration of a particle varie with time as shown in the figure Find the displacement of the particle in the interval from 1 = 2s to t = 4s Assume that v = 0 at t=0
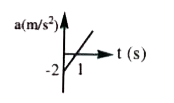
View SolutionThe accelerating of particle varies with time as shown

(a)Find an expression for velocity in terms of t.
(b)Calculate the displacement of the particle in the interval from t=2stot4s.Assume that v=0at t=0
View Solution
