In the adjoining figure, AB is a diameter of the circle with centre O. If AC and BD are perpendiculars on a line PD, and BD meets the circle at E, prove that AC = ED
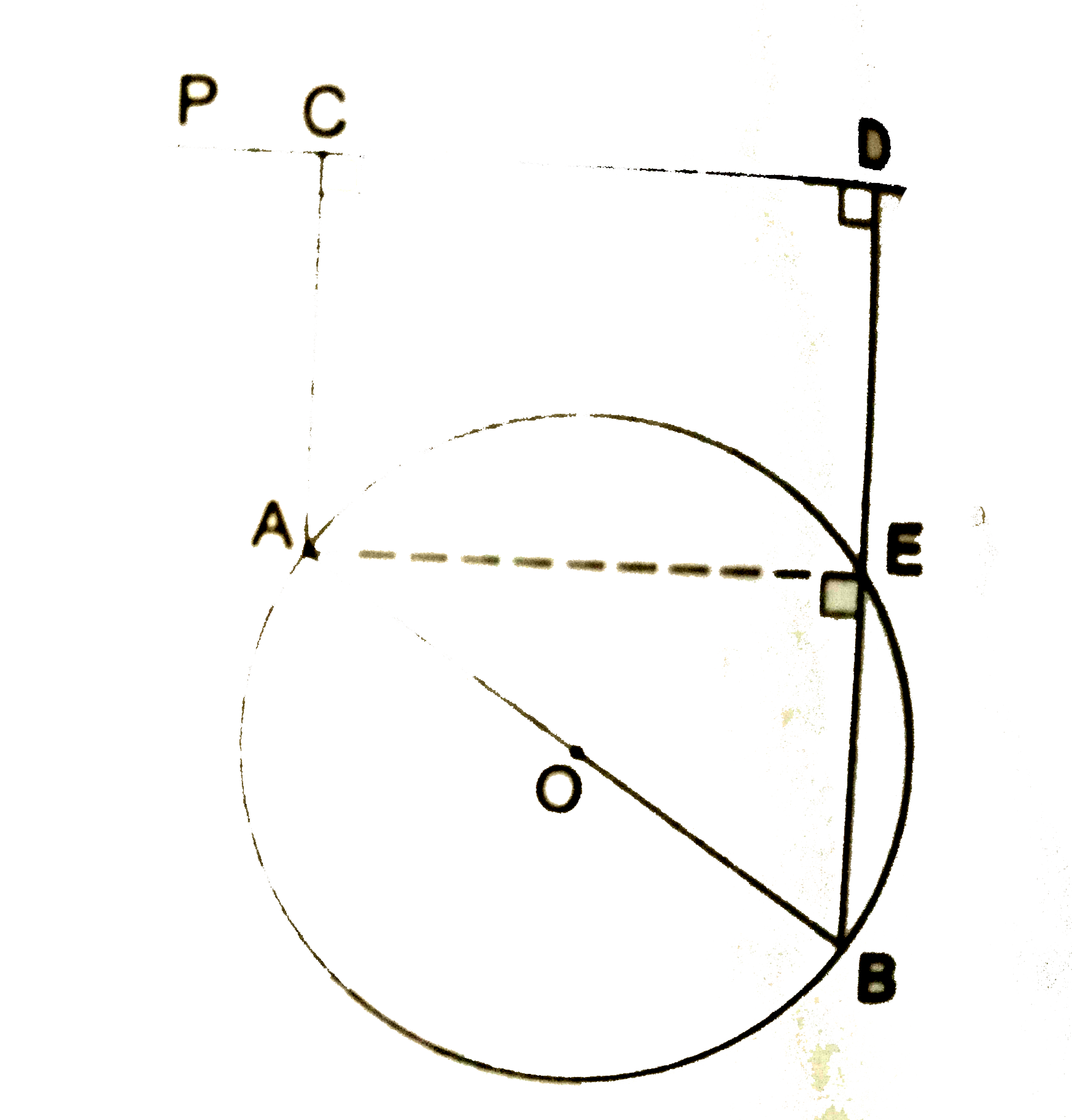
Join AE.
Now, ∠AEB=90∘ [ angle in a semicircle. ]
But, BED being a straight line, we have
∠AEB+∠AED=180∘
⇒90∘+∠AED=180∘
⇒∠AED=90∘
Now, ∠EAC+∠ACD+∠CDE+∠AED=360∘ [sum of the ∠s of quad. EACD is 360∘ ]
⇒∠EAC+90∘+90∘+90∘=360∘
⇒∠EAC=90∘
Thus, each angle of quad. EACD is 90∘.
So, EACD is a rectangle.
:AC=ED [opposite sides of a rectangle].
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Exercise 12A22videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12B18videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B16videos
BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGON
- BOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)20videos
CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLE
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure, AC is the diameter of the circle with centre O. Chord BD is perpendicular to AC. Express p in terms of x.
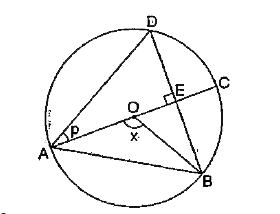 Ax/2B90∘+x/2C90∘−x/2D180∘−x
Ax/2B90∘+x/2C90∘−x/2D180∘−x - Question 2 - Select One
In the adjoining figure BD is the diameter of the circle and ∠BCA=41∘. Find ∠ABD:
 A41∘B49∘C22.5∘D20.5∘
A41∘B49∘C22.5∘D20.5∘ - Question 3 - Select One
AB is a diameter of the circle with centre O and chord CD is equal to radius OC (fig). AC and BD proudced meet at P. Prove that ∠CPD=60∘.
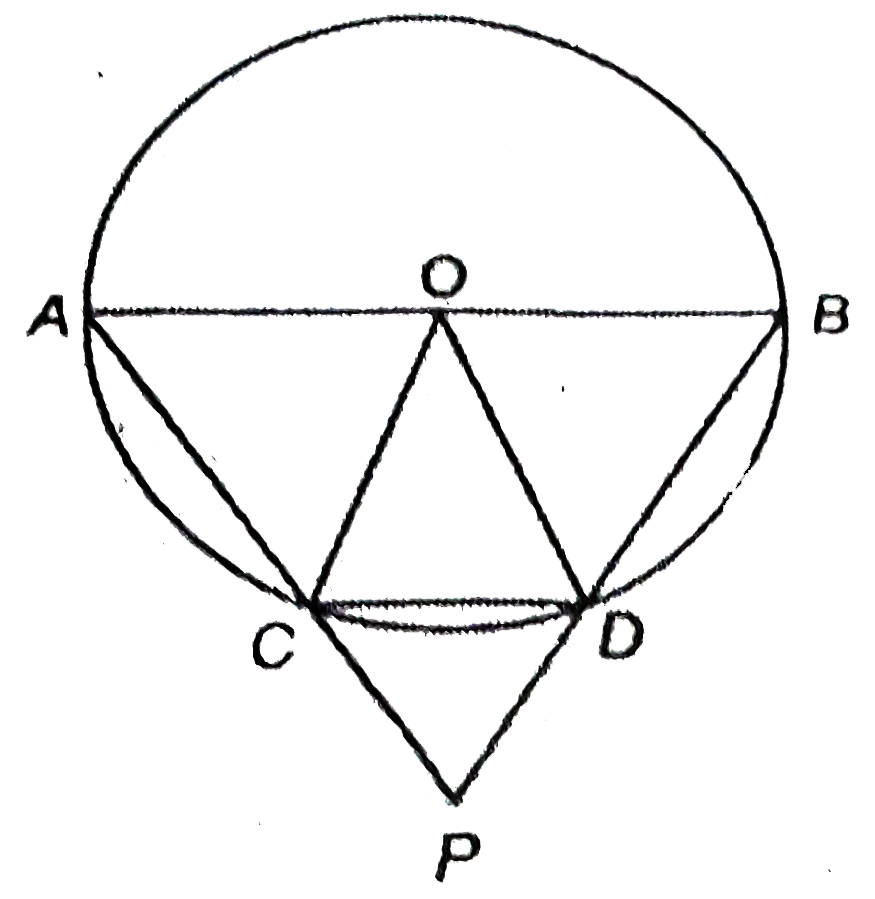 A60∘B30∘C90∘D160∘
A60∘B30∘C90∘D160∘
In the given figure, prove that AC=BD.
 View Solution
View SolutionIn the adjoinig figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘.
 View Solution
View SolutionIn the adjoining figure, seg AB is a diameter of a circle with centre O. the bisector of ∠ACB intersects the circle at point D. Prove that ,seg AD≅segBD. Complete the following proof by filling the blanks.
 View Solution
View SolutionIn the adjoining figure, O is the centre of the circle and AC is its diameter. If ∠BAC=30∘, then find ∠BOC.
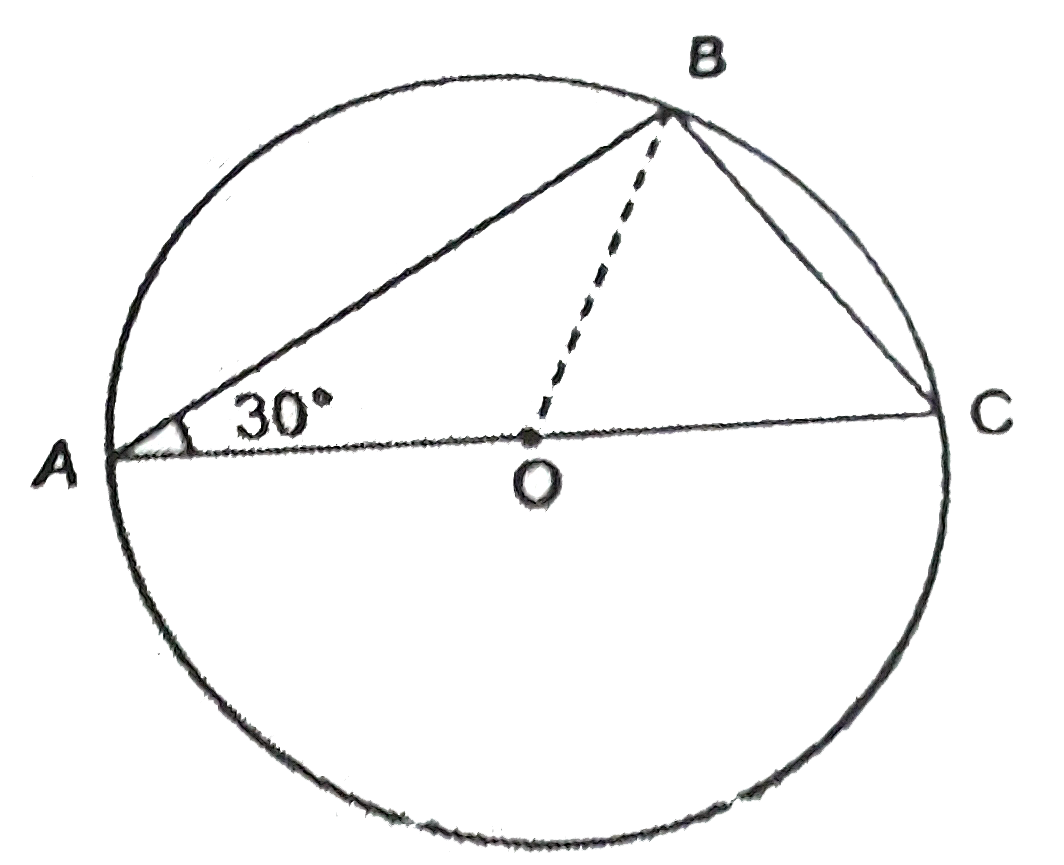 View Solution
View SolutionIn a class of 39 students the ratio of boys and girls is 2 : 1. Radhika ranks 15th among all the students from top and 8th among girls from bottom. How many boys are there below Radhika ?
View Solution



