Δ ABC is an isosceles triangle in which AB=AC. If D and E are midpoints of AB and AC respectively, prove that the points B,C,E and D are concyclic.
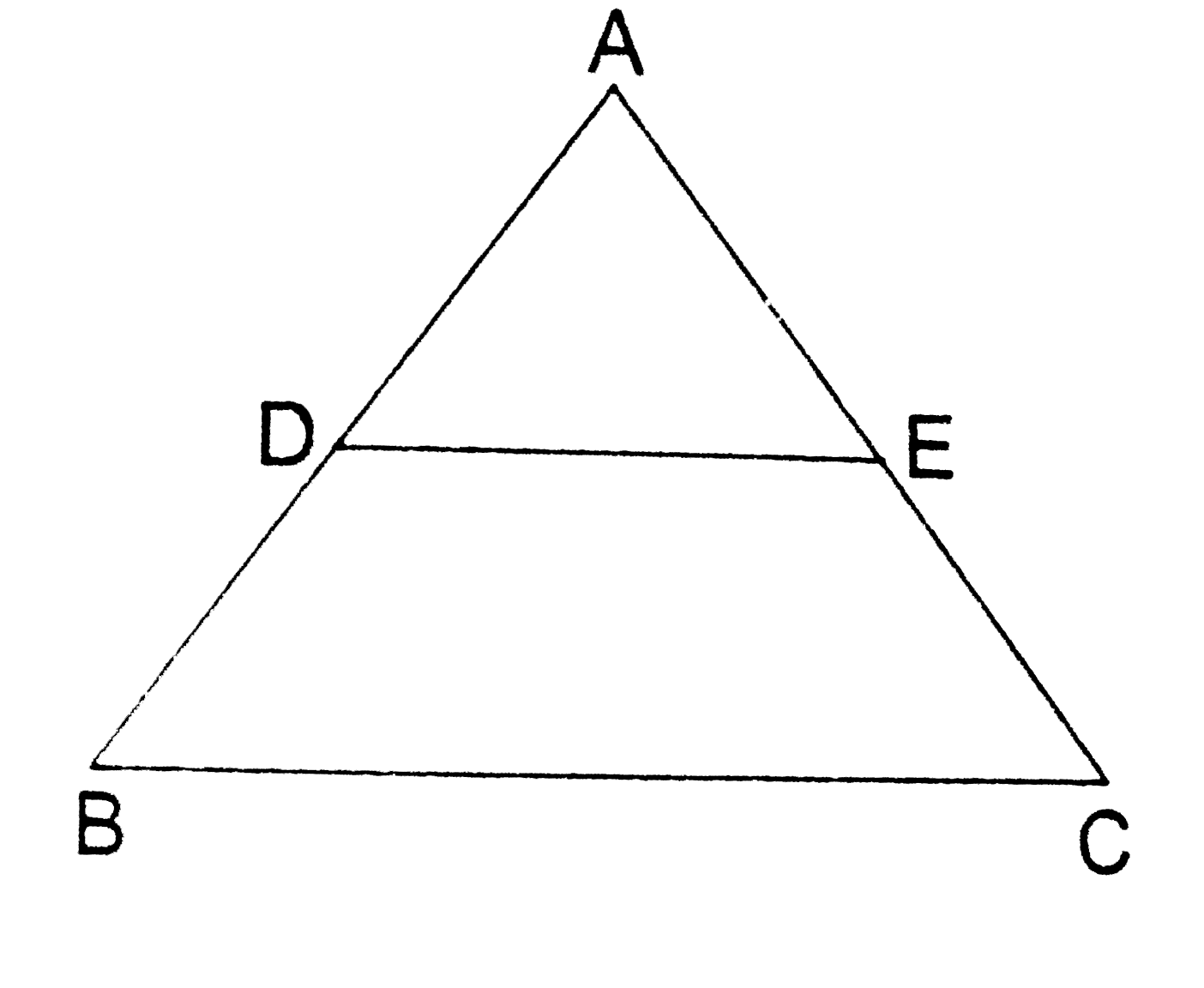
In order to show that the points B,C,E and D are concyclic, we must prove that ∠ECB+∠EDB=180∘
Since D and E are the midpoints of AB and AC respectively, we have DE∣∣BC.
Now,DE∣∣BC
⇒∠ABC=∠ADE
⇒∠ACE=∠ADE ....(i) [∵AB=AC⇒∠ABC=∠ACB].
∴∠ECB+∠EDB=∠ACB+∠EDB
=∠ADE+∠EDB [ using (i) ]
=180∘
[∵∠ADE and ∠EDB form a linear pair ]
Hence, the points B,C,E and D are concyclic
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Exercise 12A22videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12B18videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B16videos
BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGON
- BOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)20videos
CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLE
Similar Questions
ABC is an isosceles triangle in which AB=AC. If D and E are the mid-points of AB and AC respectively, prove that the points B, C, D and E are concyclic.
View SolutionABC is an isosceles triangle in which AB=AC. If DandE are the mid-points of ABandAC respectively, prove that the points B,C,DandE are concylic.
View Solution
Knowledge Check
- Question 1 - Select One
In the adjoining figure, ABC is an isosceles triangle in which AB = AC. If E and F be the midpoints of AC and AB respectively, then
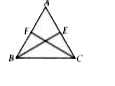 ABE = CFB∠BFC=∠CEBCBF = CEDAll of these
ABE = CFB∠BFC=∠CEBCBF = CEDAll of these - Question 2 - Select One
In the adjoining figure, ABC is an isosceles triangle in which AB=AC. If E and F be the midpoints of AC and AB respectively, then
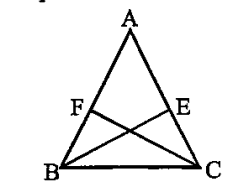 ABE=CFB∠BFC=∠CEBCBF=CEDAll of these
ABE=CFB∠BFC=∠CEBCBF=CEDAll of these - Question 3 - Select One
If in a triangle AB=a,AC=b and D,E are the mid-points of AB and AC respectively, then DE is equal to
Aa4−b4Ba2−b2Cb4−a4Db2−a2
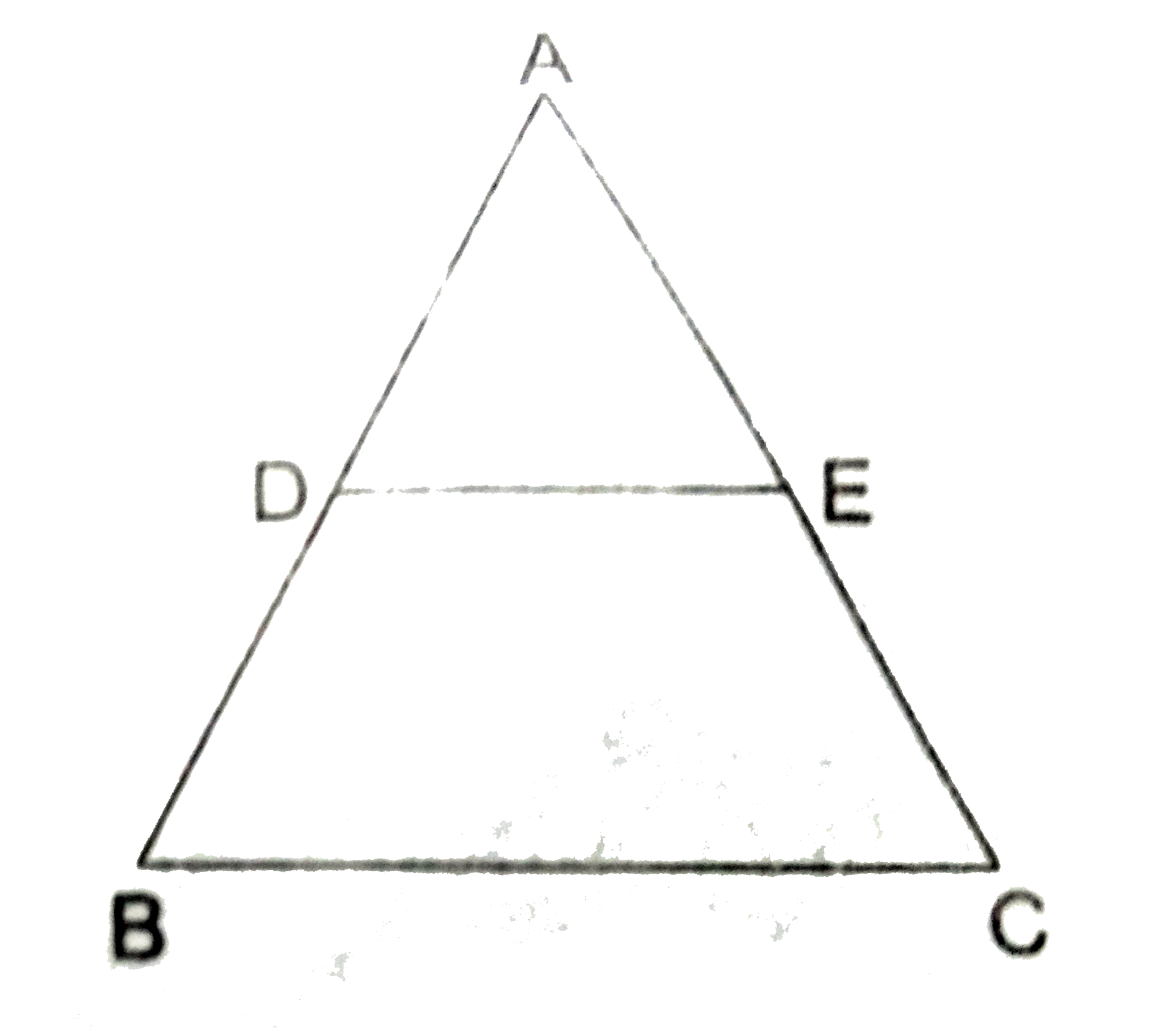
In the adjoining figure, ABC is a triangle in whcich AB=AC. If D and E are poitns on AB and AC respecrtively such that AD=AE, show that the points B,C,E and D are concyclic.
 View Solution
View SolutionIn Figure, ABC is a triangle in which AB=AC. Point DandE are points onthe sides ABandAC respectively such that AD=AE. Show that the points B,C,EandD are concyclic.
View SolutionABC is a triangle in which AB=AC.DandE are points on the sides ABandAC respectively, such that AD=AE. Show that the points B<C<EandD are concyclie.
View SolutionIf in a triangle ABC and D, E are the mid-points of AB and AC respectively, then →DE is equal to
View SolutionLet ABC be an isosceles triangle with AB=AC and let D,E,F be the mid-points of BC,CA and AB respectively. Show that AD⊥FE and AD is bisected by FE.
"
View Solution

