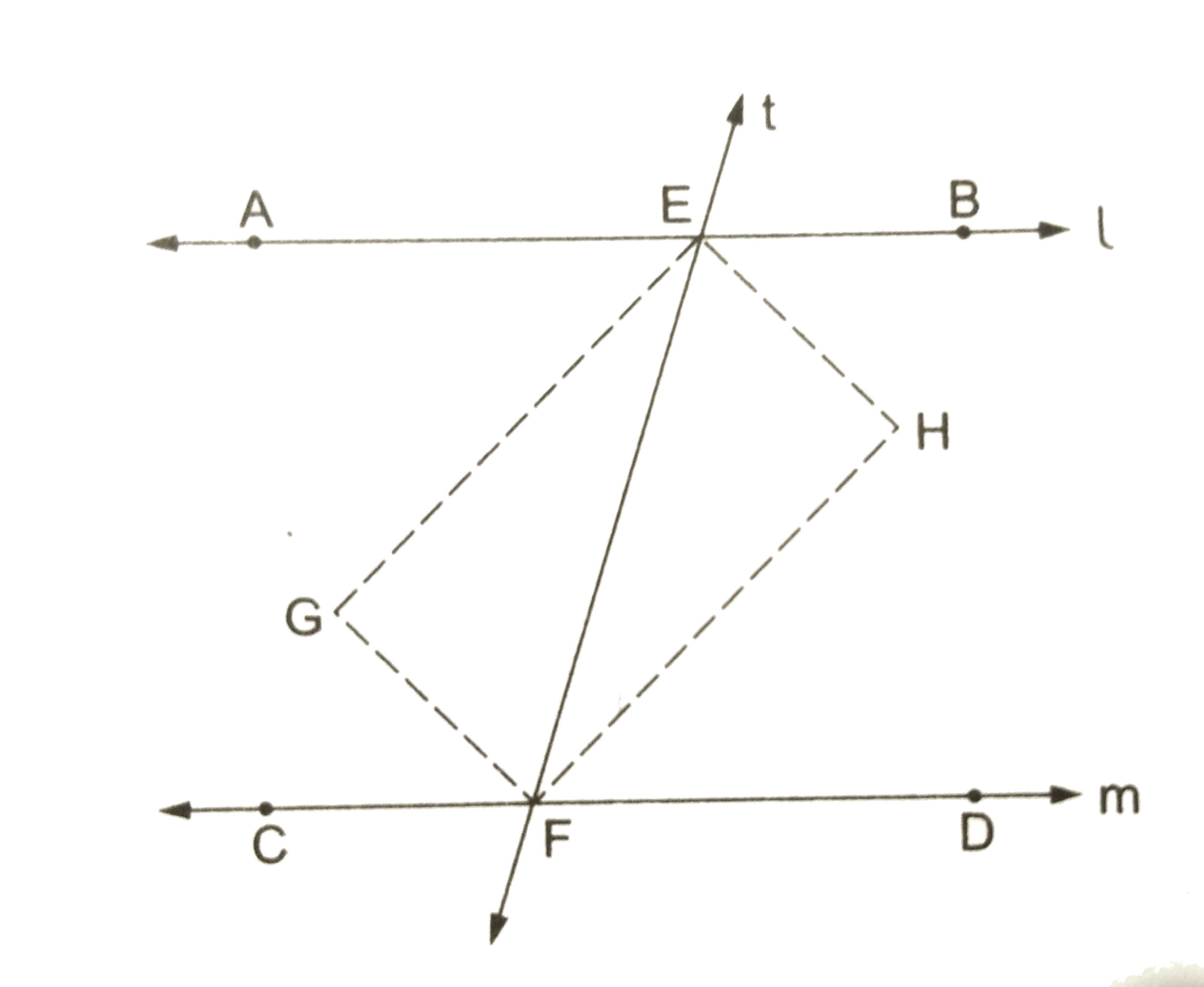
Two parallel lines l and m are intersected by a transversal p (see Fig. 8.15). Show that the quadrilateral formed by the bisectors of interior angles is a rectangle.
∠AEF+∠BEF=180∘ (linear pair)
⇒12(∠AEF)+12(∠BEF)=90∘
⇒∠GEF+∠FEH=90∘⇒∠GEH=90∘.
Now, ∠AEF+∠CFE=180∘ (co-interior ∠)
⇒12(∠AEF)+12(∠CFE)=90∘
⇒∠GEF+∠GFE=90∘⇒∠EGF=90∘
(sum of ∠ of a △ is 180∘).
Similarly, ∠GFH=∠EHF=90∘.
Similar Questions
Knowledge Check
Two parallel line l and m are intersected by a transversal p. The quadrilateral formed by the bisectors of interior angles is a
ATrapeziumBKiteCParallelogramDSquareTwo parallel lines AB and CD are intersected by a transversal EF at M and N respectively.
The lines MP and NP are the bisectors of interior angles ∠BMN and ∠DNM on the same side of the transversal. Then ∠MPN is equal to :A60∘B90∘C45∘D120∘Two parallel lines AB and CD are intersected by a transversal EF at M and N respectively.
The lines MP and NP are the bisectors of interior angles ∠BMN and ∠DNM on the same side of the transversal. Then ∠MPN is equal to :A60∘B90∘C45∘D120∘
If two parallel lines are intersected by a transversal, prove that the bisectors of the two pairs of interior angles enclose a rectangle.
View SolutionIf two parallel lines intersected by a transversal; prove that the bisectors of the two pairs of interior angle encloses a rectangle.
View SolutionTwo parallel lines AB and CD are intersected by a transversal line EF at M and N, respectively. If the lines MP and NP are the bisectors of the interior angles BMN and DNM on the same side of the transversal, then ∠MPN is equal to
View SolutionTwo parallel lines AB and CD are intersected by a transversal line EF at M and N, respectively. If the lines MP and NP are the bisectors of the interior angles BMN and DNM on the same side of the transversal, then ∠MPN is equal to
View SolutionIf two parallel lines are intersected by a transversal , then the interior angles on the same side of the transversal are -
View Solution