A △ABC is given. If lines are drawn through A, B, C, parallel respectively to the sides BC, CA and AB, forming △PQR, as shown in the adjoining figure, show that BC=12QR.
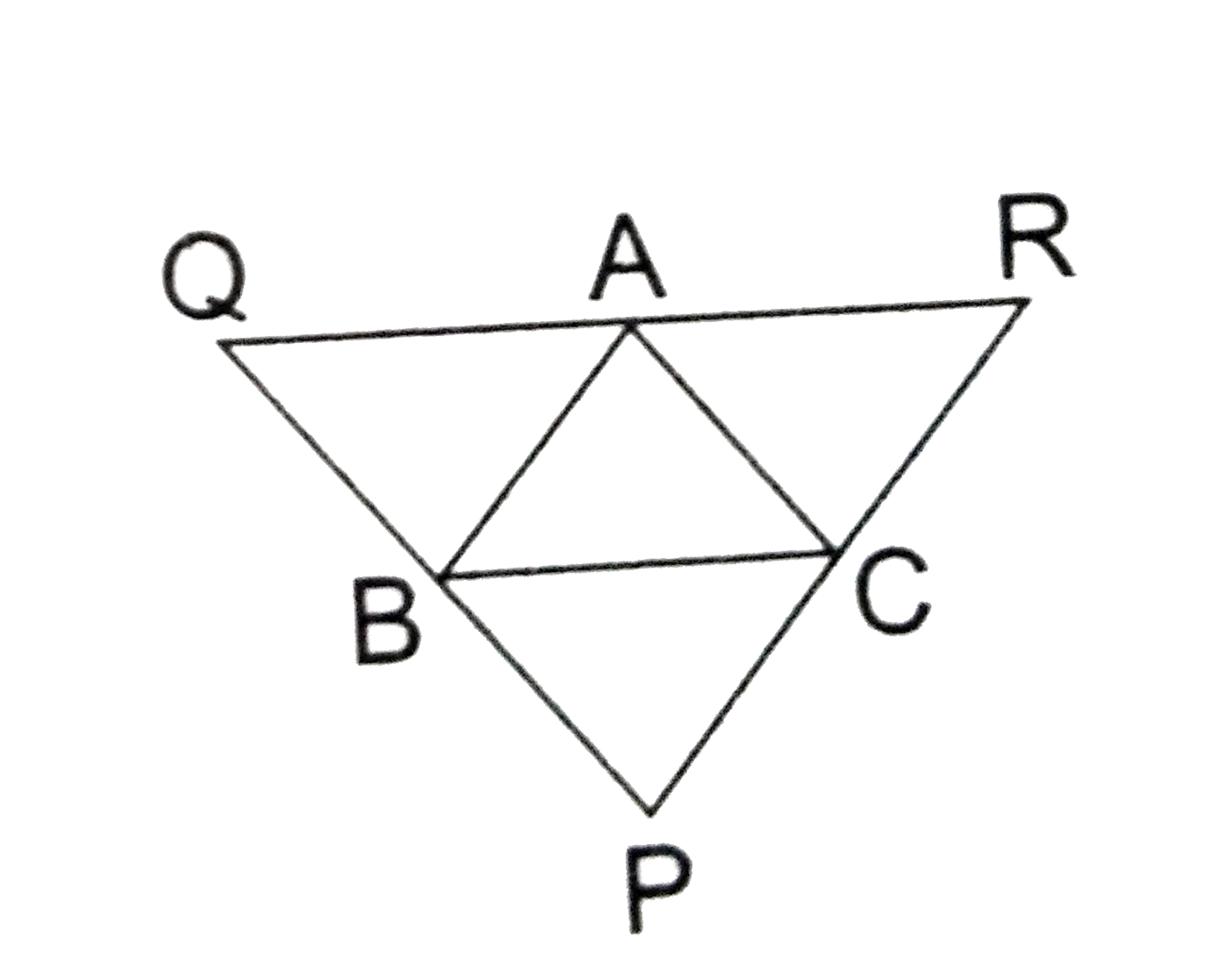
BC||QA and CA||QB ⇒BCAQ is a ||gm ⇒BC=QA.
Similarly, BCRA is a ||gm ⇒BC=AR.
∴2BC=QA+AR=QR.
Topper's Solved these Questions
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - EXERCISE 10C
18 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)
47 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Exercise 10 A
10 Videos
- PROBABILITYBOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
10 Videos
Similar Questions
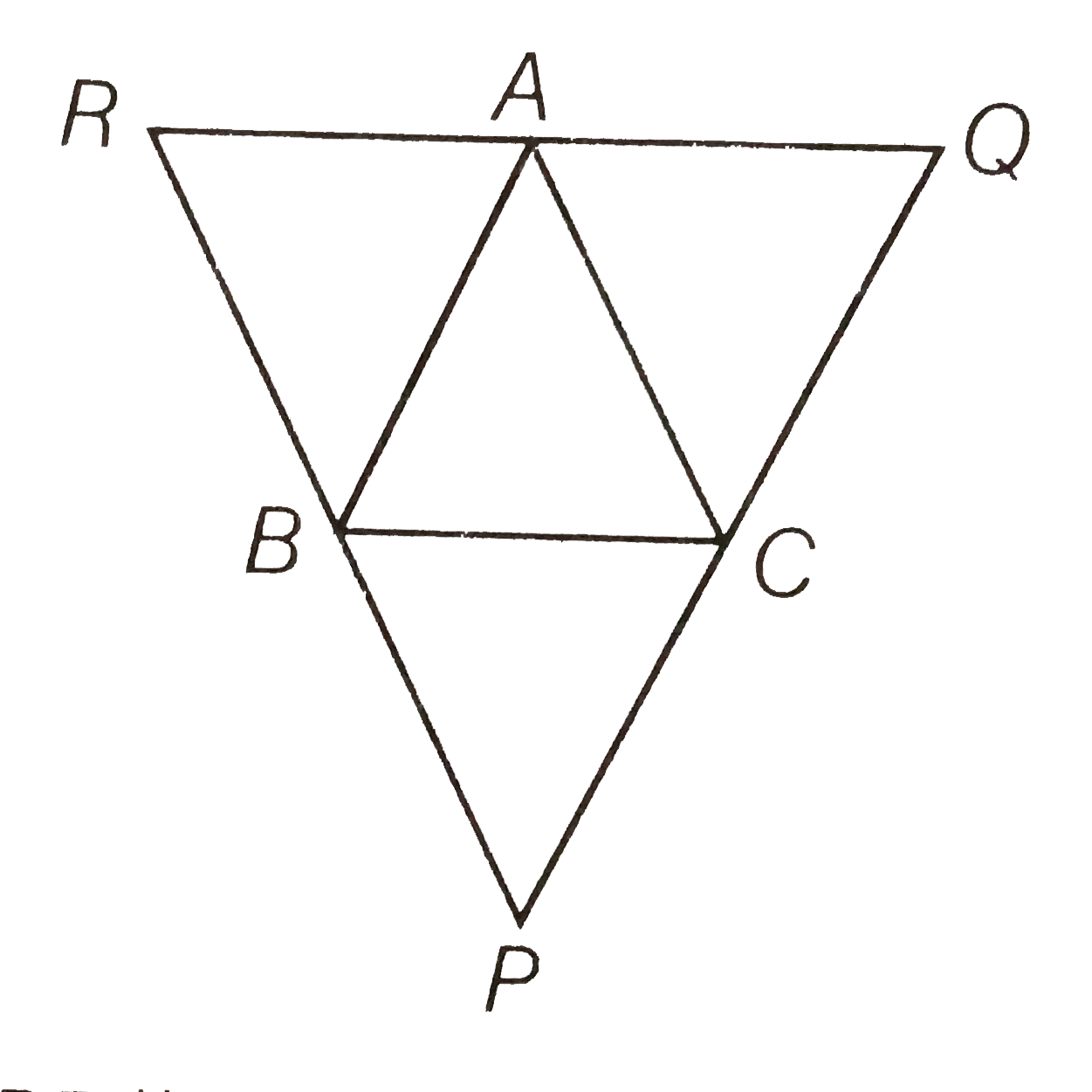
Given ΔABC, lines are drawn through A,BandC parallel respectively to thesides BC,CAandAB, forming ΔPQR (Fig. 13.27). Show that BC=12QR.
View SolutionThrough A, B and C lines RQ, PR and QP have been drawn, respectively parallel to sides BC, CA and AB of a ΔABC as shown in figure. Show that BC=12QR.
View Solution
Knowledge Check
Let →a,→b,→c form sides BC,CA and AB respectively of a triangle ABC then
Aa.b+b.c+c.a=0Ba×b=b×c=c×aCa.b=b.c=c.aDa×b+b×c+c×a=0In a triangle ABC, D, E, F are the mid-points of the sides BC, CA and AB respectively , the vector →AD is equal to
A→BE+→CFB→BE−→CFC→CF−→BED−→BE−→CF
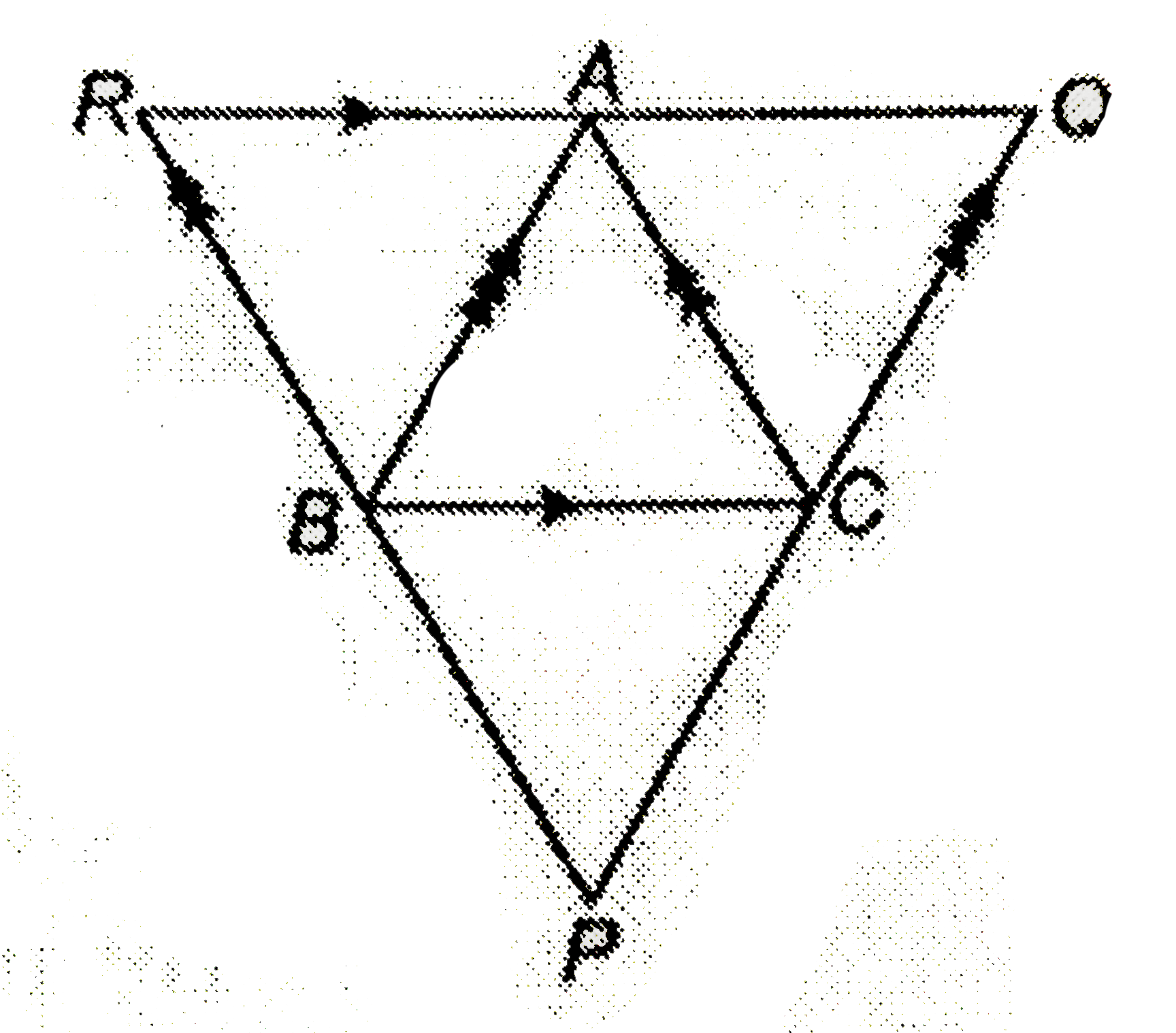
Throuth A,B and C lines RQ, PR and QP have been drawn, respectively parallel to sides BC. CA and AB of a ΔABC as shown in the given figure. Show that BC=12QR.
View SolutionD, E and F are the mid-points of the sides BC, CA and AB of a triangle ABC. Show that
BDEF is a parallelogram
View SolutionIn ΔABC the lines are drawn parallel to BC,CA and AB respectively through A,B and C intersecting at P, Q and R. Find the ration of perimeter of ΔPQR and ΔABC
View SolutionLet →a,→b,→c form sides BC,CA and AB respectively of a triangle ABC then
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, AC and AB respectively. △DEF is congruent to triangle :

View SolutionIn the adjoining figure D, E and F are the mid - points of the sides BC, AC and AB respectively to triangle. Show that ∠EDF=∠A, ∠DEF=∠B and ∠DFE=∠C:

View Solution
