In the adjoining figure, △ABC is a triangle and through A, B, C lines drawn, parallel respectively to BC, CA and AB, intersecting at P, Q and R. Prove that the perimeter of △PQR is double the perimeter of △ABC.
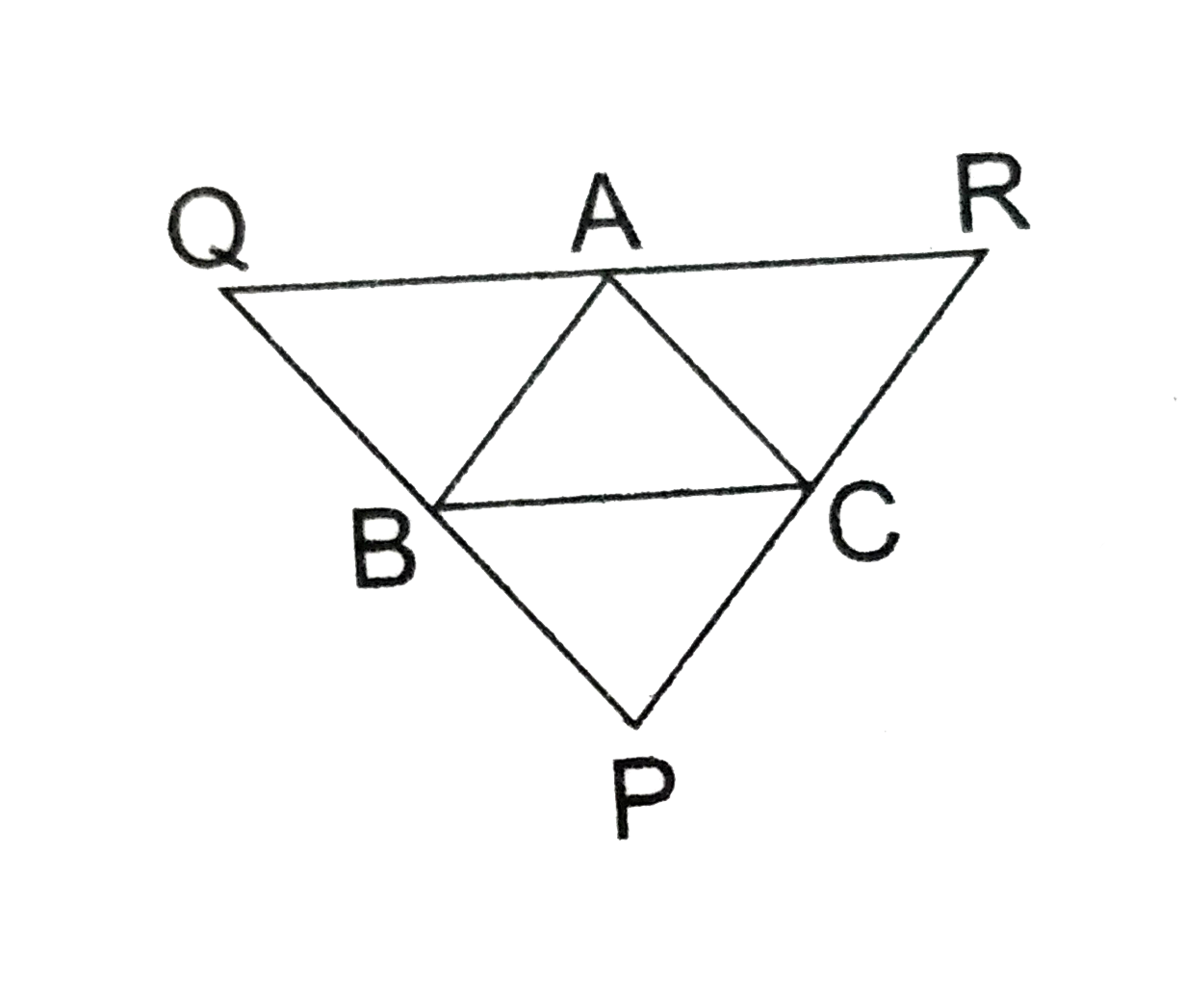
As poved in prev. questions: BC=12QR,CA=12PQ,AB=12PR
⇒AB+BC+CA=12(PR+QR+PQ).
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - EXERCISE 10C18videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)47videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Exercise 10 A10videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)16videos
PROBABILITY
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)10videos
TRIANGLES
Similar Questions
ABC is a triangle and through A, B, C lines are drawn parallel to BC, CA and AB respectively intersecting at P, Q and R . Prove that the perimeter of PQR is double the perimeter of ABC
View SolutionIn ΔABC the lines are drawn parallel to BC,CA and AB respectively through A,B and C intersecting at P, Q and R. Find the ration of perimeter of ΔPQR and ΔABC
View Solution
Knowledge Check
- Question 1 - Select One
In △ABC and △ DEF, AB = DE, BC = EF and ∠B=∠E. If the perimeter of △ ABC is 20, then the perimeter of △ DEF is ..........
A10B20C15D40 - Question 2 - Select One
If D, E and F are the mid-points of sides BC, CA and AB respectively of △ABC, then the ratio of the areas of △DEF to the area of △ABC is :
A1:4B1:2C1:3D2:3 - Question 3 - Select One
In an Isosceles Δ ABC, AB = AC, the altitude of the triangle is 12 cm and the perimeter of the triangle is 36 cm. Find the length of side BC.
A12 cmB10 cmC8 cmD9 cm
Given ΔABC, lines are drawn through A,BandC parallel respectively to thesides BC,CAandAB, forming ΔPQR (Fig. 13.27). Show that BC=12QR.
View SolutionABC is a triangle A line is drawn parallel to BC to meet AB and AC in D and E respectively. Prove that the median through A bisects DE.
View SolutionIn △ ABC, the bisectors of ∠B and ∠ C intersect at I. A line drawn through I and parallel to BC intersects AB at P and AC at Q. Prove that PQ = BP + CQ.
View SolutionIn A ΔABC,AD,BEandCF are three medians . The perimeter of ΔABC is always
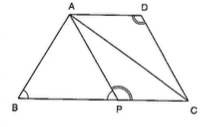
View SolutionP is a point on the side BC of a triangle ABC such that AB=AP. Through AandC, lines are drawn parallel to BCandPA, respectively, so as to intersect at D as shown in Figure. Show that ABCD is a cyclic quadrilateral.
 View Solution
View Solution

