In the adjoining figure, ABCD is a parallelogram. Points P and Q on BC trisect BC. Prove that
ar(△APQ)=ar(△DPQ)=16ar(△ABCD).

Through P and Q, we draw PM and QN parallel to AB. Parallelograms ABPM, MPQN and NQCD have equal areas since they have equal bases and lie between the same parallels [ Theorem 3].

∴ar(||gm ABPM)=ar(||gm MPQN)
=ar(||gm NQCD)=13ar(||gm ABCD)....(i)
Now, ar(△APQ)=ar(△DPQ)
=12ar(||gm MPQN)
[∴△APQ,triantg≤DPQ and "||gm" MPQN have the same base PQ and lie between the same parallels AD and BC]
⇒ar(△APQ)=ar(△DPQ)=12{13ar(||gm ABCD)} [using (i)].
Hence, ar(△APQ)=ar(△DPQ)=16ar(||gm ABCD).
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - Exercise 1138videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)32videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)16videos
AREAS OF TRIANGLES AND QUADRILATERALS
Similar Questions
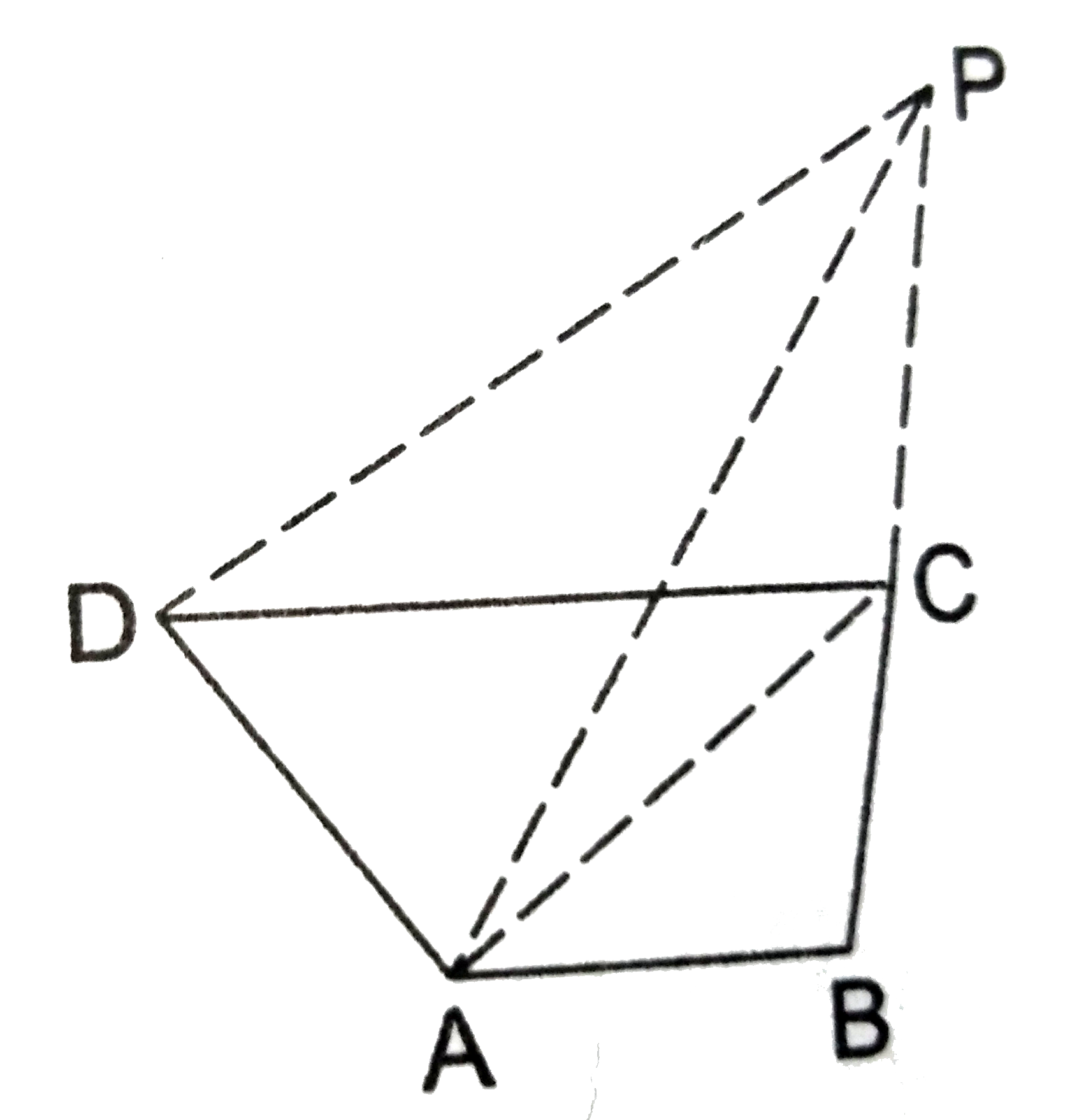
In the adjoining figure, ABCD is a parallelogram and P is any points on BC. Prove that
ar(△ABP)+ar(△DPC)=ar(△PDA).
 View Solution
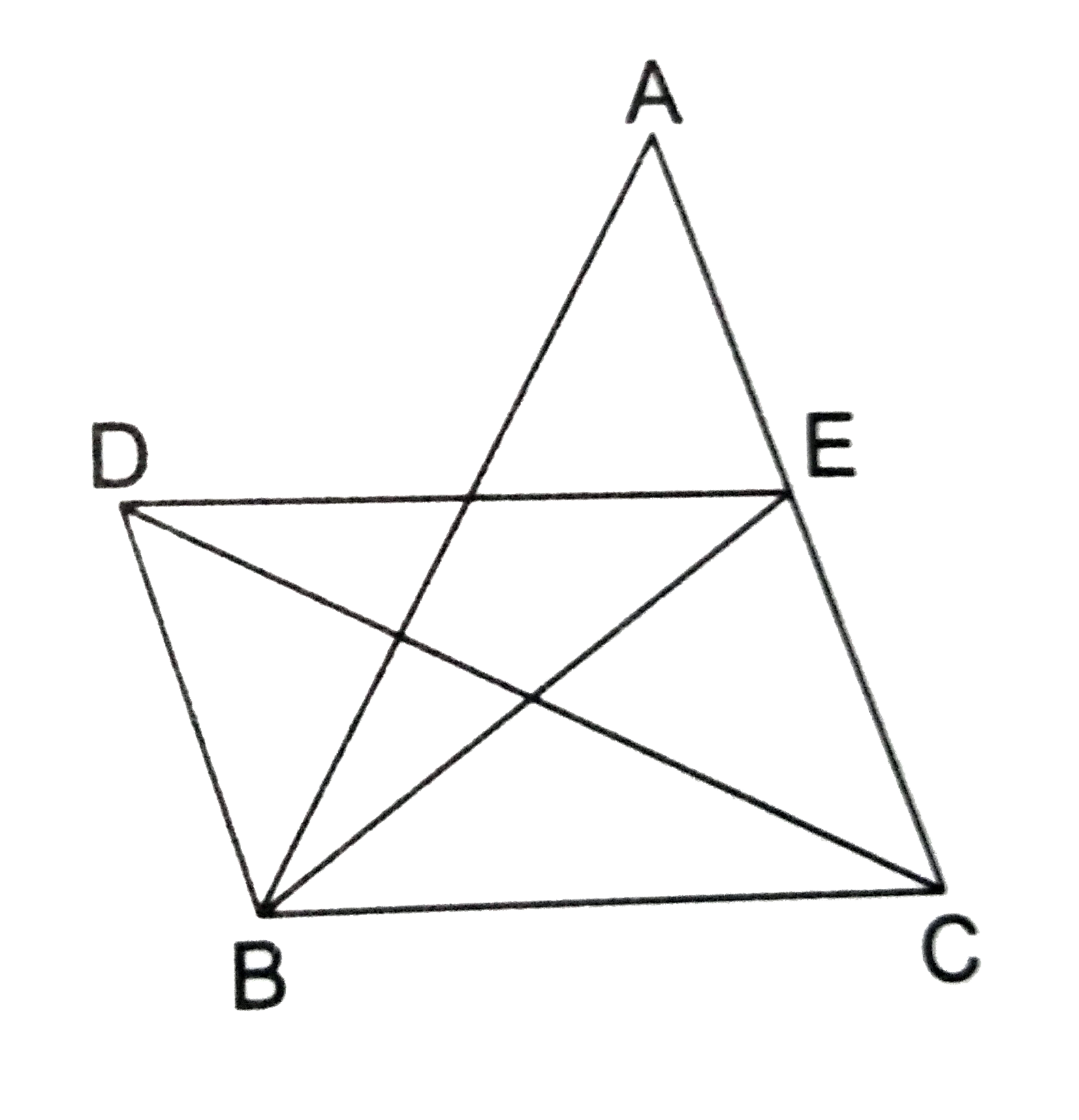
View SolutionIn the given figure, ABCD is a parallelogram. E and F are any two points on AB and BC, respectively. Prove that ar(△ADF)=ar(△DCE).
View SolutionIn the adjoining figure, BD||CA, E is the midpoint of CA and BD=12CA. Prove that
ar(△ABC)=2ar(△DBC).
 View Solution
View SolutionABCD is a parallelogram. X and Y are mid-points of BC and CD. Prove that ar(△AXY)=38ar(∣∣gmABCD)
View SolutionIn the adjoining figure, MNPQ and ABPQ are parallelogram and T is any point on the side BP. Prove that
(i) ar(MNPQ)=ar(ABPQ)
(ii)ar(△ATQ)=12ar(MNPQ).
 View Solution
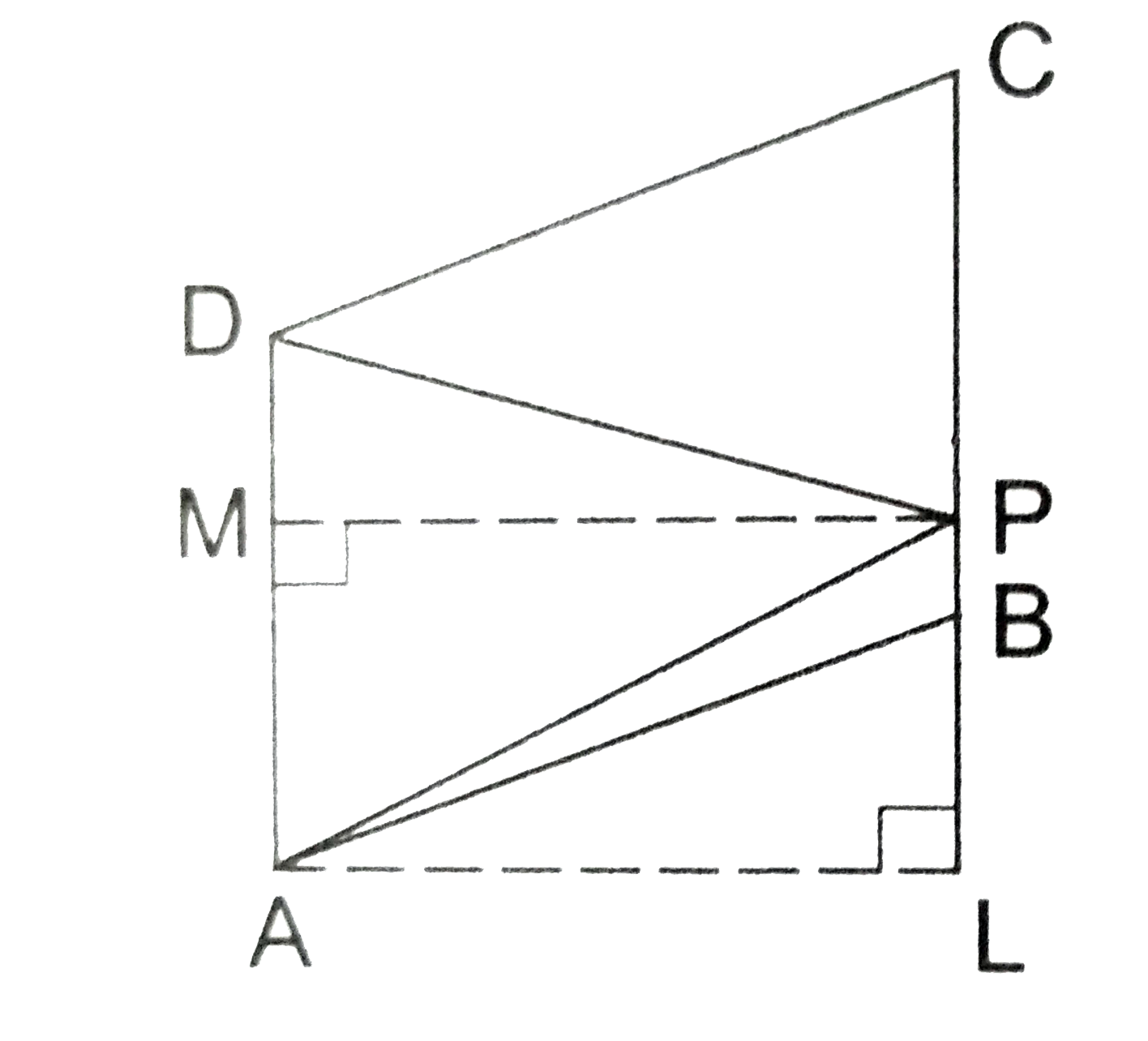
View SolutionIn the adjoining figure, ABCD is a quadrilateral. A line through D, parallel to AC, meets BC produced in P .
Prove that ar(△ABP)=ar(qaud. ABCD).
 View Solution
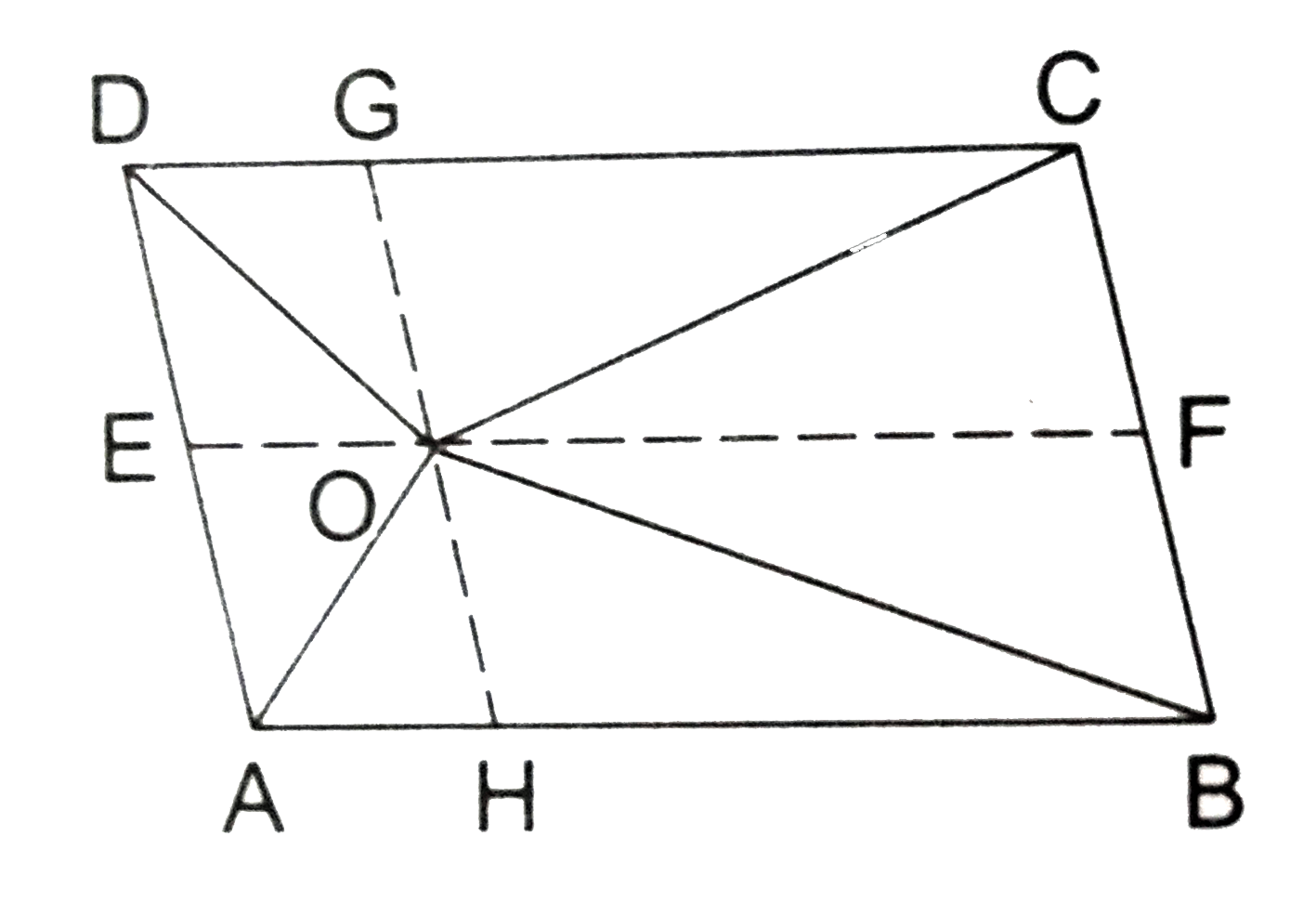
View SolutionABCD is a parallelogram and O is a point in its interior. Prove that
(i) ar(△AOB)+ar(△COD)
=12ar(||gm ABCD).
(ii) ar(△AOB)+ar(△COD)=ar(△AOD)+ar(△BOC).
 View Solution
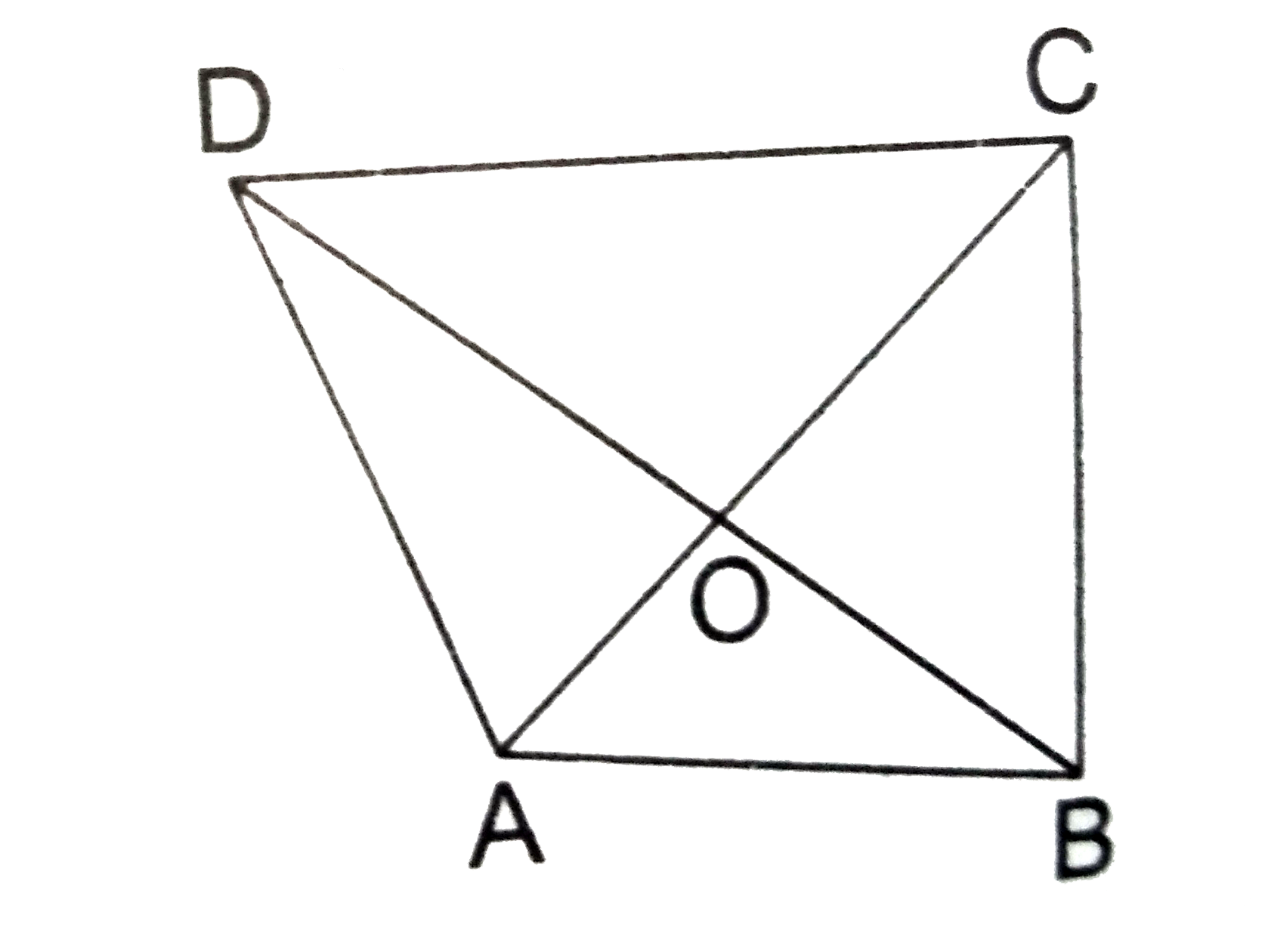
View SolutionIn the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect at O.
If BO=OD, prove that
ar(△ABC)=ar(△ADC).
 View Solution
View SolutionP is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(△APD) = ar(△CPD).
View SolutionABC is a triangle in which D is the midpoint of BC and E is the midpoint of AD.
Prove that ar(△BED)=14ar(△ABC).
 View Solution
View Solution

