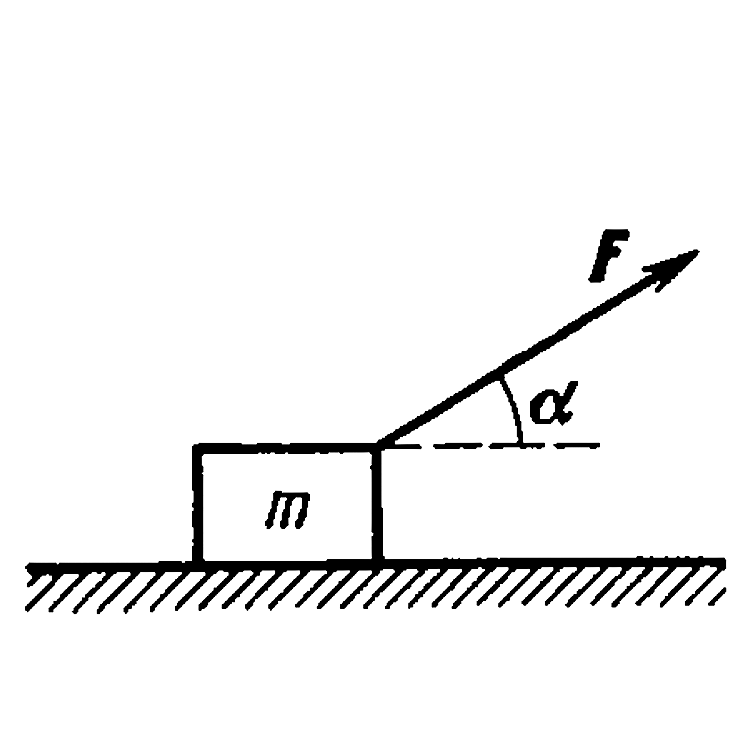
A body of mass m resting on a smooth horizontal plane starts moving under a constant force F. During its rectilinear motion, the angle θ between the direction of force and horizontal plane varies as 8 = kx , where k is a constant and x is the distance travelled by the body from the initial position. What is the velocity of the body?
2Fmtanθ
√2FsinθmK
√Fcosθmk
√2Fcosθmk
The correct Answer is:B
Topper's Solved these Questions
- NEWTONS LAWS OF MOTION BOOK - AAKASH SERIESCHAPTER - NEWTONS LAWS OF MOTION EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II (LECTURE SHEET (ADVANCED)) (More than one correct answer Type Questions )
2 Videos
- NEWTONS LAWS OF MOTION BOOK - AAKASH SERIESCHAPTER - NEWTONS LAWS OF MOTION EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II (LECTURE SHEET (ADVANCED)) (Linked Comprehension Type Questions)
2 Videos
- NEWTONS LAWS OF MOTION BOOK - AAKASH SERIESCHAPTER - NEWTONS LAWS OF MOTION EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - I (MAIN)) (Straight Objective Type Questions)
26 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Questions for Descriptive Answers
7 Videos
- OSCILLATIONBOOK - AAKASH SERIESCHAPTER - OSCILLATIONEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
12 Videos
Similar Questions
A bar of mass m resting on a smooth horizontal plane starts moving due to the force F=mg/3 of constant magnitude. In the process of its rectilinear motion the angle α between the direction of this force and the horizontal varies as α=as, where a is a constant, and s is the distance traversed by the bar from its initial position. Find the velocity of the bar as a function of the angle α.
View SolutionA bar of mass m resting on a smooth horizontal plane starts moving due to the force F=mg/3 of constant magnitude. In the process of its rectilinear motion the angle α between the direction of this force and the horizontal varies as α=as, where a is a constant, and s is the distance traversed by the bar from its initial position. Find the velocity of the bar as a function of the angle α.
View Solution
Knowledge Check
A body which was released from rest, slides down on an inclined plane of inclination θ. The coefficient of friction dowh the plane varies as μ=kx where k is a spositive constant and x is the distance moved by the body down the plane. The speed of the body 'v' versus distance 'x' graph will be as :
A B
B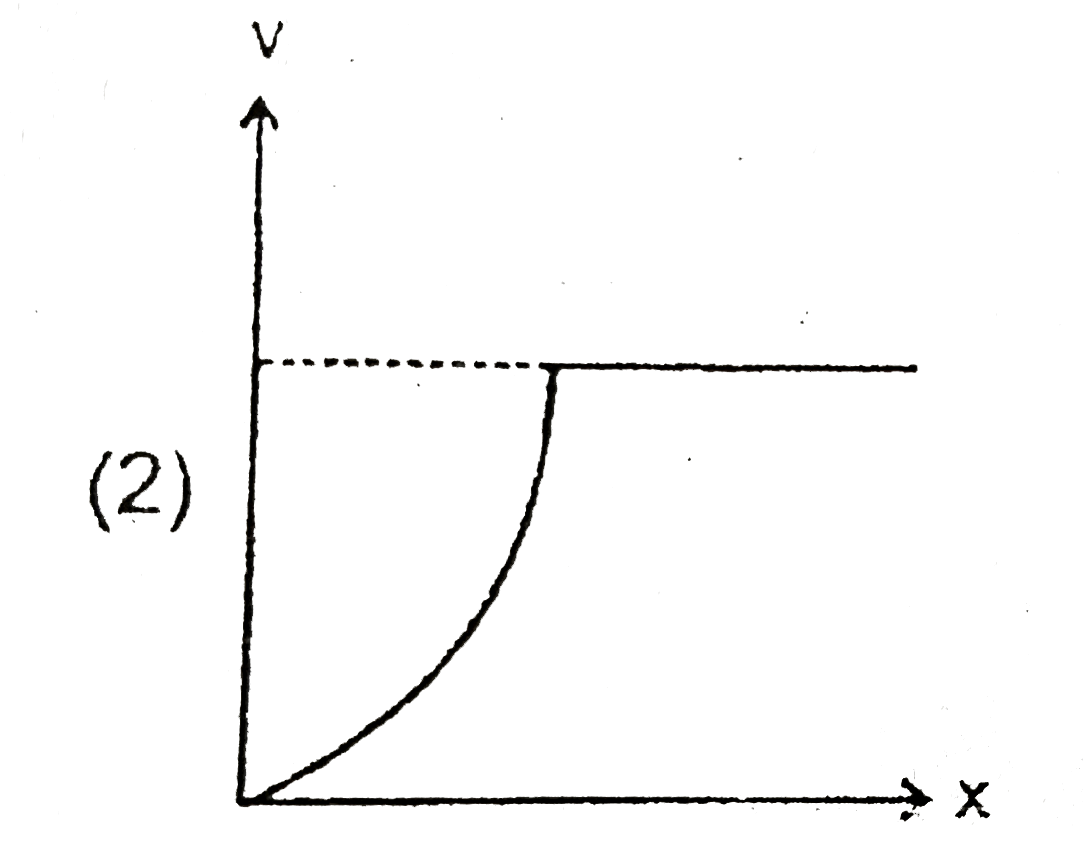 C
C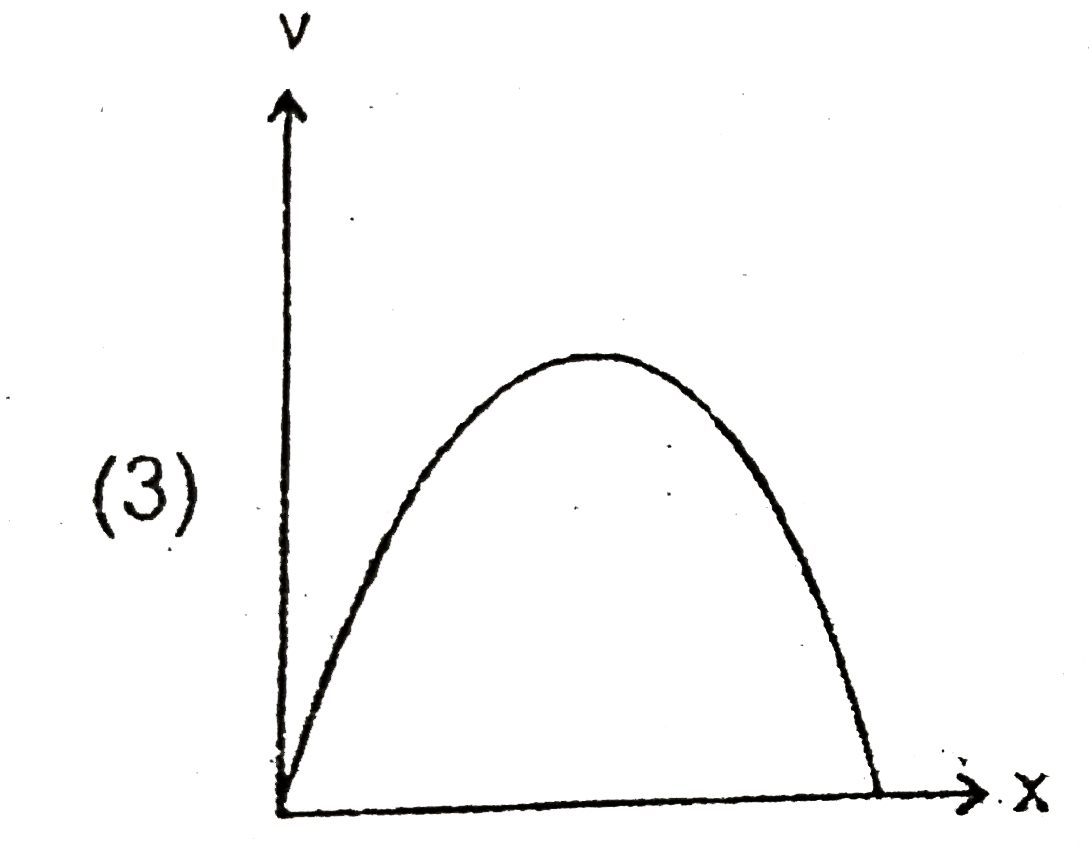 D
D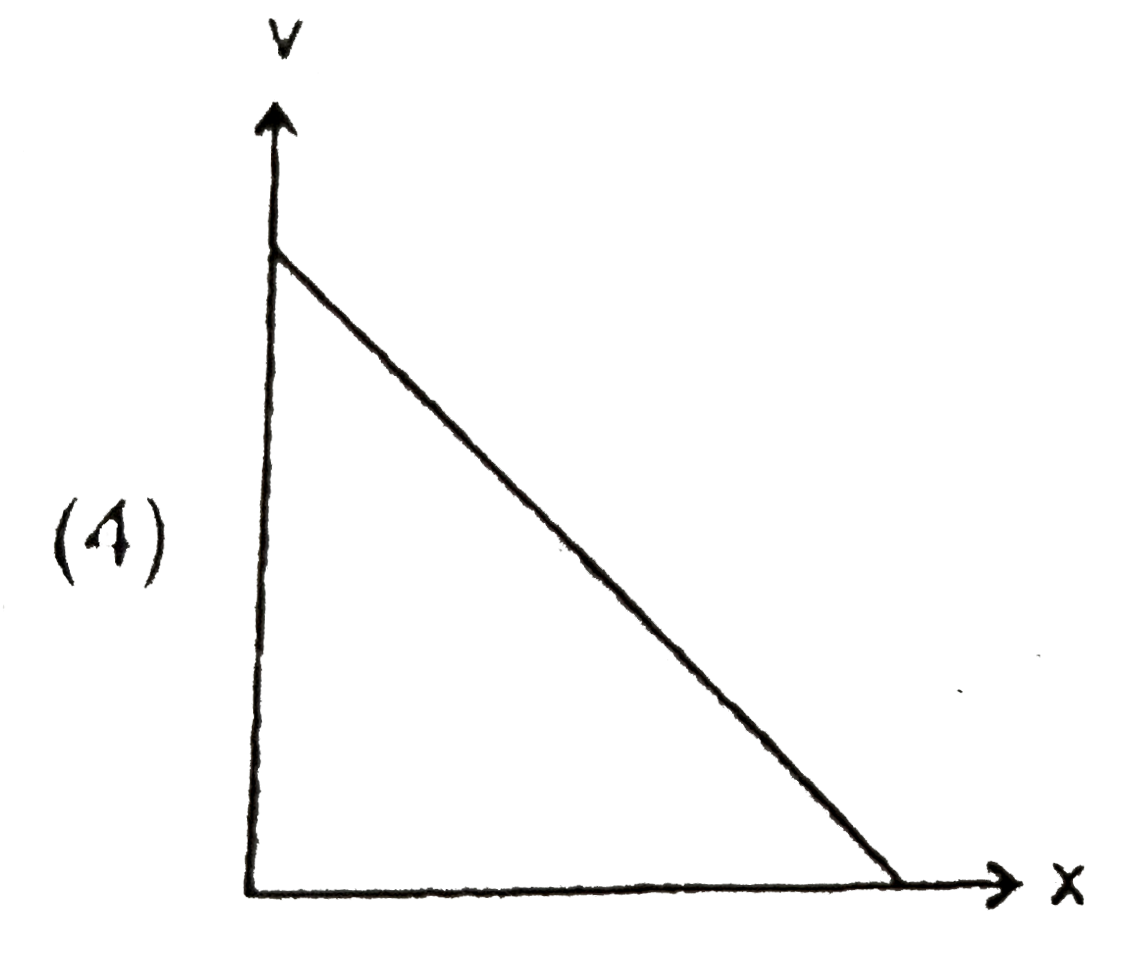
A body of mass M is resting on a rough horizontal plane surface the coefficient of friction being equal to μ At t=0 a horizontal force F=F0t starts acting on it , where F0 is a constant find the time T at which the motion starts?
AμMg/F0Bmg/μF0CμF0MgDNone of these
A block of mass m resting on a smooth horizontal plane starts moving due to a constant force F=mg/3 of constant magnitude. In the process of its rectilinear motion the angle θ varies as θ=λs, where λ is constant and s is the distance traversed by the block from its intial position. Find the velocity of the block as a function of the angle θ. Also show that the block will never lose contact with the ground.
View SolutionA body of mass m rests on a horizontal plane with the friction coefficient k. At the moment t=0 a horizontal force is applied to it, which varies with time as F=at, where a is a constant vector.
Find the distance traversed by the body during the first t seconds after the force action began.
View SolutionAt the moment t = 0 , the force F = kt is applied to a small body of mass 'm' resting on a smoth horizontal plane. (K is a positive constant ). The direction of the force an angle θ with the horizontal always as shown

The distance travelled x by the body along horizontal before it leaves contact with the horizontal at t=t0 can be expressed in relation with time 't' as
View SolutionAt the moment t=0 the force F=at is applied to a small body of mass m resting on a smooth horizontal plane (a is constant).
The permanent direction of this force forms an angle α with the horizontal (figure). Find:
(a) the velocity of the body at the moment of its breaking off the plane,
(b) the distance traversed by the body up to this moment.
View SolutionA body which was released from rest, slides down on an inclined plane of inclination θ. The coefficient of friction dowh the plane varies as μ=kx where k is a spositive constant and x is the distance moved by the body down the plane. The speed of the body 'v' versus distance 'x' graph will be as :
View SolutionA body is moving down a long inclined plane of angle of inclination 'θ' for which the coefficient of friction varies with distance x as μ(x) = kx , where k is a constant . Here x is the distance moved by the body down the plane . The net force on the body will be zero at a distance x0 is given by ..........
View Solution
