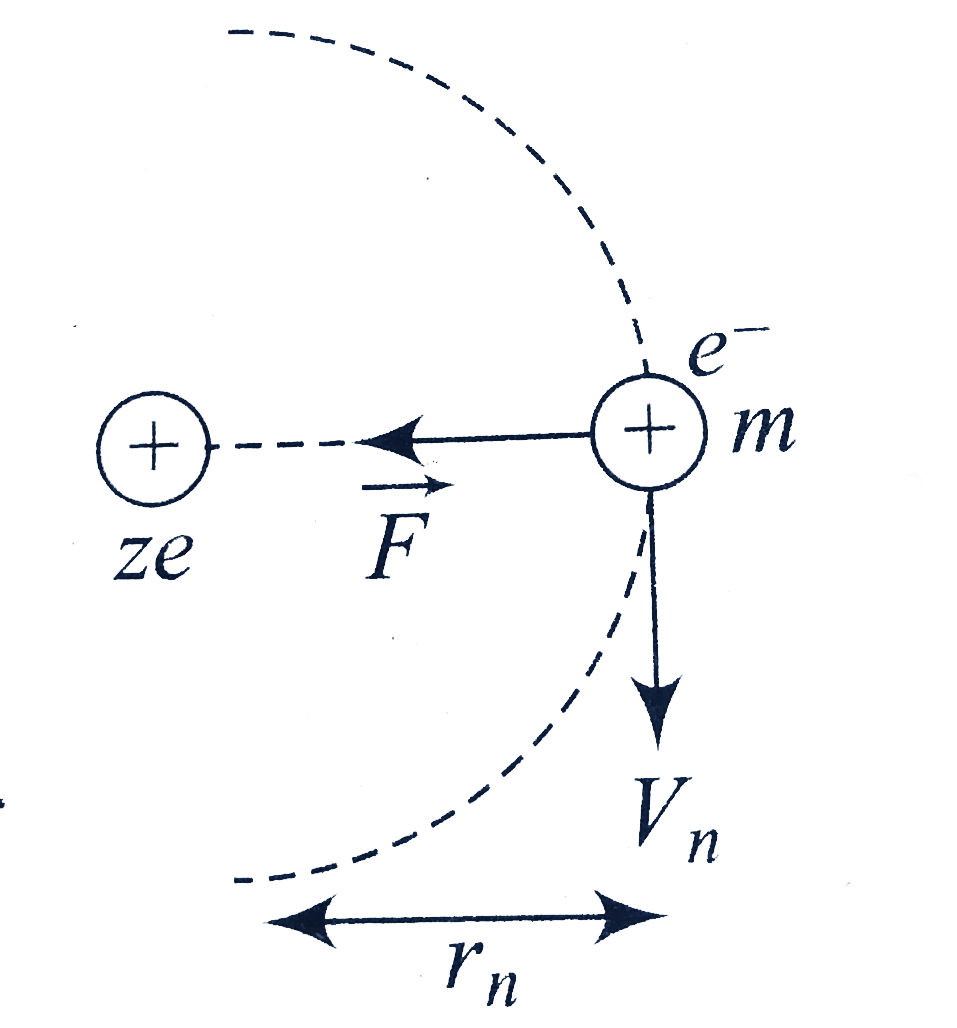
What are the dimensions of χ, the magnetic susceptibility? Consider an H-atom. Guess an expression for χ upto a constant by constructing a quantity of dimensions of χ, out of parameters of the atom: e, m, v, R and μ0. Here, m is the electronic mass, v is electronic velocity, R is Bohr radius. Estimate the number so obtained and compare with the value of ∣∣χ⌈10−5 for any solid material.
To solve the problem, we will follow these steps:
Step 1: Determine the dimensions of magnetic susceptibility (χ)
Magnetic susceptibility (χ) is defined as the ratio of magnetization (M) to the magnetic field strength (H):
χ=MH
Both magnetization (M) and magnetic field strength (H) have the same dimensions, which makes χ a dimensionless quantity. Thus, the dimensions of χ are:
Dimensions of χ=(χ)=1(dimensionless)
Step 2: Write down the known parameters and their dimensions
We need to construct a quantity with the dimensions of χ using the parameters: e (charge), m (mass of electron), v (velocity of electron), R (Bohr radius), and μ₀ (permeability of free space).
- Charge (e): (e) = (Q)
- Mass (m): (m) = (M)
- Velocity (v): (v) = (L)(T)⁻¹
- Bohr radius (R): (R) = (L)
- Permeability of free space (μ₀): (μ₀) = (M)(L)⁰(T)⁻²(Q)²
Step 3: Construct a formula for χ
We will express χ in terms of the parameters:
χ∼μ0e2mavbRc
where a, b, and c are constants we need to determine.
Step 4: Substitute dimensions into the equation
Substituting the dimensions into the equation gives:
Dimensions of χ=(μ0)(e2)(ma)(vb)(Rc)
This can be expressed as:
(M)(L)−2(T)0(Q)2⋅(M)a⋅(L)b(T)−b⋅(L)c
Combining these gives:
(M)1+a(L)−2+b+c(T)−b(Q)2
Step 5: Set up equations for dimensional analysis
Since χ is dimensionless, we set the powers of M, L, T, and Q to zero:
1. 1+a=0
2. −2+b+c=0
3. −b=0
4. 2=0 (not applicable since we don't have charge in the final expression)
From the third equation, we find b=0. Substituting b=0 into the second equation gives c=2. From the first equation, we find a=−1.
Step 6: Substitute back to find χ
Now substituting a, b, and c back into the expression for χ:
χ∼μ0e2mR
Step 7: Calculate the numerical value of χ
Substituting the known values:
- μ₀ = 4π×10−7T m/A
- e = 1.6×10−19C
- m = 9.1×10−31kg
- R = 10−10m
Calculating χ:
χ=(4π×10−7)(1.6×10−19)2(9.1×10−31)(10−10)
Calculating the numerator:
=4π×10−7×2.56×10−38≈3.2×10−6
Calculating the denominator:
=9.1×10−31×10−10=9.1×10−41
Now substituting back:
χ≈3.2×10−69.1×10−41≈3.51×1034
Step 8: Compare with the value of χ for solid materials
The value of χ for solid materials is approximately 10−5. Thus:
3.51×103410−5≈3.51×1039
This shows that the calculated χ is significantly larger than typical values for solid materials.
Magnetic susceptibility (χ) is defined as the ratio of magnetization (M) to the magnetic field strength (H):
χ=MH
Both magnetization (M) and magnetic field strength (H) have the same dimensions, which makes χ a dimensionless quantity. Thus, the dimensions of χ are:
Dimensions of χ=(χ)=1(dimensionless)
We need to construct a quantity with the dimensions of χ using the parameters: e (charge), m (mass of electron), v (velocity of electron), R (Bohr radius), and μ₀ (permeability of free space).
- Mass (m): (m) = (M)
- Velocity (v): (v) = (L)(T)⁻¹
- Bohr radius (R): (R) = (L)
- Permeability of free space (μ₀): (μ₀) = (M)(L)⁰(T)⁻²(Q)²
We will express χ in terms of the parameters:
χ∼μ0e2mavbRc
where a, b, and c are constants we need to determine.
Substituting the dimensions into the equation gives:
Dimensions of χ=(μ0)(e2)(ma)(vb)(Rc)
This can be expressed as:
(M)(L)−2(T)0(Q)2⋅(M)a⋅(L)b(T)−b⋅(L)c
Combining these gives:
(M)1+a(L)−2+b+c(T)−b(Q)2
Since χ is dimensionless, we set the powers of M, L, T, and Q to zero:
1. 1+a=0
2. −2+b+c=0
3. −b=0
4. 2=0 (not applicable since we don't have charge in the final expression)
Now substituting a, b, and c back into the expression for χ:
χ∼μ0e2mR
Substituting the known values:
- μ₀ = 4π×10−7T m/A
- e = 1.6×10−19C
- m = 9.1×10−31kg
- R = 10−10m
χ=(4π×10−7)(1.6×10−19)2(9.1×10−31)(10−10)
=4π×10−7×2.56×10−38≈3.2×10−6
=9.1×10−31×10−10=9.1×10−41
χ≈3.2×10−69.1×10−41≈3.51×1034
The value of χ for solid materials is approximately 10−5. Thus:
3.51×103410−5≈3.51×1039
This shows that the calculated χ is significantly larger than typical values for solid materials.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Long Answer Type Question
10 Videos
- MOVING CHARNGES AND MAGNETISMBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MOVING CHARNGES AND MAGNETISMEXERCISE - Long Answer Type Questions
7 Videos
Similar Questions
The Betatron was the first important machine for producing high energy electrons. The action of the betatron depends on the same fundamental principle as that of the transformer in which an alternating current applied to a primary coil induces an altermating current usually with higher or lower voltage in the secondary coil. In the betatron secondary coil is replaced by a doughnut shaped vacuum chamber.Electron produced in the doughnut from a hot filament, are given a preliminary acceleration by the application of an electric field having potential difference of 20kV to 70kV, when an alternating magnetic field is applied parallel to the axis of the tube, two effects are produced (1) an electromotive force is produced in the electron orbit by the changing magnetic flux that gives an additional energy to the electrons (2) a radial force is produced by the action of magnetic field whose direction is perpendicular to the electron velocity. Which keeps the electron moving in a circular path. Conditions are arranged such that the increasing magnetic field keeps the electron in a circular orbit of constant radius. The mathematical relation between the betatron parameters to ensure the above condition is called BETATRON condition.
If the orbit radius of the circular path traced by the electron is R, magnetic field is B, speed of the electron is v, mass of the electron is m, charge on the electron is e and ϕ is the flux within the orbit of radius R. Then answer the following questions based on the above comprehension.
What is the value of d(m|→v|)dt ?
View SolutionIn an ordianary atom, as a first approximation, the motion of the nucleus can be ignored. In a positronium atom a positronreplaces the proton of hydrogen atom. The electron and positron masses are equal and , therefore , the motion of the positron cannot be ignored. One must consider the motion of both electron and positron about their center of mass. A detailed analyasis shows that formulae of Bohr's model apply to positronium atom provided that we replace me by what is known reduced mass is me/2.
If the Rydberg constant for hydrogen atom is R , then the Rydberg constant for positronium atom is
View SolutionThe wave function ψn,l,m is a mathematical function whose value depends upon spherical polar coordinates (r,θ,ϕ) of the electron and characterized by the quantum numbers n,l and m. Here r is distance from nucleus θ is colatitude and ϕ is azimuth. In the mathematical functions given in the Table, Z is atomic number and a0 is Bohr radius.

For the given orbital in Column 1 the only Correct combination for any hydrogen -like species is
View SolutionThe wave function, Ψn,l,ml is a mathematical function whose value depends upon spherical polar coordinates (r,θ,ϕ) of the electron and characterized by the quantum numbers n, l and nl, Here r is distance from nucleus, θ is colatitude and ϕ is azimuth. In the mathematical functions given in the Table, Z is atomic number and a0 is Bohr radius.

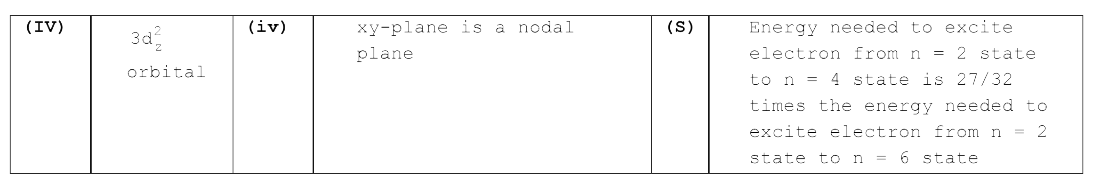
For the given orbital in Column 1, the only CORRECT combination for any hydrogen-like species is:
View SolutionHydrogen is the simplest atom of nature. There is one proton in its nucleus and an electron moves around the nucleus in a circular orbit. According to Niels Bohr's, this electron moves in a stationary orbit, if emits no electromagnetic radiation. The angular momentum of the electron is quantized , i.e., mvr=(nh/2π), where m= mass of the electron , v=velocity of the electron in the orbit , r=radius of the orbit , and n=1,2,3.... When transition takes place from Kth orbit to Jth orbit, energy photon is emitted. If the wavelength of the emitted photon is λ.
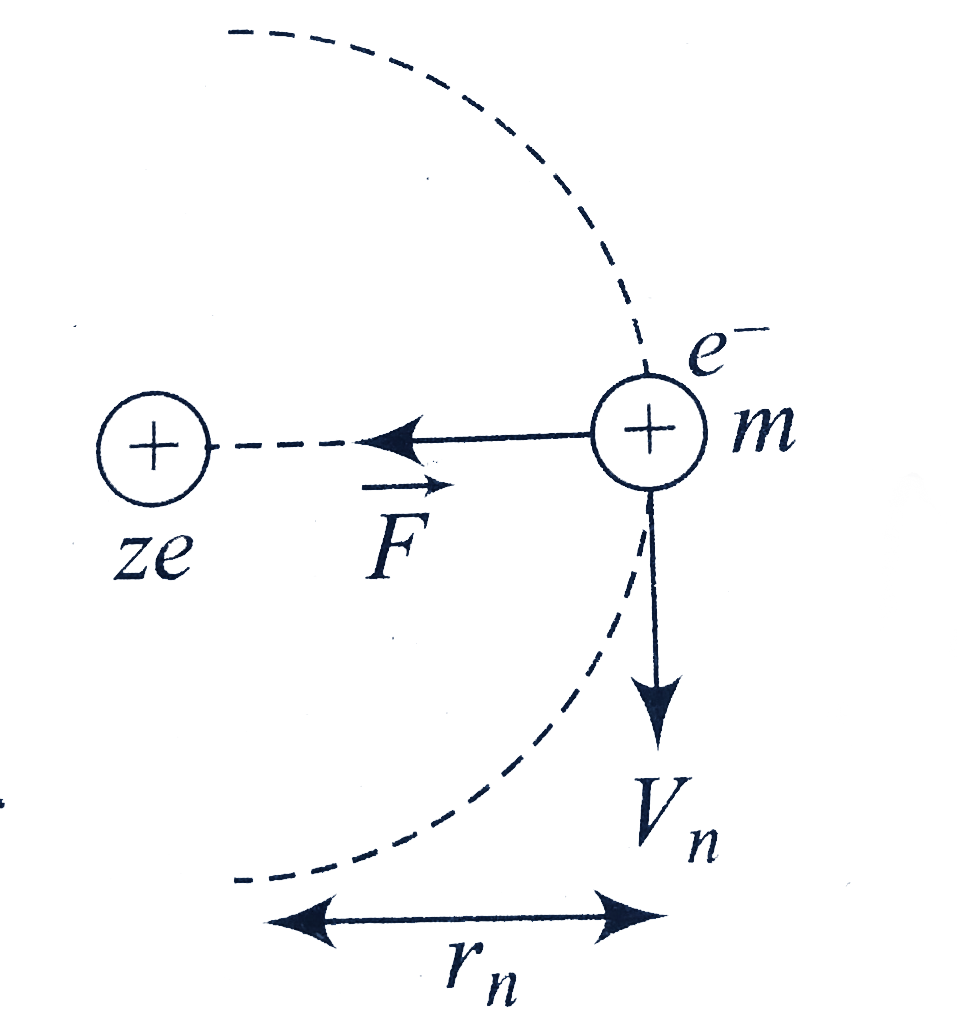
we find that 1λ=R[1J2−1K2], where R is
Rydberg's constant.
On a different planed, the hydrogen atom's structure was somewhat different from ours. The angular momentum of electron was P=2n(h/2π). i.e., an even multipal of (h/2π).
Answer the following questions regarding the other planet based on above passage:
In our world, the velocity of electron is v0 when the hydrogen atom is in the ground state on the other planet should be
View SolutionThe wave function, Ψn,l,ml is a mathematical function whose value depends upon spherical polar coordinates (r,θ,ϕ) of the electron and characterized by the quantum numbers n, l and nl, Here r is distance from nucleus, θ is colatitude and ϕ is azimuth. In the mathematical functions given in the Table, Z is atomic number and a0 is Bohr radius.
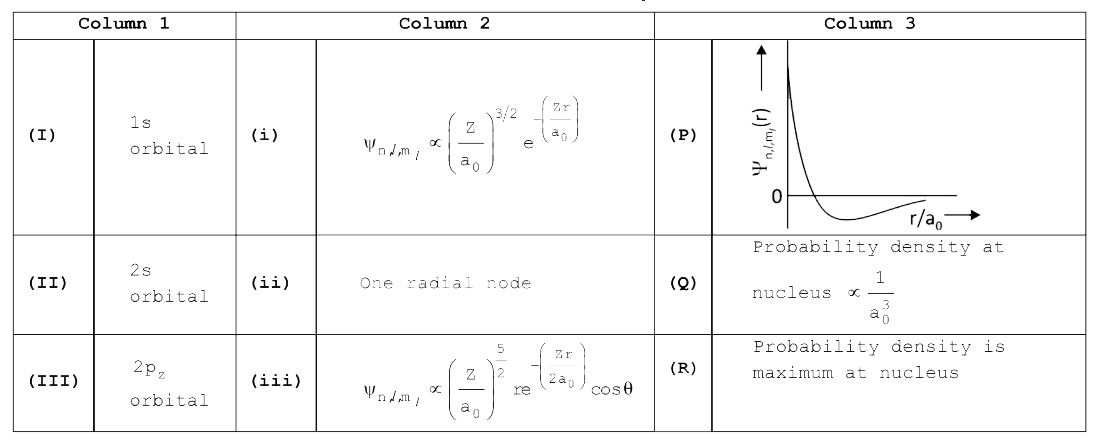
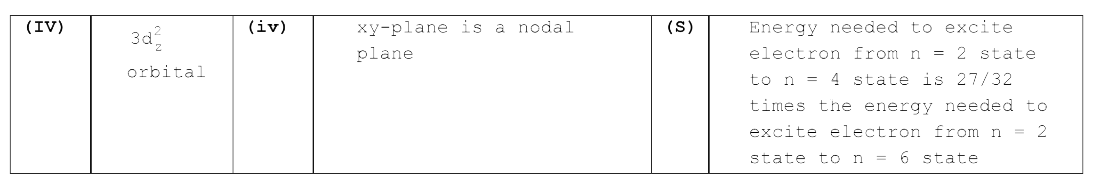
For ion, the only INCORRECT combination is:
View SolutionThe Betatron was the first important machine for producing high energy electrons. The action of the betatron depends on the same fundamental principle as that of the transformer in which an alternating current applied to a primary coil induces an altermating current usually with higher or lower voltage in the secondary coil. In the betatron secondary coil is replaced by a doughnut shaped vacuum chamber.Electron produced in the doughnut from a hot filament, are given a preliminary acceleration by the application of an electric field having potential difference of 20kV to 70kV, when an alternating magnetic field is applied parallel to the axis of the tube, two effects are produced (1) an electromotive force is produced in the electron orbit by the changing magnetic flux that gives an additional energy to the electrons (2) a radial force is produced by the action of magnetic field whose direction is perpendicular to the electron velocity. Which keeps the electron moving in a circular path. Conditions are arranged such that the increasing magnetic field keeps the electron in a circular orbit of constant radius. The mathematical relation between the betatron parameters to ensure the above condition is called BETATRON condition.
If the orbit radius of the circular path traced by the electron is R, magnetic field is B, speed of the electron is v, mass of the electron is m, charge on the electron is e and ϕ is the flux within the orbit of radius R. Then answer the following questions based on the above comprehension.
What is the tangential force acting on the electron ?
View SolutionThe Betatron was the first important machine for producing high energy electrons. The action of the betatron depends on the same fundamental principle as that of the transformer in which an alternating current applied to a primary coil induces an altermating current usually with higher or lower voltage in the secondary coil. In the betatron secondary coil is replaced by a doughnut shaped vacuum chamber.Electron produced in the doughnut from a hot filament, are given a preliminary acceleration by the application of an electric field having potential difference of 20kV to 70kV, when an alternating magnetic field is applied parallel to the axis of the tube, two effects are produced (1) an electromotive force is produced in the electron orbit by the changing magnetic flux that gives an additional energy to the electrons (2) a radial force is produced by the action of magnetic field whose direction is perpendicular to the electron velocity. Which keeps the electron moving in a circular path. Conditions are arranged such that the increasing magnetic field keeps the electron in a circular orbit of constant radius. The mathematical relation between the betatron parameters to ensure the above condition is called BETATRON condition.
If the orbit radius of the circular path traced by the electron is R, magnetic field is B, speed of the electron is v, mass of the electron is m, charge on the electron is e and ϕ is the flux within the orbit of radius R. Then answer the following questions based on the above comprehension.
What is the BETATRON condition ?
View SolutionHydrogen is the simplest atom of nature. There is one proton in its nucleus and an electron moves around the nucleus in a circular orbit. According to Niels Bohr's, this electron moves in a stationary orbit, if emits no electromagnetic radiation. The angular momentum of the electron is quantized , i.e., mvr=(nh/2π), where m= mass of the electron , v=velocity of the electron in the orbit , r=radius of the orbit , and n=1,2,3.... When transition takes place from Kth orbit to Jth orbit, energy photon is emitted. If the wavelength of the emitted photon is λ.
we find that 1λ=R[1J2−1K2], where R is
Rydberg's constant.
On a different planet, the hydrogen atom's structure was somewhat different from ours. The angular momentum of electron was P=2n(h/2π). i.e., an even multiple of (h/2π).
Answer the following questions regarding the other planet based on above passage:
In our world, the ionization potential energy of a hydrogen atom is 13.6eV. On the other planet, this ionization potential energy will be
View SolutionDirection :
Resistive force proportional to object velocity
At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as
R=−bv
Where v is the velocity of the object and b is a positive constant that depends onthe properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity.
Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here.
Thus mg−bv=mdvdt⇒dvdt=g−bmv
Solving the equation
v=mgb(1−e−bt/m)
where e=2.71 is the base of the natural logarithm
The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v1 and then on it continues to move with zero acceleration
mg−bT=0
⇒mT=mgb
Hence v=vT(1−evtm)
In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table.
ObjectIIIIIIVMass (in kg.)1234Constant bin (N-s)/m3.71.41.42.8
If an object of mass 2 kg and constant b=4N−sm has terminal speed vT in a liquid then time required to reach 0.63vT from start of the motion is :
View Solution
