There are two current carrying planar coils made each from identical wires of length L. C1 is the circular (radius R) and C2 is square (side a). They are so constructed that they have same frequency of oscillation when they are placed in the same uniform →B and carry the same current i. Find a in terms of R.
To solve the problem, we need to find the side length a of the square coil C2 in terms of the radius R of the circular coil C1. Both coils are made from identical wires of length L and carry the same current I while oscillating in the same uniform magnetic field →B.
1. Determine the number of turns for the square coil C2:
The perimeter of the square coil is 4a. Since the total length of the wire is L, the number of turns N1 in the square coil is given by:
N1=L4a
2. Calculate the magnetic moment m1 of the square coil:
The area A1 of the square coil is a2. The magnetic moment m1 is given by:
m1=N1⋅I⋅A1=(L4a)⋅I⋅a2=LIa4
3. Determine the number of turns for the circular coil C1:
The circumference of the circular coil is 2πR. The number of turns N2 in the circular coil is given by:
N2=L2πR
4. Calculate the magnetic moment m2 of the circular coil:
The area A2 of the circular coil is πR2. The magnetic moment m2 is given by:
m2=N2⋅I⋅A2=(L2πR)⋅I⋅πR2=LIR2
5. Relate the time periods of oscillation for both coils:
The time period T of oscillation for a coil in a magnetic field is given by:
T=2π√ImB
where I is the moment of inertia, m is the magnetic moment, and B is the magnetic field.
For the square coil:
T1=2π√I1m1B
For the circular coil:
T2=2π√I2m2B
Since both coils have the same frequency of oscillation, we have T1=T2.
6. Equate the time periods:
√I1m1=√I2m2
Squaring both sides gives:
I1m1=I2m2
7. Calculate the moments of inertia I1 and I2:
- For the square coil:
I1=Ma212
- For the circular coil:
I2=MR22
8. Substituting the values into the equation:
Ma212LIa4=MR22LIR2
Simplifying gives:
a23=R
9. Solve for a:
a2=3R⟹a=√3R
Thus, the side length a of the square coil in terms of the radius R of the circular coil is:
a=√3R
The perimeter of the square coil is 4a. Since the total length of the wire is L, the number of turns N1 in the square coil is given by:
N1=L4a
The area A1 of the square coil is a2. The magnetic moment m1 is given by:
m1=N1⋅I⋅A1=(L4a)⋅I⋅a2=LIa4
The circumference of the circular coil is 2πR. The number of turns N2 in the circular coil is given by:
N2=L2πR
The area A2 of the circular coil is πR2. The magnetic moment m2 is given by:
m2=N2⋅I⋅A2=(L2πR)⋅I⋅πR2=LIR2
The time period T of oscillation for a coil in a magnetic field is given by:
T=2π√ImB
where I is the moment of inertia, m is the magnetic moment, and B is the magnetic field.
T1=2π√I1m1B
For the circular coil:
T2=2π√I2m2B
√I1m1=√I2m2
Squaring both sides gives:
I1m1=I2m2
- For the square coil:
I1=Ma212
- For the circular coil:
I2=MR22
Ma212LIa4=MR22LIR2
Simplifying gives:
a23=R
a2=3R⟹a=√3R
a=√3R
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Long Answer Type Question10videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MOVING CHARNGES AND MAGNETISMEXERCISE - Long Answer Type Questions7videos
MOVING CHARNGES AND MAGNETISM
Similar Questions
Two wires of same length are shaped into a square and a circle. If they carry same current, ratio of the magnetic moment is
View SolutionTwo wires of the same length are shaped into a square and a circle. If they carry same current, ratio of the magnetic moment is
View SolutionA semi circular arc of radius r and a straight wire along the diameter, both are carrying same current i find out magnetic force per unit length on the small element P, which is at the centre of curvature.
 View Solution
View SolutionShow that the force on a wire between a and b of arbitrary of figure is the same as force on the straigth wire between the same two points when they carry the same current from a to b and are plassed in the same magnetic field. Also find the force.
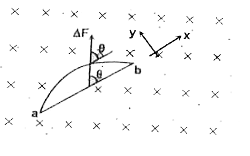 View Solution
View SolutionA length of wire carries a steady current. It is first bent to form a circular coil of one turn. The same length is now bent more sharply to give a loop of two turns of smaller radius. The magentic field at the centre caused by the same current now will be
View SolutionTwo identical circular wires P and Q each of radius R and carrying current 'I' are kept in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net magnetic field at the common centre of the two coils.
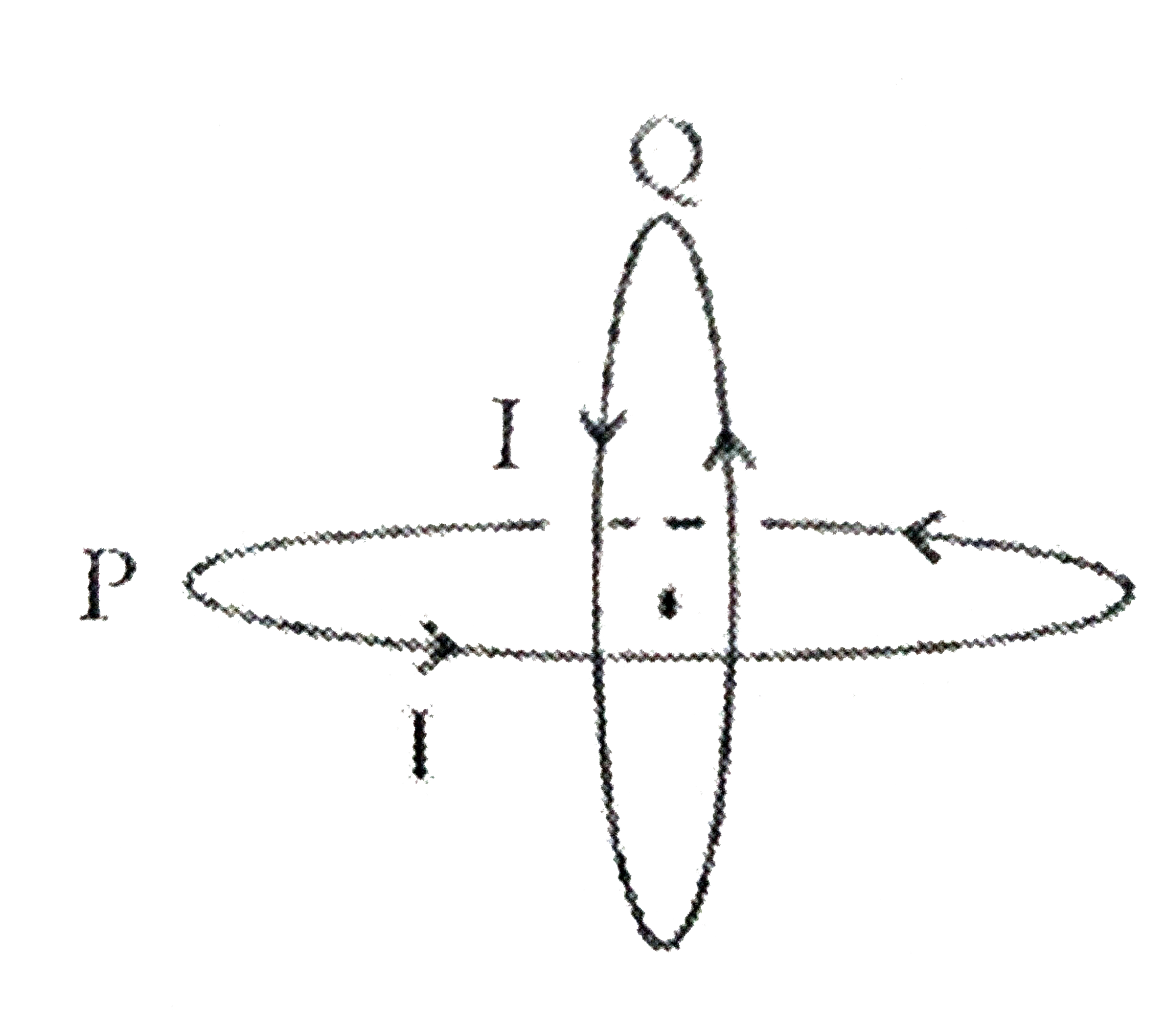 View Solution
View SolutionA circular coil of radius 2R is carrying current 'i' . The ratio of magnetic fields at the centre of the coil and at a point at a distance 6R from the centre of the coil on the axis of the coil is
View SolutionA thin circular wire carrying a current I has a magnetic moment M. The shape of the wire is changed to a square and it carries the same current. It will have a magnetic moment
View SolutionA steady current is flowing in a circular coil of radius R, made up of a thin conducting wire. The magnetic field at the centre of the loop is BL. Now, a circular loop of radius R/n is made from the same wire without changing its length, by unfounding and refolding the loop, and the same current is passed through it. If new magnetic field at the centre of the coil is BC, then the ratio BL/BC is
View SolutionA steady current is flowing in a circular coil of radius R, made up of a thin conducting wire. The magnetic field at the centre of the loop is BL. Now, a circular loop of radius R/n is made from the same wire without changing its length, by unfounding and refolding the loop, and the same current is passed through it. If new magnetic field at the centre of the coil is BC, then the ratio BL/BC is
View Solution

