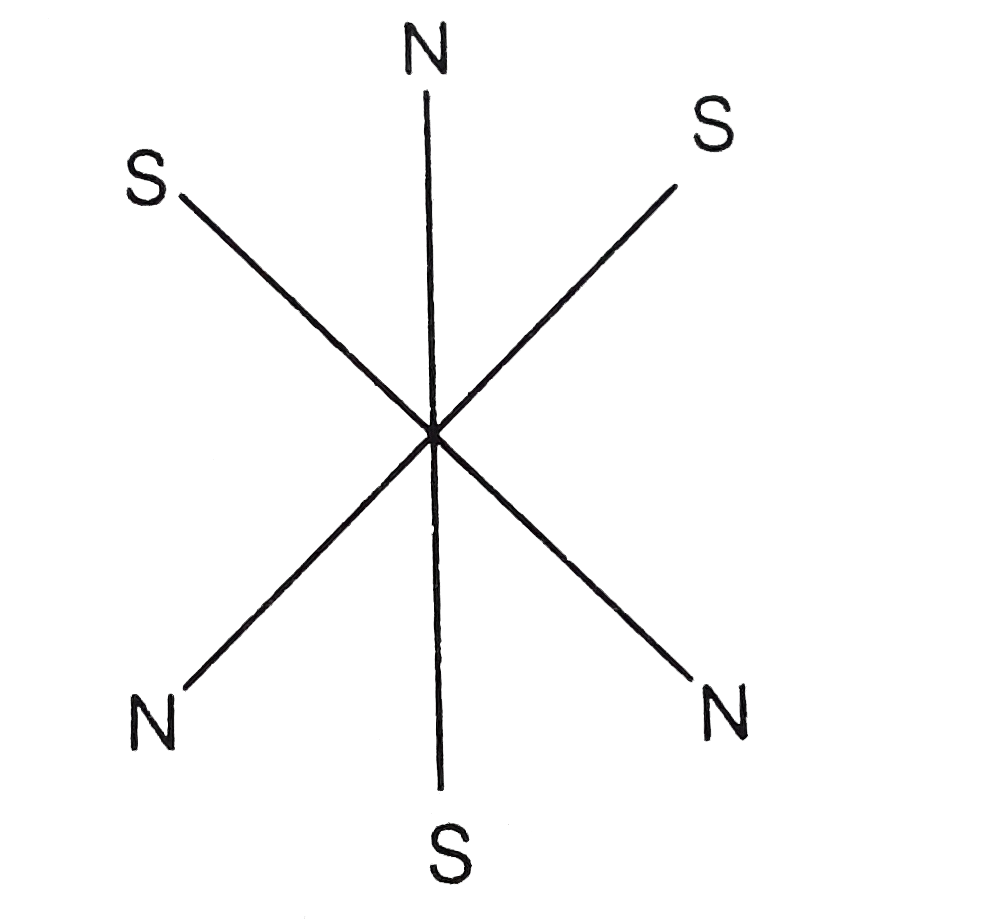
Three identical bar magnets are rivetted together at centre in the same place as shown in figure. This system is placed at rest in a slowly varying magnetic field. It is found that the system of magnets does not show any motion. The north-south poles of one magnet are shown in figure. Determine the poles of the remaining two.

The system will be in stable equilibrium if the net force on the system is zero and net torque on the system is also zero. This is possible only when the poles of the remaining two magnets are as given in the figure.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Long Answer Type Question
10 Videos
- MOVING CHARNGES AND MAGNETISMBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MOVING CHARNGES AND MAGNETISMEXERCISE - Long Answer Type Questions
7 Videos
Similar Questions
Knowledge Check
Two identical bar magnets are fixed with their centres at a distance d apart. A stationary charge Q is placed at P in between the gap of the two magnets at distance D from the centre O as shown in the figure. The force on the charge Q is
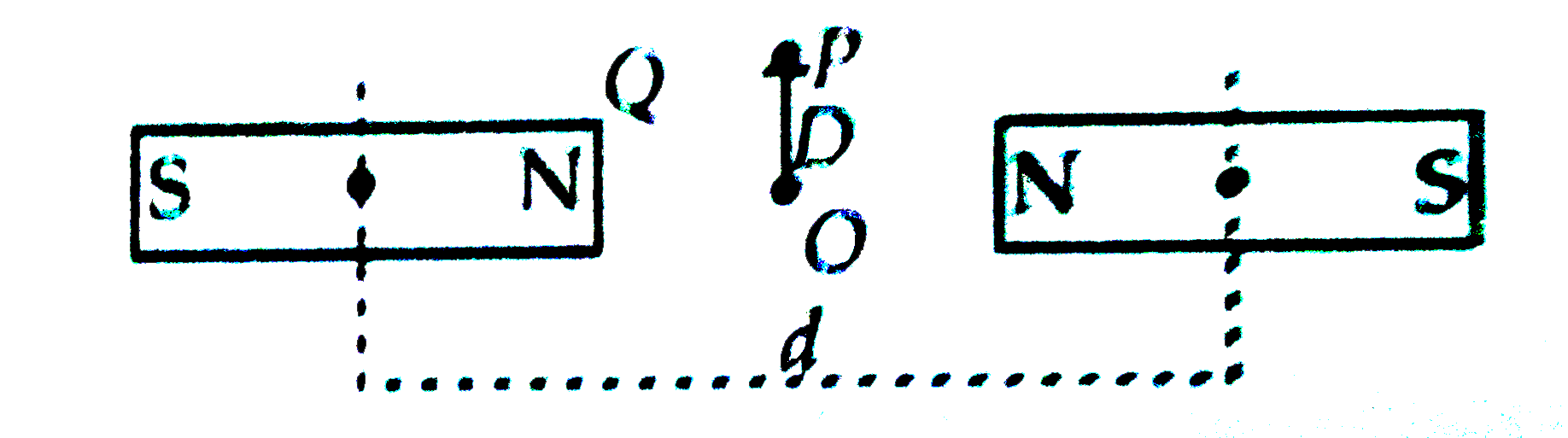 AzeroBdirected along OPCdirected along PODdirected perpendicular to the plane of paper
AzeroBdirected along OPCdirected along PODdirected perpendicular to the plane of paper
Magnetic field strength at the centre of regular pentagon made of a conducting wire of uniform cross section area as shown in figure is:

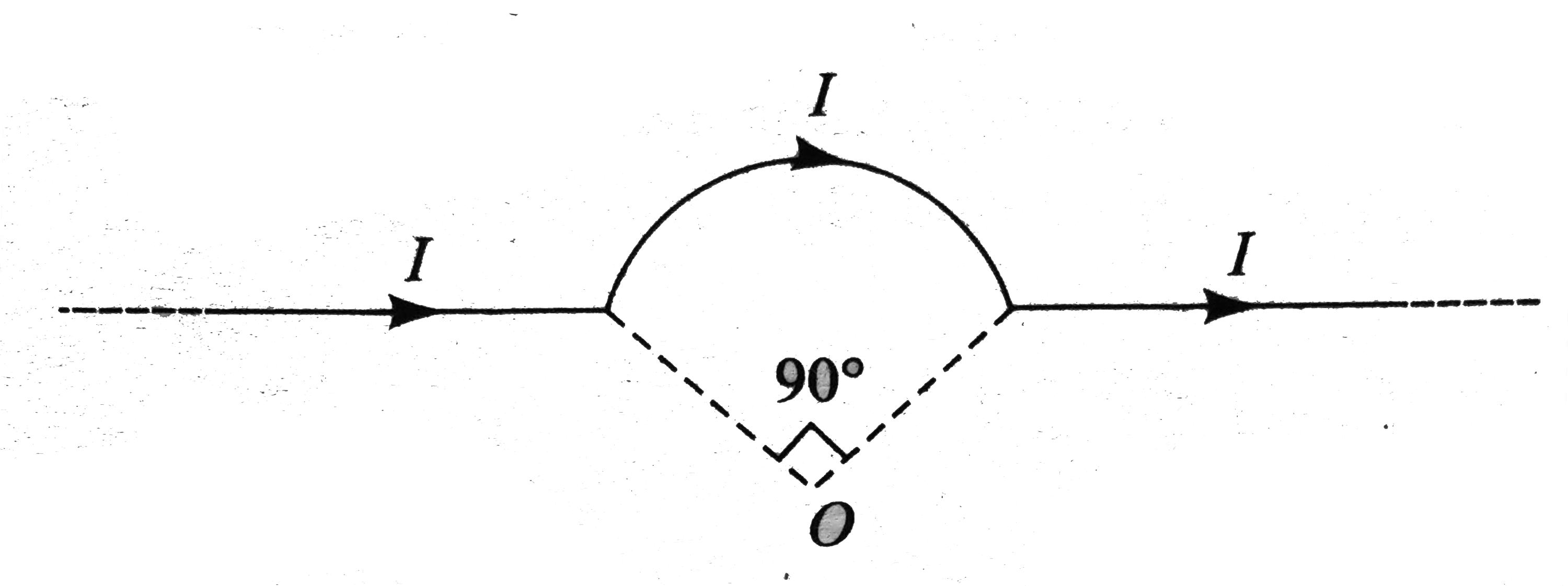
View SolutionFind the magnetic field at the centre of the circular loop shown in figure.

View SolutionFind the magnetic field at the centre O of the loop shown in the figure
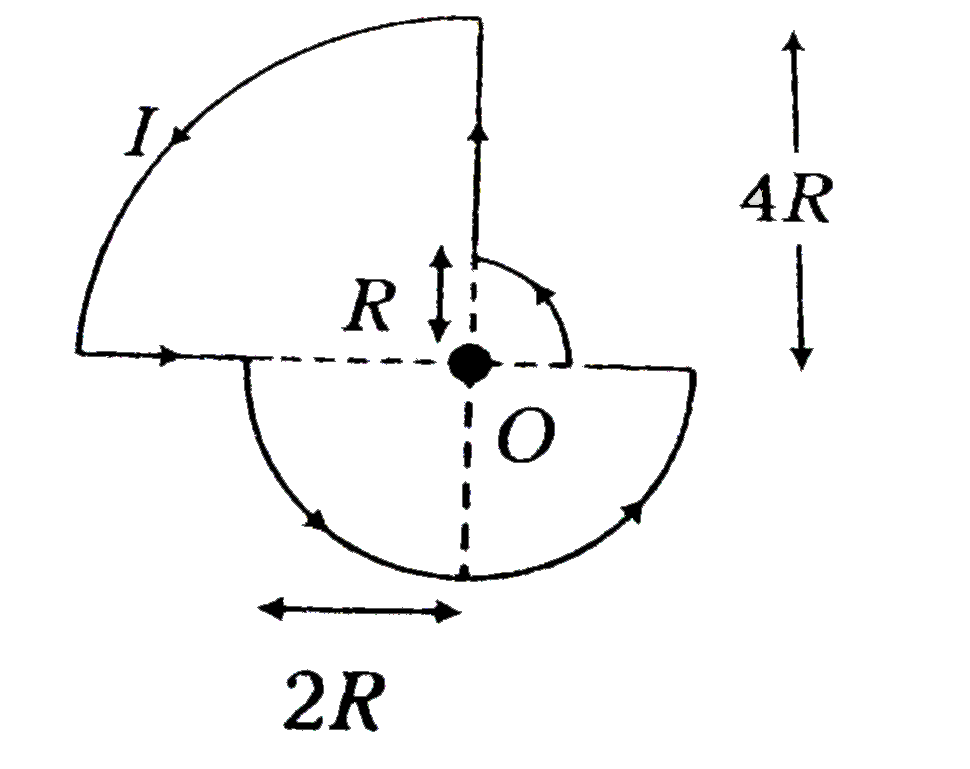
View SolutionFind the magnetic field at the centre O of the loop shown in the figure
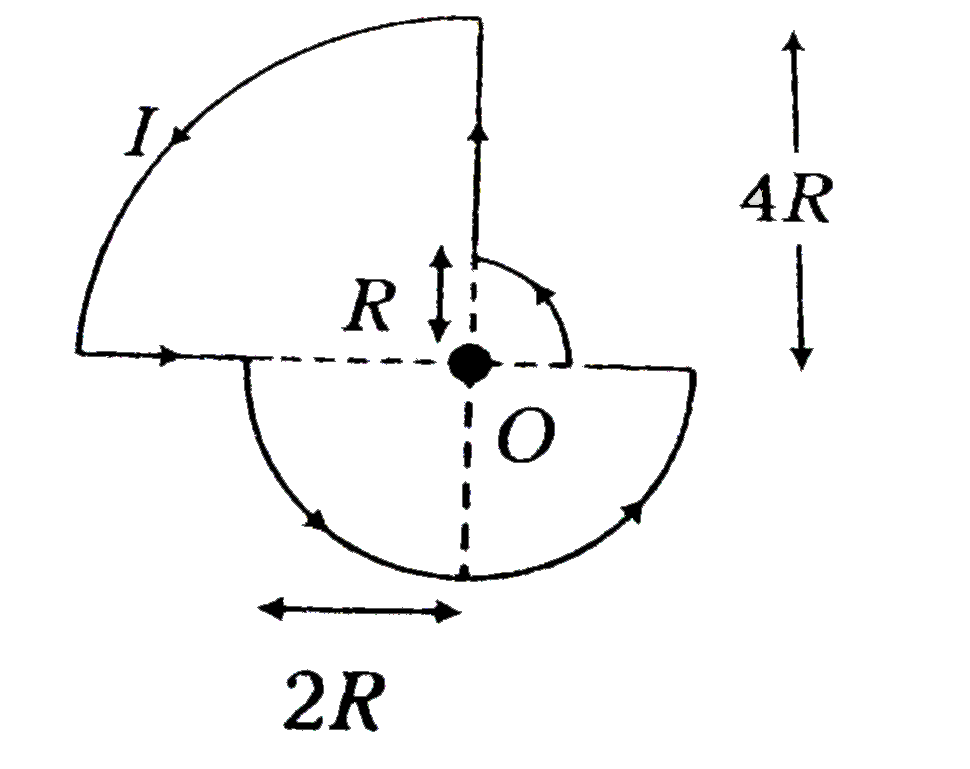
View SolutionB0 is the magnetic field at point P for a given straight wire as shown in figure. If this wirre is bent into a circular loop, then magnetic field at the centre of loop is
_PHY_E06_130_Q01.png)
View SolutionA bar magnet of magnetic moment M is cut into four identical parts as shown in figure, then magnetic moment of each part is
_PHY_E06_282_Q01.png)
View SolutionTwo magnets of equal magnetic moments M each are placed as shown in figure below . The resultant magnetic moment is M . Then value of θ is

View Solution