Use i the Ampere's law for H and ii continuity of lines of B, to conclude that inside a bar magnet, (a) lines of H run from the N-pole to S-pole while (b) lies of B must run from the S-pole to N -pole.
To solve the question regarding the behavior of magnetic fields inside a bar magnet using Ampere's law and the continuity of magnetic field lines, we can follow these steps:
1. Understanding Ampere's Law for H:
Ampere's law states that the line integral of the magnetic field intensity H around a closed loop is equal to the current enclosed by that loop. Mathematically, it can be expressed as:
∮H⋅dl=Ienc
Inside a bar magnet, there are no free currents, so Ienc=0.
2. Applying Ampere's Law:
For a closed loop inside the bar magnet, since there are no free currents, we have:
∮H⋅dl=0
This implies that the contributions to the integral from opposite sides of the loop must cancel each other out.
3. Analyzing the Direction of H:
If we consider a path from point P (near the North pole) to point Q (near the South pole), the line integral ∮H⋅dl suggests that the direction of H must be from the North pole to the South pole inside the magnet. Therefore, we conclude:
Lines of H run from the North pole to the South pole.
4. Understanding the Continuity of B:
The magnetic field B is related to H by the equation:
B=μH
where μ is the permeability of the material. The lines of B must be continuous and form closed loops.
5. Analyzing the Direction of B:
Outside the bar magnet, B lines run from the North pole to the South pole. However, inside the magnet, the continuity of the magnetic field lines means that they must return from the South pole to the North pole. Thus, we conclude:
Lines of B run from the South pole to the North pole inside the bar magnet.
Final Conclusions:
- Inside a bar magnet, lines of H run from the North pole to the South pole.
- Inside a bar magnet, lines of B run from the South pole to the North pole.
Ampere's law states that the line integral of the magnetic field intensity H around a closed loop is equal to the current enclosed by that loop. Mathematically, it can be expressed as:
∮H⋅dl=Ienc
Inside a bar magnet, there are no free currents, so Ienc=0.
For a closed loop inside the bar magnet, since there are no free currents, we have:
∮H⋅dl=0
This implies that the contributions to the integral from opposite sides of the loop must cancel each other out.
If we consider a path from point P (near the North pole) to point Q (near the South pole), the line integral ∮H⋅dl suggests that the direction of H must be from the North pole to the South pole inside the magnet. Therefore, we conclude:
Lines of H run from the North pole to the South pole.
The magnetic field B is related to H by the equation:
B=μH
where μ is the permeability of the material. The lines of B must be continuous and form closed loops.
Outside the bar magnet, B lines run from the North pole to the South pole. However, inside the magnet, the continuity of the magnetic field lines means that they must return from the South pole to the North pole. Thus, we conclude:
Lines of B run from the South pole to the North pole inside the bar magnet.
- Inside a bar magnet, lines of H run from the North pole to the South pole.
- Inside a bar magnet, lines of B run from the South pole to the North pole.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Long Answer Type Question10videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MOVING CHARNGES AND MAGNETISMEXERCISE - Long Answer Type Questions7videos
MOVING CHARNGES AND MAGNETISM
Similar Questions
When the N-pole of a bar magnet points towards the south and S-pole towards the north, the null points are at the
View SolutionA circular loop placed in a plane perpendicular to the plane of paper carries a current when the key in ON, [figure]. The current as seen from pionts A and B (in the plane of paper and on the axis of the coil) is anticlockwise and clockwise respectively. The magnetic field lines point from B to A. The N-pole of the resultant magnet is on the face close to:
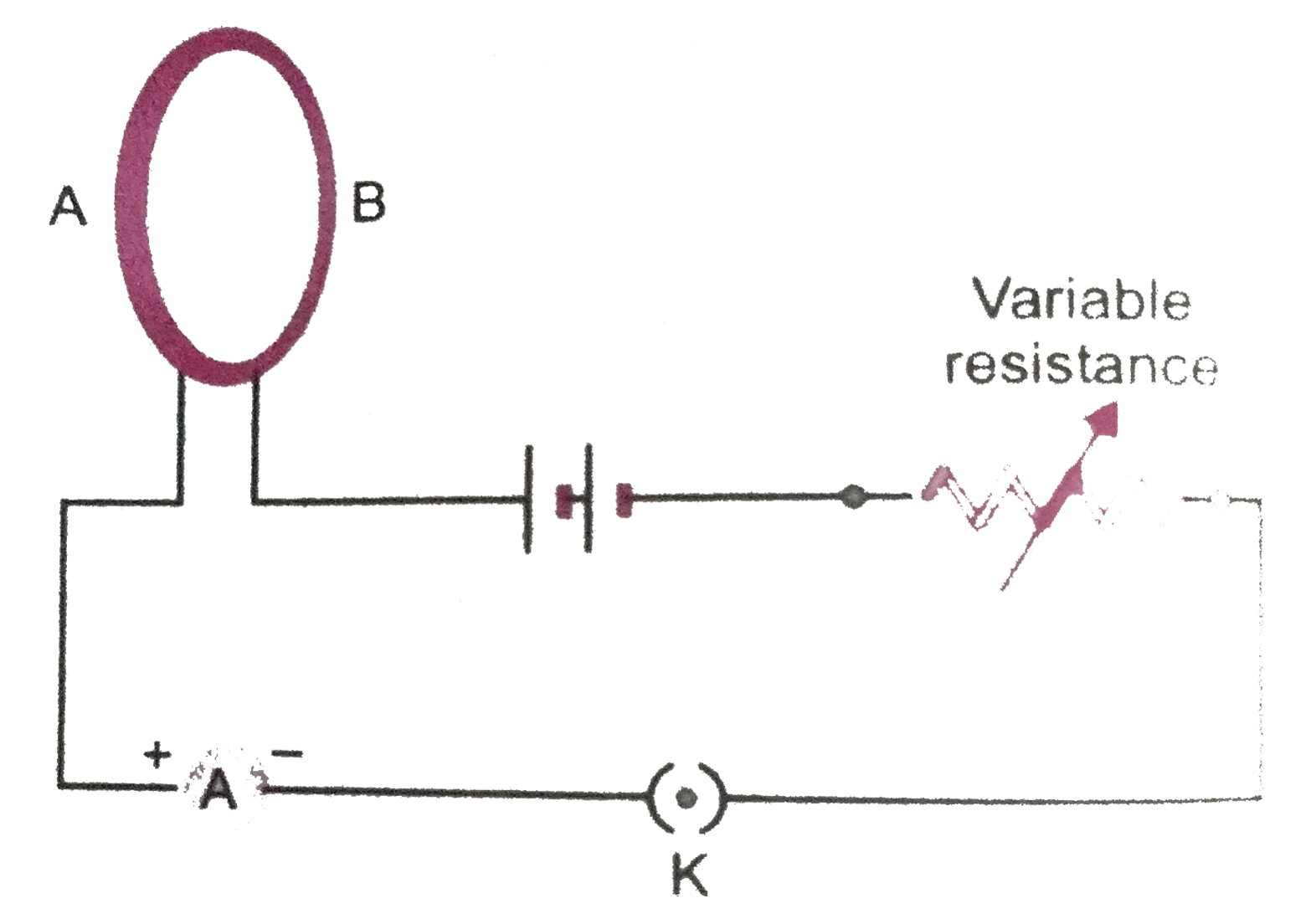 View Solution
View SolutionWith reference to the given figure, a man stands on the ground at point A, Which is on the same horizontal plane as B, the foot of the vertical pole BC. The height of the pole is 10 m . The man's eye is 2 m above the ground. He observes the angle of elevation of C, the top of the pole, as x∘ , where tan x∘=25 . Calculate :
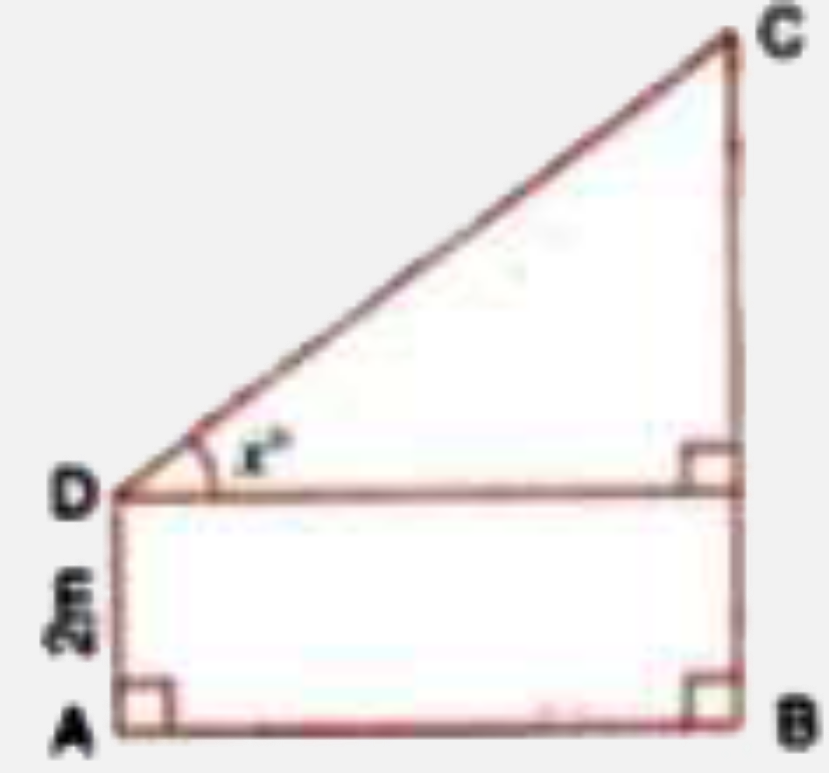
angle of elevation of the top of the pole when he is standing 15 metres from the pole. Give your answer to the nearest degree.View SolutionAB is a vertical pole with B at the ground level and and A at the top .A man finds that the angle of elevation of the point A from a certain point C on the ground is 60∘ . He moves away from the pole along the line BC to a point D such that CD = 7 m .From D . the angle of elevation of the point A is 45∘ .Find the height of the pole .
View Solution(a) What happens if a bar magnet is cut into two pieces (i) transverse to its length (ii) along its length?
(b) What happens if an iron bar magnet is melted? Does it retain its magnetism?
(c) A magnetised needle in a uniform magnetic field experiences a torque but no net force. However, an iron nail near a bar magnet experiences a force of attration in addition to a torque, explain.
(d) Must every magnetic field configuration have a north pole and a south pole? What about the field due to a toroid?
(e) Can you think of magnetic field configuration with three poles?
(f) Two identical looking iron bars A and B are given, one of which is definitely known to be magnetised. How would one ascertain whether or not both are magnetised? If only one is magnetised how does one ascertain which one? Use nothing else but the bars A and B.View SolutionA short linear object of length b lies along the axis of a concave mirror or focal length f at a distance u from the pole of the mirror. The size of the image is approximately equal to
View SolutionAB is a vertical pole with B at the ground level and A at the top. A man finds that the angle of elevation of the point A from a certain point C on the ground is 60o . He moves away from the pole along the line BC to a point D such that CD=7m . From D the angle of elevation of the point A is 45o . Then the height of the pole is (1) 7√321√3−1m (2) 7√32√3+1m (3) 7√32√3−1m (4) 7√32√3+1m
View SolutionFrom a point on the ground at a distance a from the foot of a pole, a ball is thrown at an angle of 45∘, which just touches the top of the pole and strikes the ground at a distance of b, on the outer side of it. Find the height of the pole.
View SolutionOn a horizontal flat ground, a person is standing at a point A. At this point, he installs a 5m long pole vertically. Now , he moves 5m towards east and then 2m towards north and reaches at a point B. There he installs another 3m long vertical pole . A bird flies from the top of the first pole to the top of the swecond pole. Find the displacement and magnitude of the displacement of the bird.
View SolutionA pole has to be erected at a point on the boundary of a circular park of diameter 13 metres in such a way that the difference of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. Is it the possible to do so? If yes, at what distances from the two gates should the pole be erected?
View Solution

