Two pendulum bobs of masses m and 2m collide head on elastically at the lowest point in their motion. If both the balls are released from a height H above the lowest point, to what heights do they rise for the first time after collision?
The correct Answer is:B
To solve the problem of two pendulum bobs of masses m and 2m colliding elastically at the lowest point in their motion, we will follow these steps:
Step 1: Calculate the initial velocities of the pendulum bobs just before the collision.
Using the conservation of energy, we can find the velocities of both bobs just before the collision.
For the first bob (mass m):
- It is released from height H.
- The potential energy at height H converts to kinetic energy at the lowest point.
PE=KE⟹mgh=12mv21
Solving for v1:
v21=2gH⟹v1=√2gH
For the second bob (mass 2m):
- It is also released from height H.
PE=KE⟹2mgH=12(2m)v22
Solving for v2:
v22=2gH⟹v2=√2gH
Step 2: Apply conservation of momentum and kinetic energy for the elastic collision.
Let u1 and u2 be the velocities of the bobs after the collision.
Using the conservation of momentum:
mv1+2mv2=mu1+2mu2
Substituting v1 and v2:
m√2gH+2m√2gH=mu1+2mu2
Simplifying:
3m√2gH=mu1+2mu2
Dividing through by m:
3√2gH=u1+2u2(1)
Using conservation of kinetic energy:
12mv21+12(2m)v22=12mu21+12(2m)u22
Substituting the values:
12m(2gH)+12(2m)(2gH)=12mu21+12(2m)u22
Simplifying:
mgH+2mgH=12mu21+mgu22
3mgH=12mu21+mgu22
Dividing through by m:
3gH=12u21+gu22(2)
Step 3: Solve the equations (1) and (2).
From equation (1):
u1=3√2gH−2u2
Substituting u1 into equation (2):
3gH=12(3√2gH−2u2)2+gu22
This will yield a quadratic equation in terms of u2. Solving this will give us the values of u1 and u2.
Step 4: Calculate the heights after the collision.
Using the conservation of energy again for both bobs after the collision:
For bob m:
12mu21=mgh1⟹h1=u212g
For bob 2m:
12(2m)u22=(2m)gh2⟹h2=u222g
Final Heights:
After calculating u1 and u2 from the previous steps, we can find h1 and h2.
- It is released from height H.
- The potential energy at height H converts to kinetic energy at the lowest point.
- It is also released from height H.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Type 1
1 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Solved Examples
13 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
Two balls of masses m and 2m moving in opposite directions collide head on elastically with velocities v and 2v. Find their velocities after collision.
View SolutionTwo balls of masses m and 2m moving in opposite directions collide head on elastically with velocities v and 2v. Find their velocities after collision.
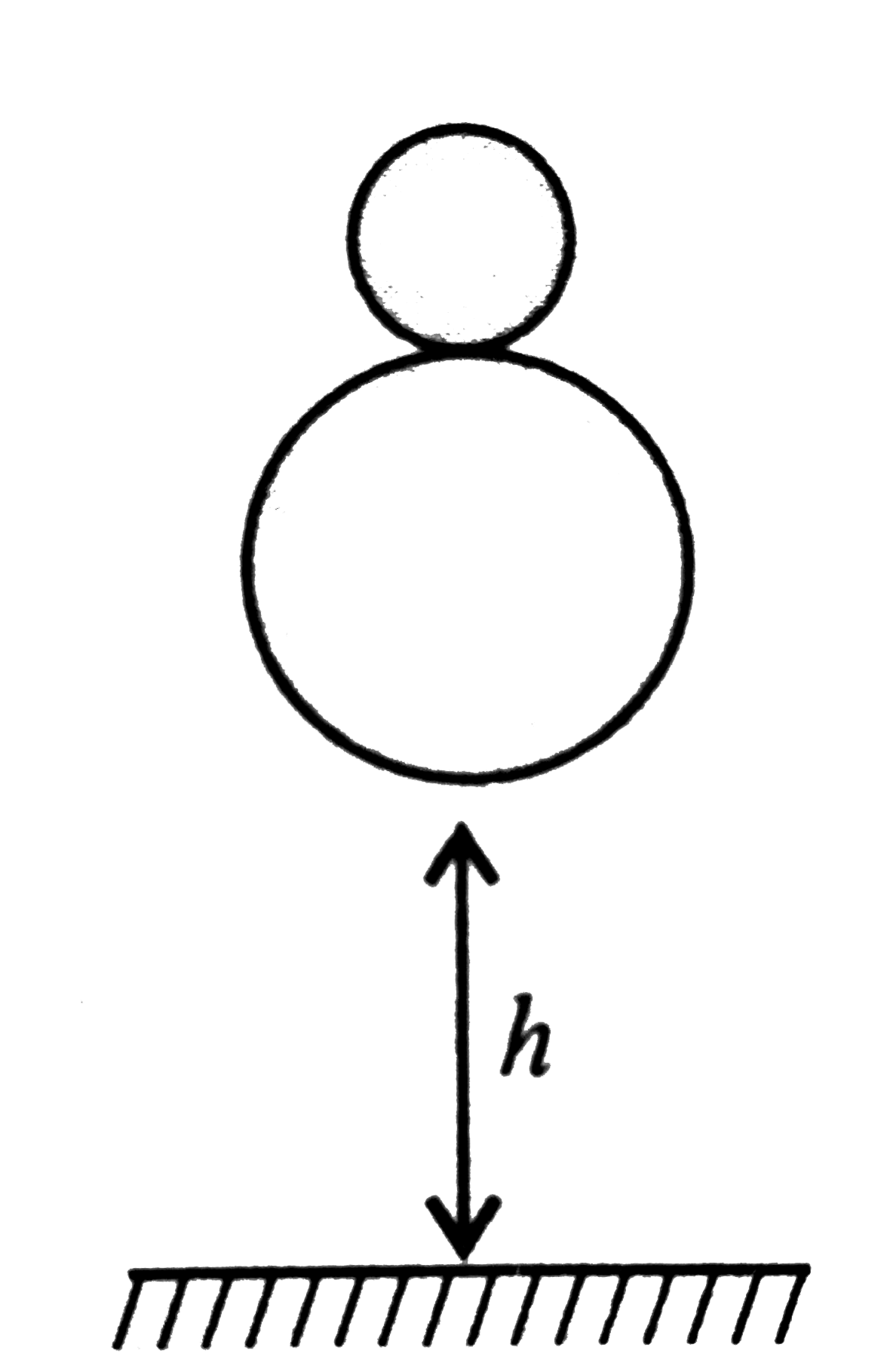
View SolutionA tennis ball with (small) mass m2 rests on the top of a basketball of mass m1which is at a height h above the ground, and the bottom of the tennis ball is at height h+d above the ground. The balls are dropped. To what height does the tennis ball bounce with respect to ground? (Assume all collisions to be elastic and m1>>m2)
View SolutionA hollow sphere of mass M lies on a rough horizontal plane when a particle of mass m traveling with speed v collides and sticks with it. If line of motion of the particle is at height h above the center of sphere, find h if the body rolls without slipping after collision (m<<M).
View SolutionA ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
View SolutionA simple pendulum of length l and mass m is initially at its lowest position. It is given the minimum horizontal speed necessary after to move in a circular path about the point of suspension. The tension in the string at the lowest positive of the bob is
View SolutionA small ball of mass m is connected by an inextensible massless string of length with an another ball of mass M=4m. They are released with zero tension in the string from a height h as shown in the figure. Find the time when the string becomes taut for the first time after the mass M collides with the ground. Take all collisions to be elastic.

View SolutionA smooth ball of mass 1kg is projected with velocity 7m/s horizontal from a tower of height 3.5m. It collides elastically with a wedge of mass 3 kg and inclination of 45∘ kept on ground. The ball collides with the wedge at a height of 1m above the ground. Find the velocity of the wedge and the ball after collision. (Neglect friction at any contact.)

View SolutionTwo massless string of length 5 m hang from the ceiling very near to each other as shown in the figure. Two balls A and B of masses 0.25kg and 0.5kg are attached to the string. The ball A is released from rest at a height 0.45m as shown in the figure. The collision between two balls is completely elastic. Immediately after the collision, the kinetic energy of ball B is 1J The velocity of ball A just after the collision is
Q01.png)
View SolutionA small ball of mass m moving with speed v collides elastically with a simple pendulum with bob of mass m at rest. The maximum height attained by the bob after collision is
View Solution
