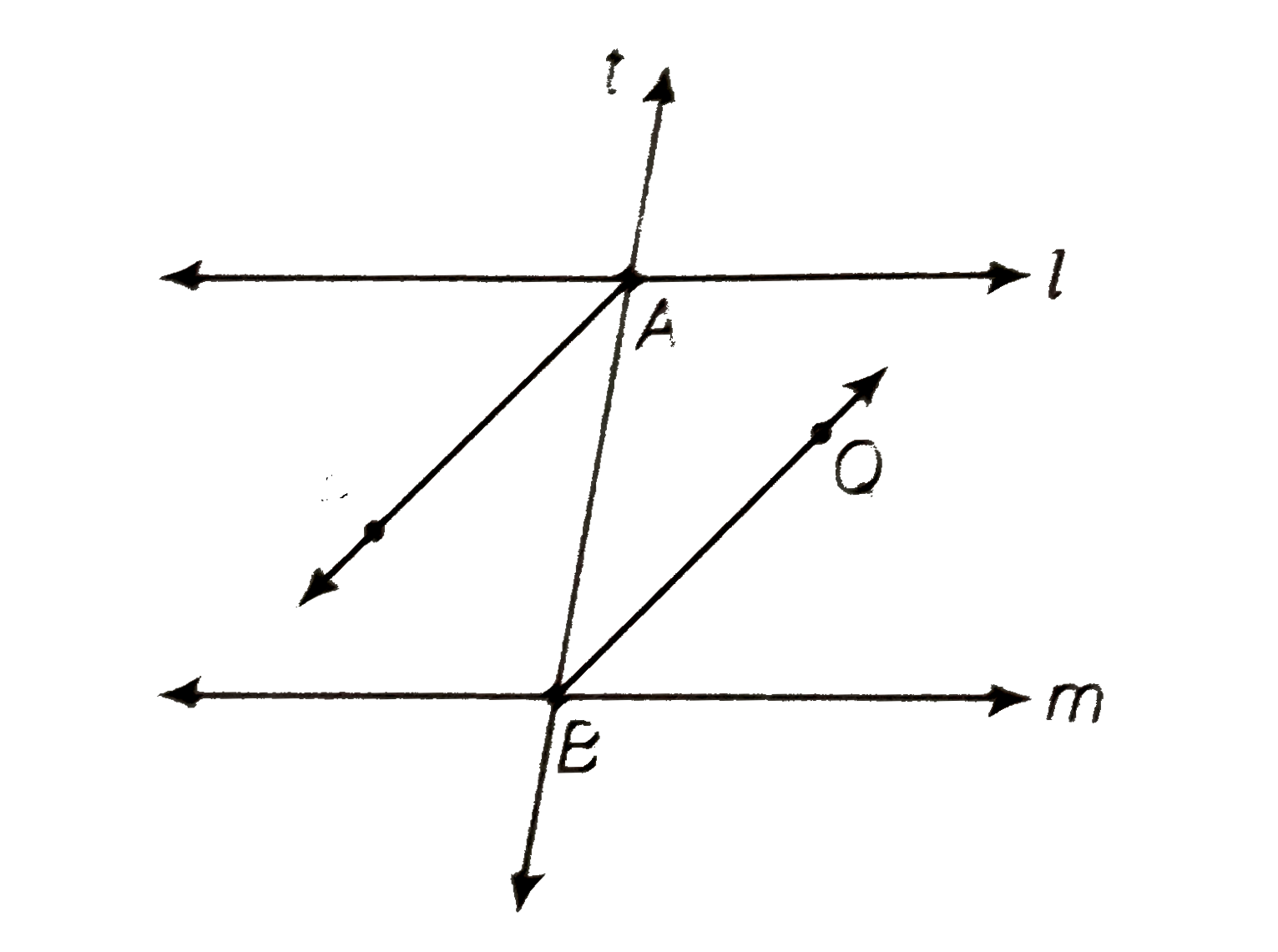
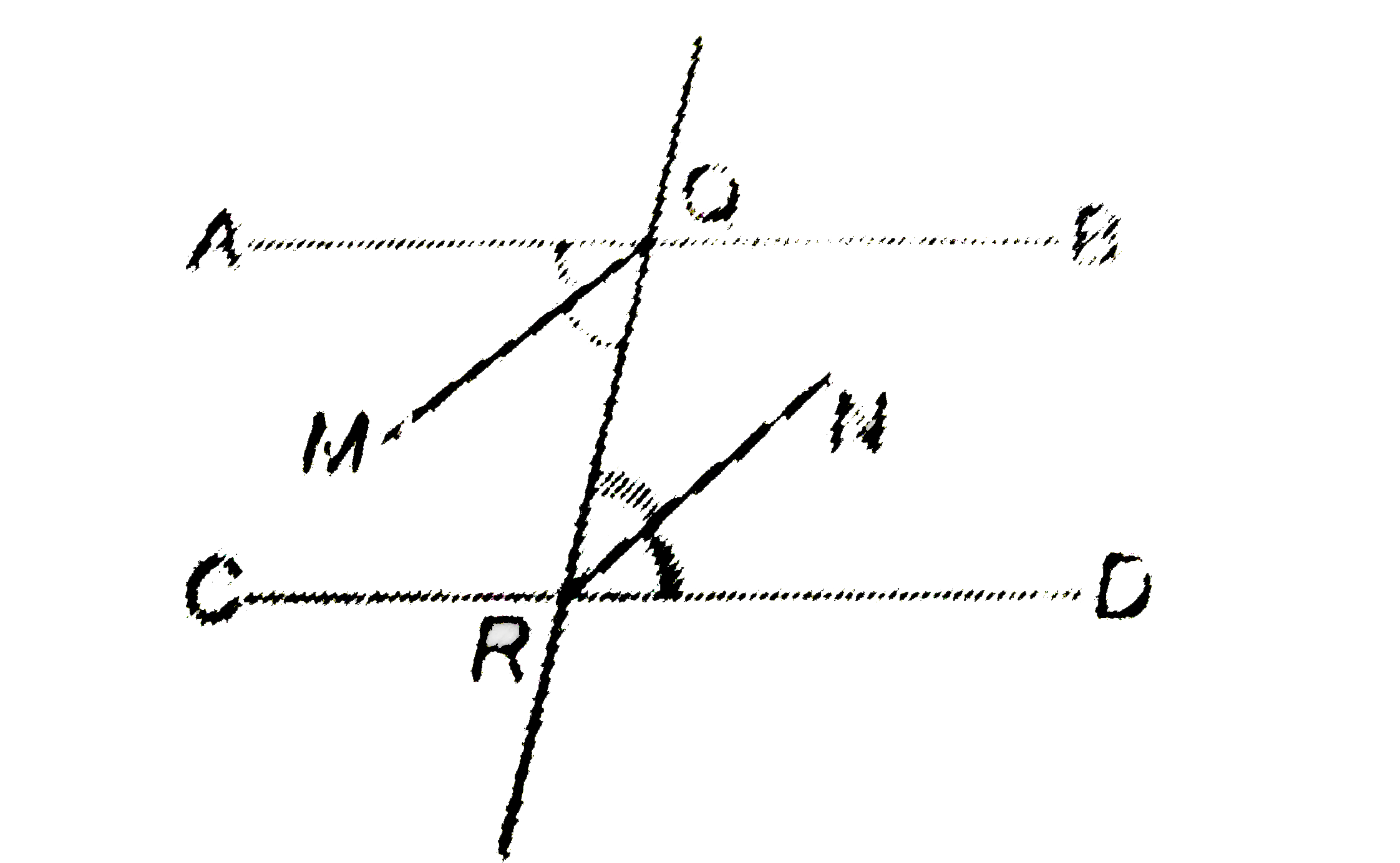
In the given figure, bisectors AP and BQ of the alternate interior angles are parallel, then show that l ||m.
Video Solution
Text Solution
Given. In the figure AP ||BQ, AP and BQ are the bisectors of alternate interior angles
∠CABand∠ABF
To show l||m
proof Since, AP ||BQ and t is transversal, therefore ∠PAB=∠ABQ [alternate interior angles ]
⇒ 2∠PAB=2∠ABQ [multiplying both sides by 2]
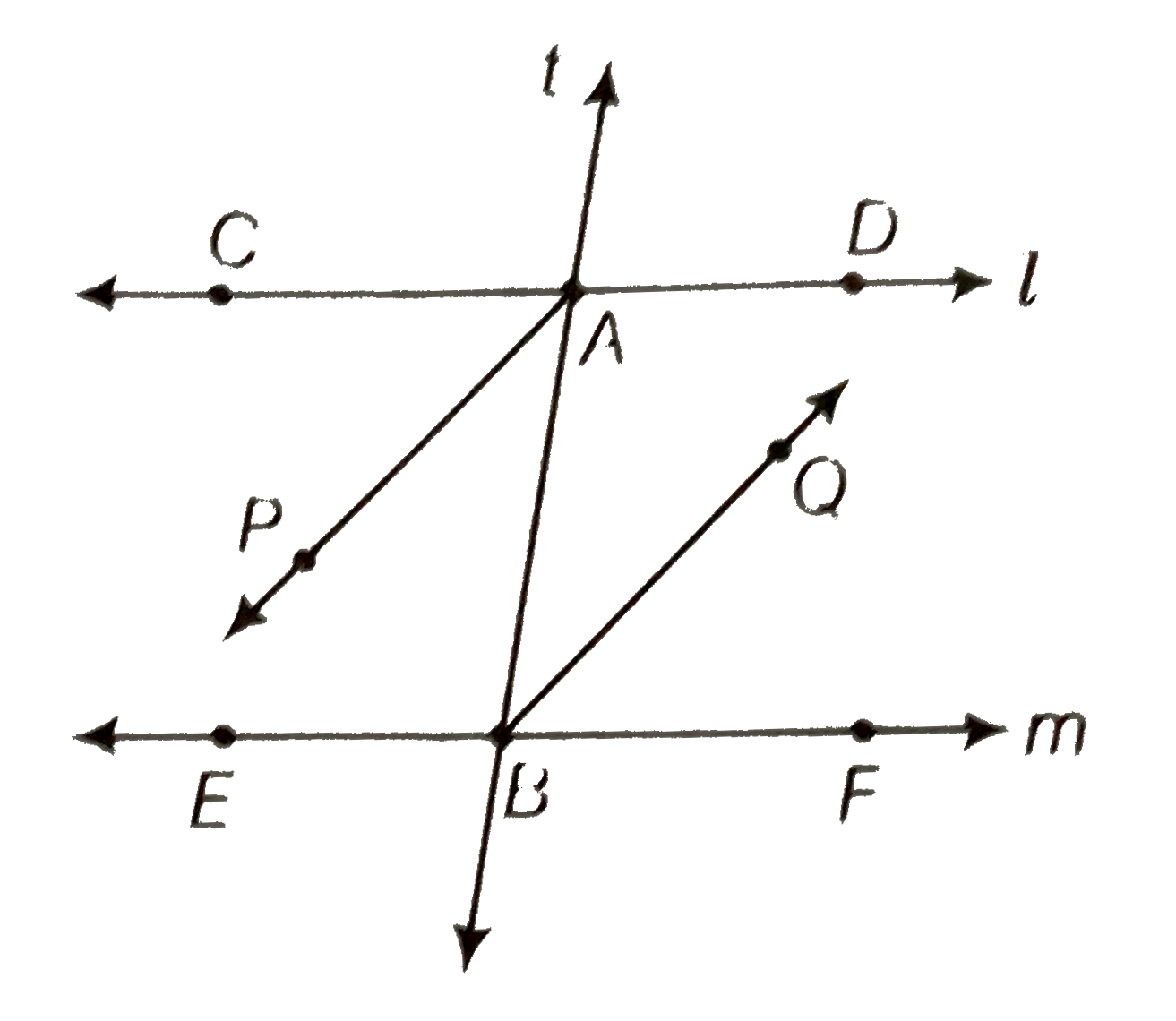
⇒ ∠CAB=∠ABF
So, alternate interior angles are equal.
We know that, if two alternate interior angles are equal, then lines are parallel.
Hence, l||m
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Alternate interior angles between parallel lines are equal
View SolutionIn the given figure l || m find x
View SolutionSum of co-interior angles between parallel lines is two right angles
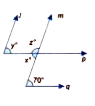
View SolutionIn the given figure l||mandp||q. Find the angle x,y, z
 View Solution
View SolutionIn the given figure, l||mandp||q. Find the angles x, y and z
 View Solution
View SolutionIn the given figure, l||mandp||q. Find the angles x, y, z and t.
 View Solution
View SolutionIn the following figure, AB||CD, QM and RN are bisectors of alternate angles AQR and QRD respectively. Show that QM||RN.
 View Solution
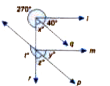
View SolutionIn the given figures below, decide whether l is parallel to m.
View SolutionProve that the bisectors of the interior angles of a rectangle form a square.
View SolutionIf the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosceles.
View Solution

