In the figure, DE || QR, AP and BP are bisectors of ∠EAB and ∠RBA, respectively. Find ∠APB.
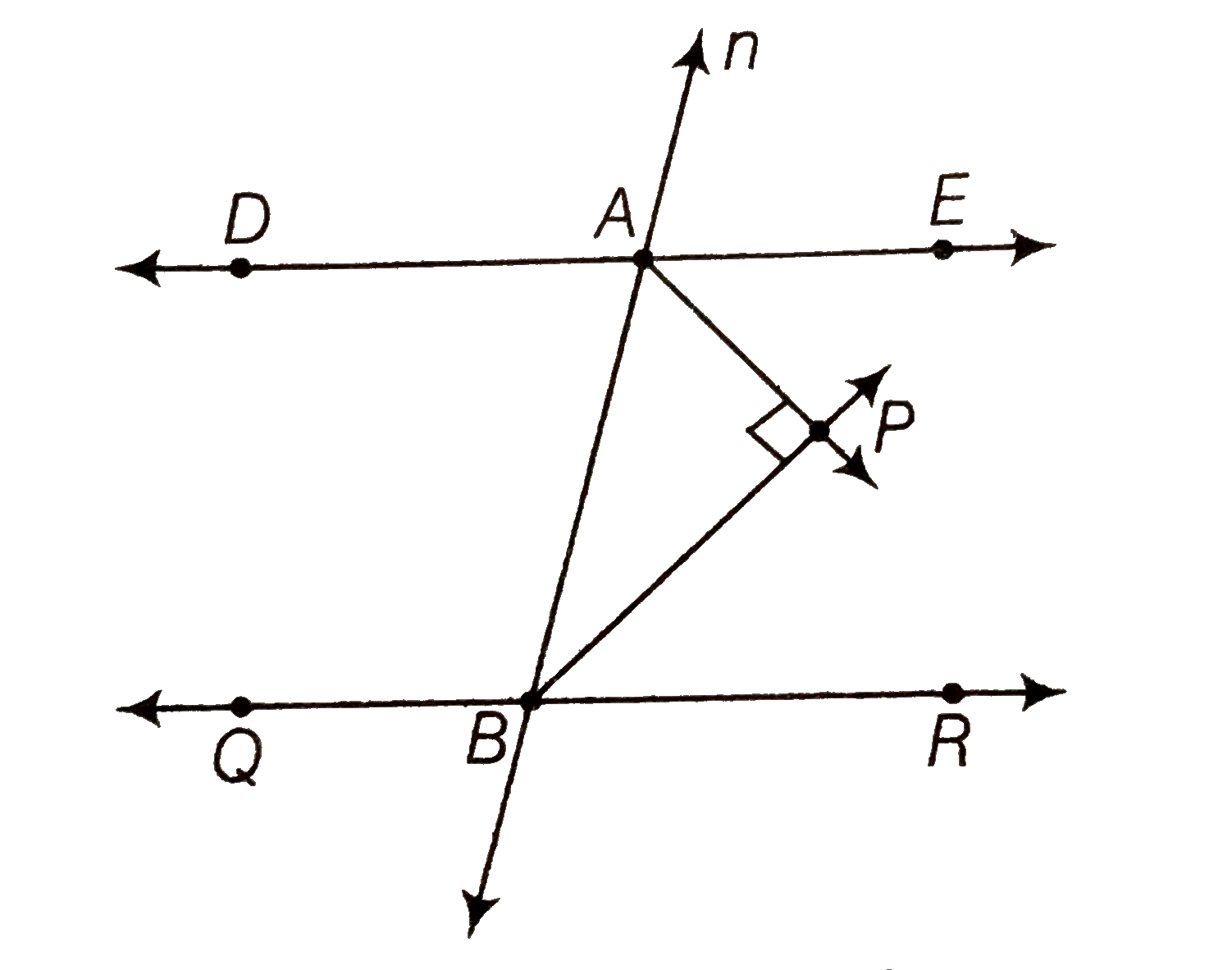
Given, DE∣∣ OR and AP and PB are the bisectors of ∠EAB and ∠RBA, respectively.
We know that. Interior angles on the same side of transversal are supplementary.
∴ ∠EAB+∠RBA=180∘
⇒ 12∠EAB+12∠RBA=180∘2 [dividing both sides by 2]
⇒ 12∠EAB+12∠RBA=90∘ ...(i)
Since, AP and BP are the bisectors of ∠EABand∠RBA, respectively.
∴ ∠BAP=12∠EAB ....(ii)
and ∠ABP=12∠RBA .........(iii)
On adding Eqs. (ii) and (iii), we get
∠BAP+∠ABP=12∠EAB+12∠RBA
From Eqs. (i),
⇒ ∠BAP+∠ABP=90∘ ....(iv)
In ΔAPB, ∠BAP+∠ABP+∠APB=180∘ [sum of all angles of a triangle is180∘]
⇒ 90∘+∠APB=180∘ [from Eq.(iv)]
⇒ ∠APB=180∘−90∘=90∘
Topper's Solved these Questions
Similar Questions
In the adjoining figure, OX and RX are the bisectors of the angle Q and R respectively of the triangle PQR. If XS⊥QR and XT⊥PQ.
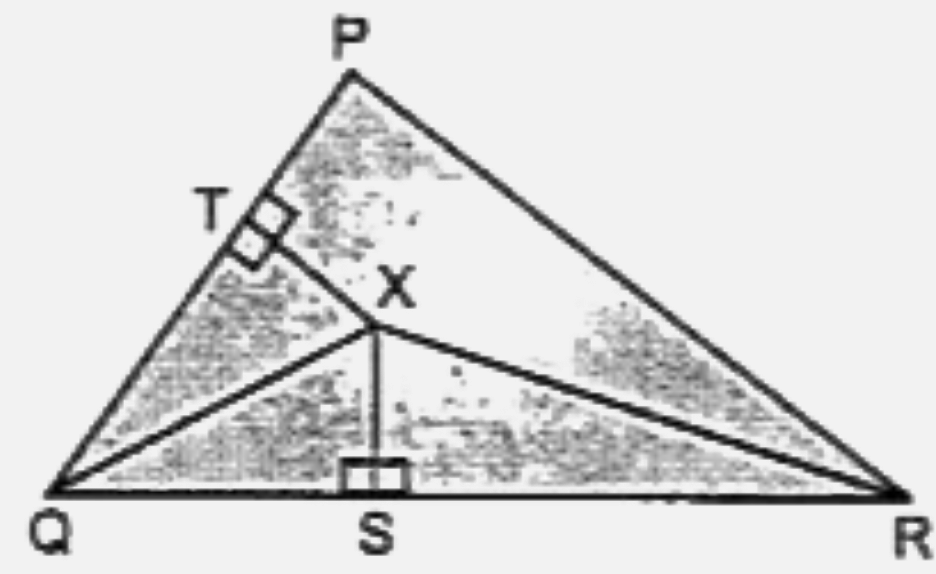
Prove that :
ΔXTQ≅ΔXSQView SolutionIn the adjoining figure, OX and RX are the bisectors of the angle Q and R respectively of the triangle PQR. If XS⊥QR and XT⊥PQ.
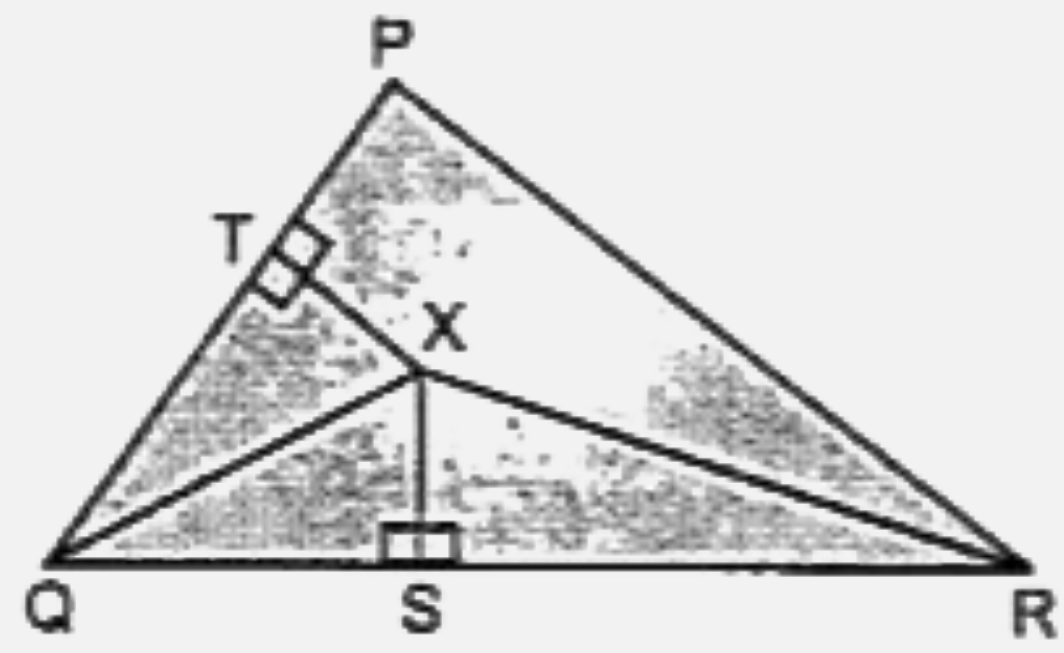
Prove that :
PX bisects angle P.View SolutionIn the adjoining figure, QX and RX are the bisectors of the angles Q and R respectively of the triangle PQR.
If XS⊥QRandXT⊥PQ, prove that :
ΔXTQ≅ΔXSQ
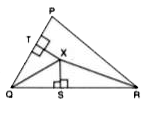 View Solution
View SolutionIn the given figure, XY || QR, PQ/XQ=7/3 and PR = 6.3 cm, find YR
View SolutionIn the following figure, AB||CD, QM and RN are bisectors of alternate angles AQR and QRD respectively. Show that QM||RN.
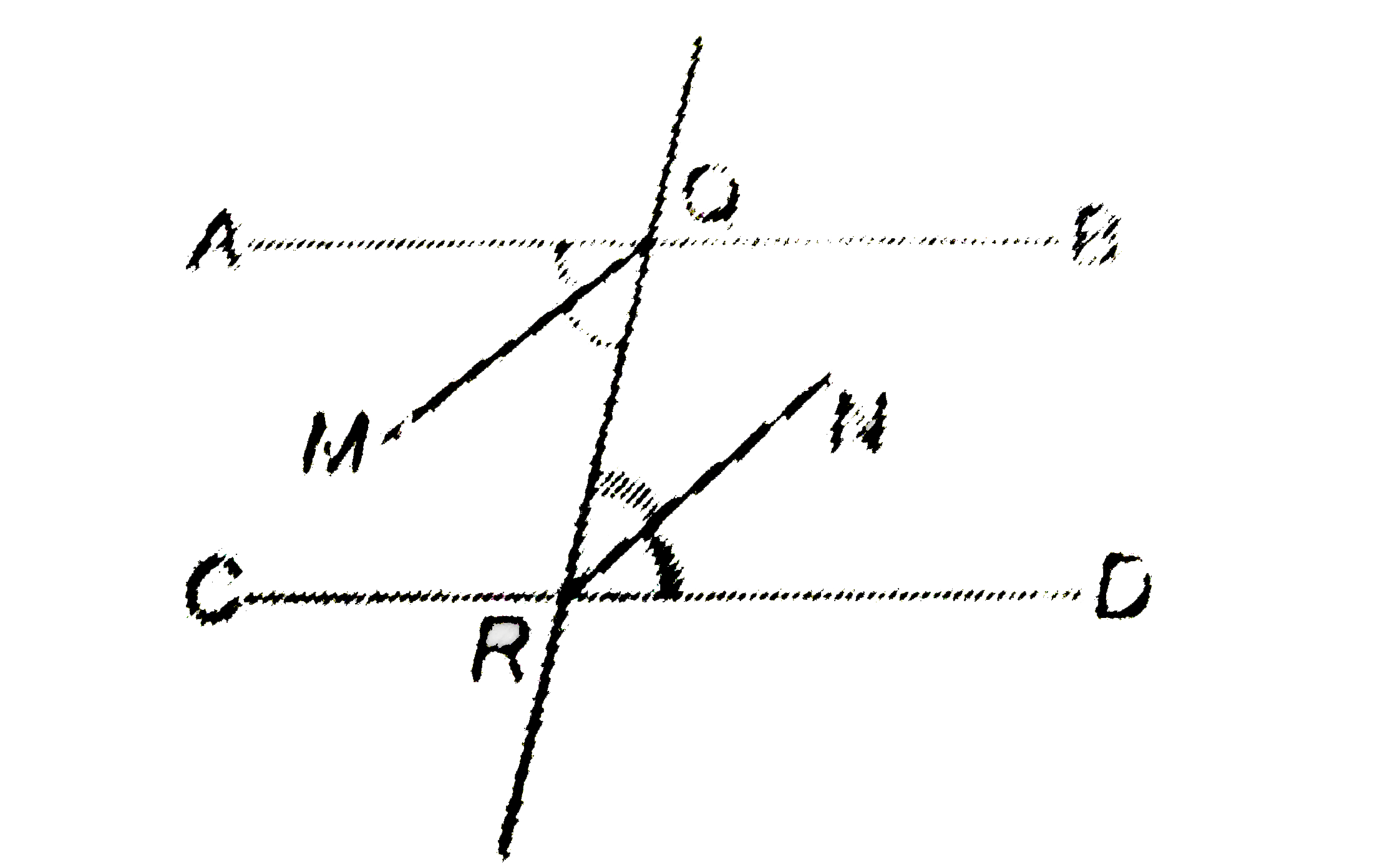 View Solution
View SolutionIn the following figure AB||CD,QM and RN are bisectors of corresponding angles PQB and QRD respectively. Show that QM ||RN
 View Solution
View SolutionIn the adjoining figure BO and CO are the bisectors of ∠CBD and ∠BCE respectively. If AC>AB, prove that OB>OC.
 View Solution
View SolutionIn the given figure if DE||BC, find the value of x.
View SolutionIn ΔABC,∠C=40∘,BQandAR are the angle bisectors of ∠Band∠A, respectively. Find ∠APQ.
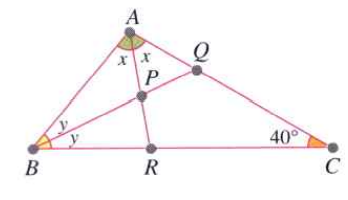 View Solution
View SolutionIn the given figure, if DE||AQ and DF||AR. Prove that EF||QR.
 View Solution
View Solution

