A ΔABC is right angled at A. L is a point on BC such that AL⊥ BC. Prove that ∠BAL=∠ACB.
To prove that ∠BAL = ∠ACB in triangle ABC, where triangle ABC is right-angled at A and AL is perpendicular to BC, we can follow these steps:
Step 1: Identify the Angles
We know that triangle ABC is right-angled at A, which means:
∠BAC=90∘
Let’s denote:
- ∠BAL as angle 1
- ∠ACB as angle 2
Step 2: Establish the Right Angles
Since AL is perpendicular to BC, we have:
∠ALB=90∘
Step 3: Compare Angles in Triangles
In triangle ABL:
- We have ∠BAL (angle 1) and ∠ALB (90°).
- In triangle ABC, we have ∠BAC (90°) and ∠ABC.
Step 4: Use the Angle Sum Property
For triangle ABL:
∠ABL+∠ALB+∠BAL=180∘
Substituting the known values:
∠ABL+90∘+∠BAL=180∘
This simplifies to:
∠ABL+∠BAL=90∘(Equation 1)
For triangle ABC:
∠ABC+∠ACB+∠BAC=180∘
Substituting the known values:
∠ABC+∠ACB+90∘=180∘
This simplifies to:
∠ABC+∠ACB=90∘(Equation 2)
Step 5: Equate the Two Equations
From Equation 1 and Equation 2, we have:
∠ABL+∠BAL=90∘
∠ABC+∠ACB=90∘
Since both sums equal 90°, we can equate them:
∠ABL+∠BAL=∠ABC+∠ACB
Step 6: Conclude the Proof
Since we already established that:
∠BAC=∠ALB
This means that:
∠BAL=∠ACB
Thus, we have proved that:
∠BAL=∠ACB
We know that triangle ABC is right-angled at A, which means:
∠BAC=90∘
Let’s denote:
- ∠BAL as angle 1
- ∠ACB as angle 2
Since AL is perpendicular to BC, we have:
∠ALB=90∘
In triangle ABL:
- We have ∠BAL (angle 1) and ∠ALB (90°).
- In triangle ABC, we have ∠BAC (90°) and ∠ABC.
For triangle ABL:
∠ABL+∠ALB+∠BAL=180∘
Substituting the known values:
∠ABL+90∘+∠BAL=180∘
This simplifies to:
∠ABL+∠BAL=90∘(Equation 1)
∠ABC+∠ACB+∠BAC=180∘
Substituting the known values:
∠ABC+∠ACB+90∘=180∘
This simplifies to:
∠ABC+∠ACB=90∘(Equation 2)
From Equation 1 and Equation 2, we have:
∠ABL+∠BAL=90∘
∠ABC+∠ACB=90∘
Since both sums equal 90°, we can equate them:
∠ABL+∠BAL=∠ABC+∠ACB
Since we already established that:
∠BAC=∠ALB
This means that:
∠BAL=∠ACB
Thus, we have proved that:
∠BAL=∠ACB
Topper's Solved these Questions
Similar Questions
ABC is a triangle in which AB=ACandD is a point on AC such that BC2=AC×CD.Prove that BD=BC.
View SolutionA triangle ABC is right angled at A. AL is drawn perpendicular to BC . Prove that ∠BAL=∠ACB.
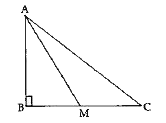
View SolutionABC is a triangle, right angled at B, M is a point on BC. Prove that :
AM2+BC2=AC2+BM2
 View Solution
View SolutionΔABC is right-angled at C. If AC=5cmandBC=12cm find the length of AB.
View SolutionIn isosceles triangle ABC, D is a point on the base BC produced. Prove that AD>AB.
 View Solution
View SolutionTriangle ABC is right angle at A. The points P and Q are on hypotenuse BC such that BP=PQ=QC.if AP=3andAQ=4, then length BC is equal to
View SolutionABC is a right angled triangle with ABC=90∘. D is any point on AB and DE is perpendicular to AC. Prove that:

If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.View SolutionIn ΔABC,AB=ACandD is a point an side AC such that AD = BD = BC . Show that : ∠ADB=108∘
View SolutionABC is a right triangle with AB = AC.If bisector of ∠A meet BC at D then prove that BC =2 AD .
View SolutionP is any point in the interior of a triangle ABC.
Prove that : PA+PB<AC+BCView Solution

