ABCD is a parallelogram in which BC is produced to E such that CE = BC. AE intersects CD at F.
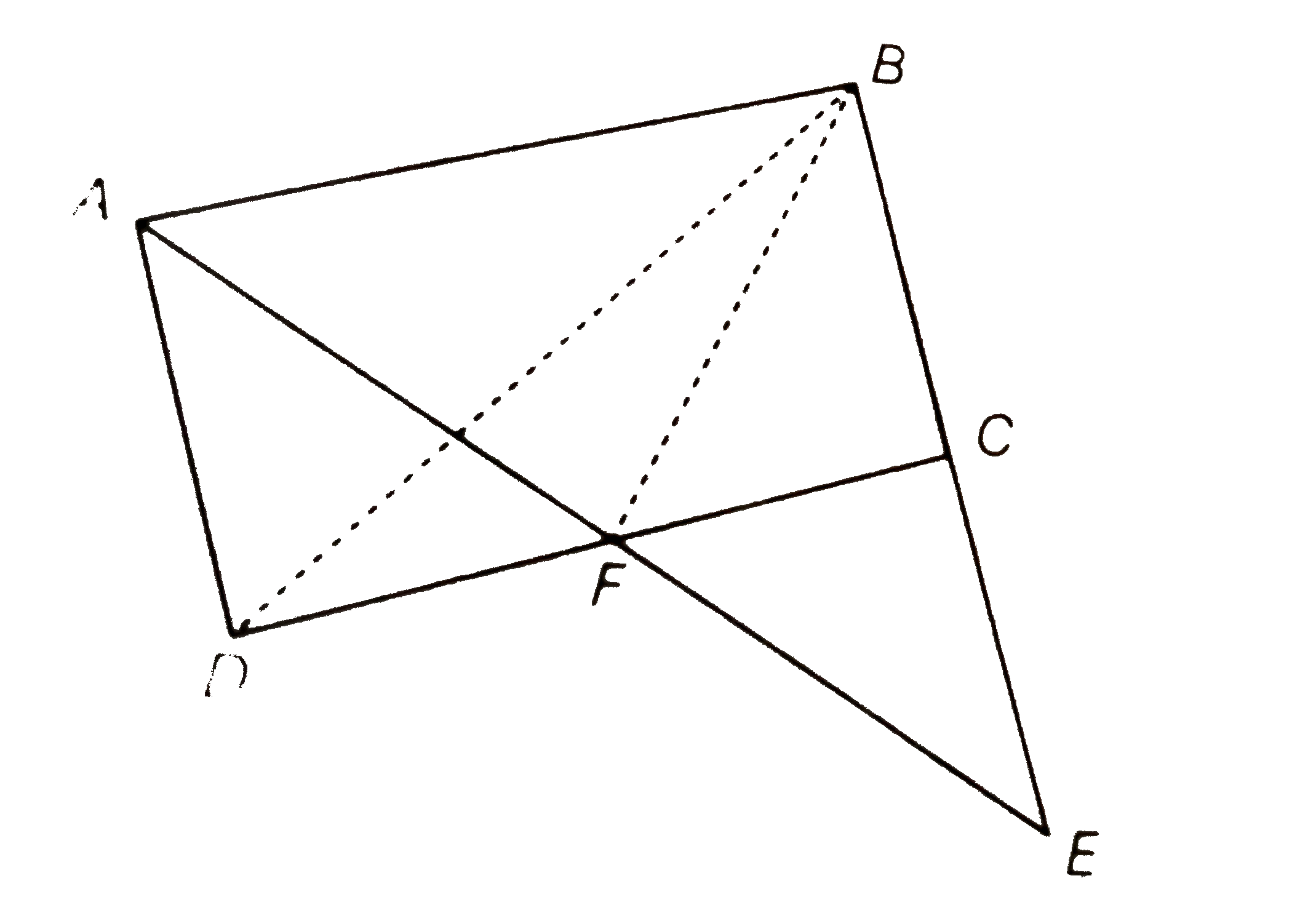
If ar(ΔDFB)=3cm2, then find the area of the parallelogram ABCD.
Given, ABCD is a parallelogram and CE = BC i.e., C is the mid-point of BE.
Also, ar(ΔDFB)=3cm2
Now, ΔADF and ΔDFB are on the same base DF and between parallels CD and AB. Then,
ar(ΔADF)=ar(ΔDFB)=3cm2 ...(i)
In ΔABE, by the converse of mid-point theorem,
EF=AF [since, C is mid-point of BE] ...(ii)
In ΔADF and ΔECF,
∠AFD=∠CFE [Vertically opposite angles]
AF=EF [from Eq. (ii)]
and ∠DAF=∠CEF
[since, BE∣∣AD and AE is transversal, then alternate interior angles are equal]
∴ ΔADF≅ΔECF [by ASA congruence rule]
Then, ar(ΔADF)=ar(ΔCFE) [since, congruent figures have equal area]
∴ ar(ΔCFE)=ar(ΔADF)=3cm2 [from Eq. (i)] ...(iii)
Now, in ΔBFE, C is the mid-point of BE then CF is median of
ΔBFE,
∴ ar(ΔCEF)=ar(ΔBFC) [since, median of a triangle divides it into two triangles of equal area]
⇒ ar(ΔBFC)=3cm2 ...(iv)
Now, ar(ΔBDC)=ar(ΔDFB)+ar(ΔBFC) [from Eqs. (i) and (iv)]
We know that, diagonal of a parallelogram divides it into two congruent triangles of equal areas.
∴ Area of parallelogram ABCD=2×Area of ΔBDC
=2×6=12cm2
Hence, the area of parallelogram ABCD is 12cm2 .
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.4 Long Answer Type Questions10videos
Areas of Parallelograms and Triangles
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.2 Very Short Answer Type Questions5videos
Areas of Parallelograms and Triangles
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.414videos
CIRCLES
Similar Questions
ABCD is a parallelogram in which BC is produced to E such that CE=BC and AE intersects CD at F.
If ar.(ΔDFB)=30cm2, find the area of parallelogram
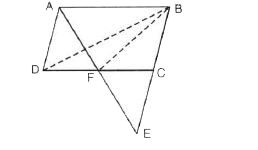 View Solution
View SolutionABCD is a parallelogram in which BC is produced to E such that CE=BC.AE intersects CD at F. Prove that ar ( ADF)= ar ( ECF). If the area of DFB=3 cm2, find the area of ABCD.
View SolutionThe given figure shows a parallelogram ABCD. E is a point in AD and CE produced meets BA produced at point F. If AE = 4 cm, AF = 8 cm and AB = 12 cm, find the perimeter of the parallelogram ABCD.
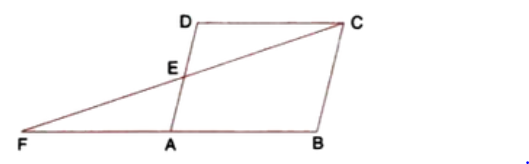 View Solution
View SolutionIn a parallelogram ABCD, point P lies in DC such that DP:PC= 3:2. If area of ΔDPB=30sq. cm, ffind the area of the parallelogram ABCD.
View SolutionABCD is a parallelogram. Find the ratio of the area of Δ ABC to the area of the parallelogram ABCD.
View SolutionIn the given figure, if the area of parallelogram ABCD is 40cm2, find the area of parallelogram ABEF
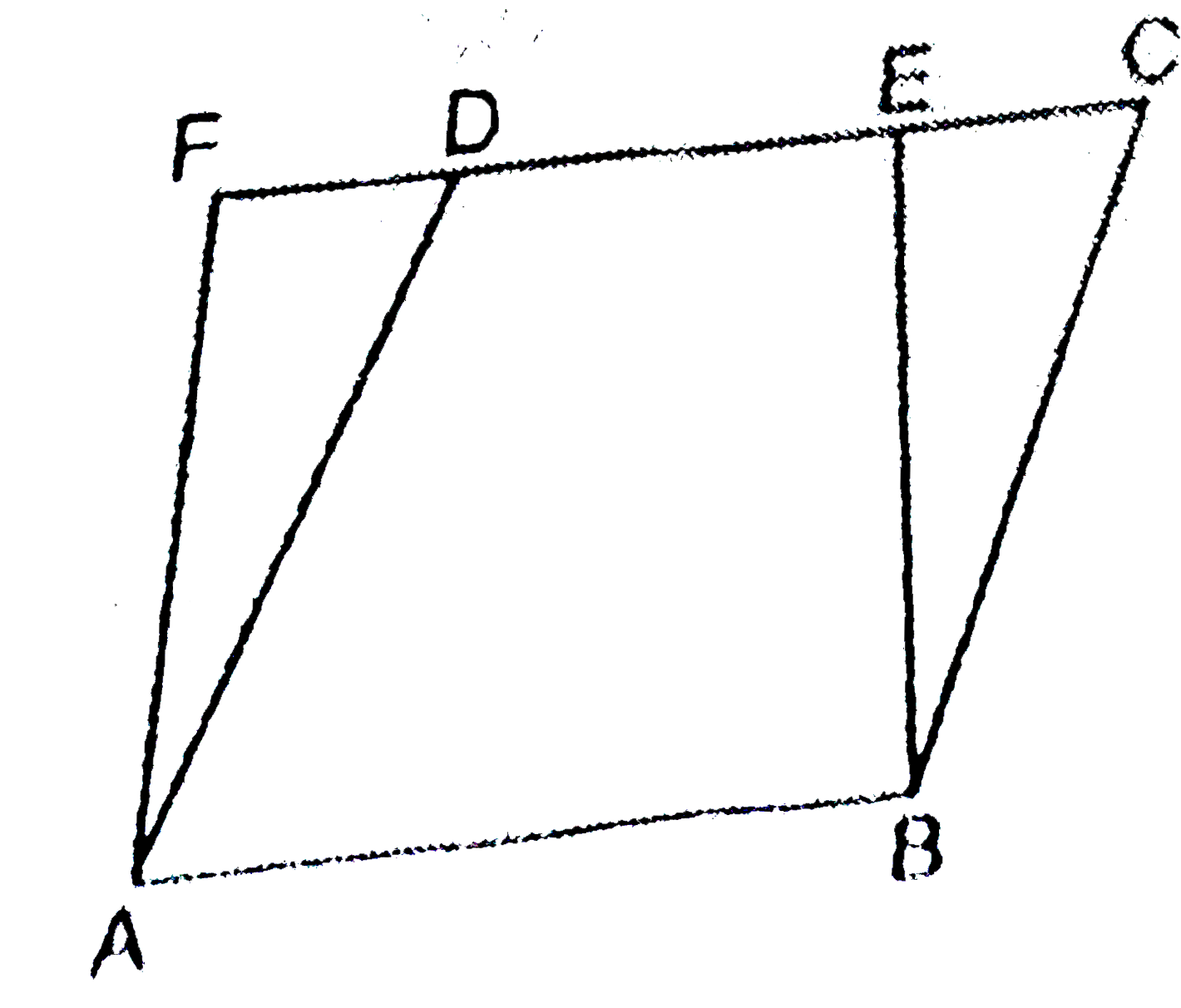 View Solution
View SolutionIn the parallelogram ABCD , the side AB is produced to the point X.so that BX= AB. The line DX cuts BC at E. Prove that :
Area (ΔAED)=2× area (ΔCEX).View SolutionABCD is a parallelogram having adjacent sides AB = 35 cm and BC = 28 cm . If the distance between its longer sides is 8 cm , find :
(i) the area of the parallelogram
(ii) the distance between its shorts sidesView SolutionABCD is a parallelogram whose adjacent sides AB = 48 cm and BC = 14 cm . One of its diagonds AC = 50 cm . Find :
(i) the area of the parallelogram ABCD.
(ii) the distance between the longer sides.
(iii) the distance between the shorter sides.View SolutionE is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE~ΔCFB .
View Solution

