X and Y are points on the side LN of the triangle LMN such that LX = XY = YN. Through X, a line is drawn parallel to LM to meet MN at Z (see figure). Prove that .
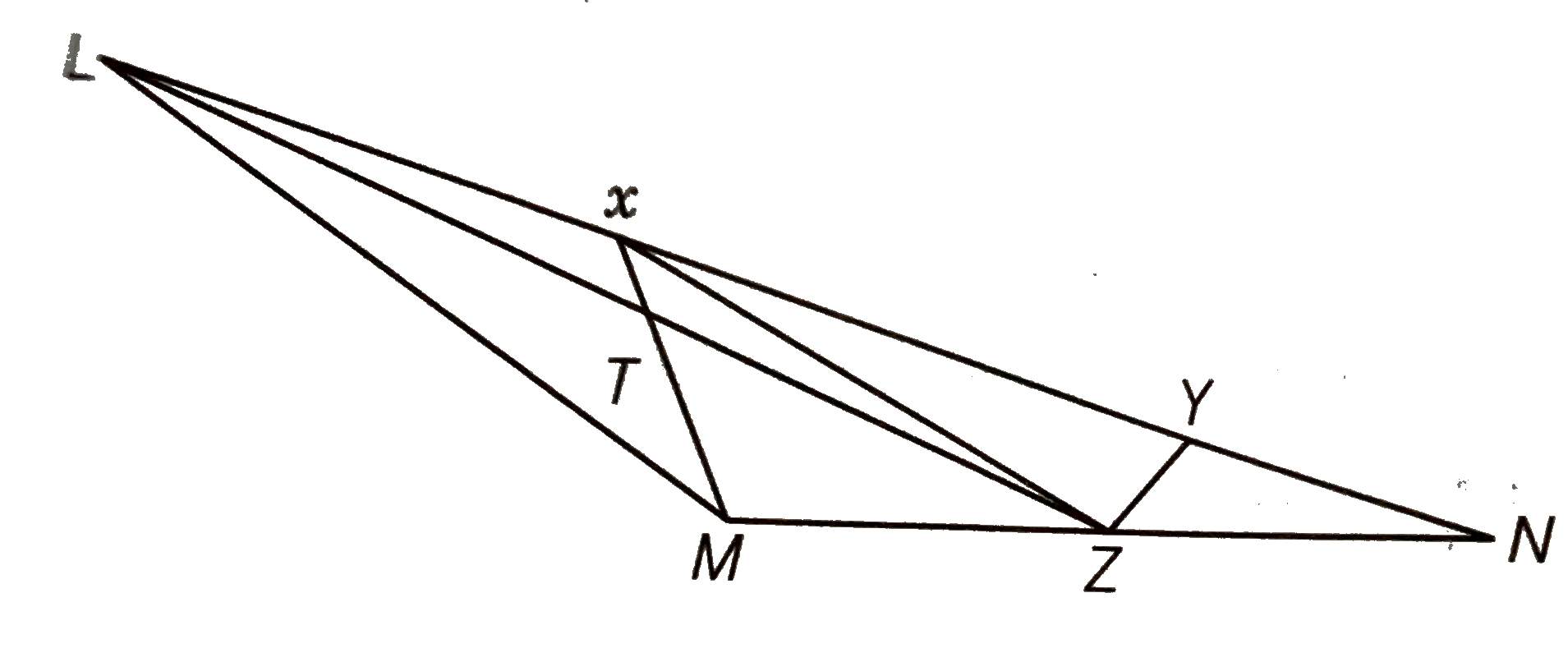
Given X and Y are points on the side LN such as that
LX = XY = YN and
To prove
Proof Since, and are on the same base XZ and between the same parallel lines LM and XZ.
Then, ...(i)
On adding both sides of Eq. (i), we get
Hence proved.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.4 Long Answer Type Questions10videos
Areas of Parallelograms and Triangles
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.2 Very Short Answer Type Questions5videos
Areas of Parallelograms and Triangles
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.414videos
CIRCLES
Similar Questions
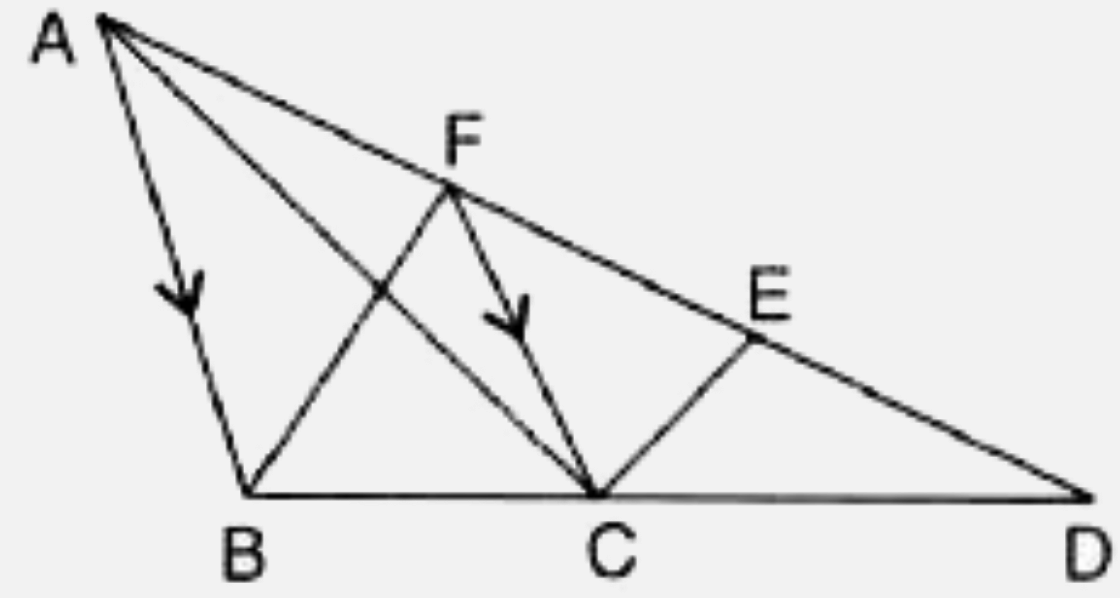
In the following figure, F and E are points on the side AD of the triangle ABD. Through F a line is drawn parallel to AB to meet BD at point C .
Prove that : ar (ΔACE)=ar (quad . BCEF )
 View Solution
View SolutionIn triangle ABC, D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F. Prove that BDEF is a parallelogram. If AB = 16 cm, AC = 12 cm and BC = 18 cm, find the perimeter of the parallelogram BDEF.
View SolutionIn triangle ABC, D and E are points on side AB such that AD = DE = EB. Through D and E, lines are drawn parallel to BC which meet side AC at points F and G respectively. Through F and Glines are drawn parallel to AB which meet side BC at points M and N respectively.
Prove that : BM = MN = NC.View SolutionABC is a triangle A line is drawn parallel to BC to meet AB and AC in D and E respectively. Prove that the median through A bisects DE.
View SolutionD and F are the mid-points of sides AB and AC of a triangle ABC. A line through F and parallel to AB meets BC at point E.
Prove that BDFE is a parallelogramView SolutionD and F are the mid-points of sides AB and AC of a triangle ABC. A line through F and parallel to AB meets BC at point E.
Find AB, if EF=4.8cm.View SolutionLex X by any point on the side BC of a triangle ABC. If XM, XN are drawn parallel to BA and CA meeting CA, BA in M, N respectively; MN meets BC produced in T, prove that TX2=TB x TC
View SolutionP is a point on the bisector of ∠ABC .If the line through P, parallel to BA meet at Q ,prove that ΔBPQ is an isosceles triangle.
View SolutionIn parallelogram ABCD, E is mid-point of CD and through D, a line is drawn parallel to EB to meet CB produced at point G and to cut AB at point F. Prove that :
DG = 2EBView SolutionP is the mid-point of the side CD of a parallelogram ABCD. A line through C parallel to PA intersects AB at Q and DA produced at R. Prove that DA = AR and CQ = QR.
View Solution

