Convert the given frequency distribution into a continuouos grouped frequency distribution.
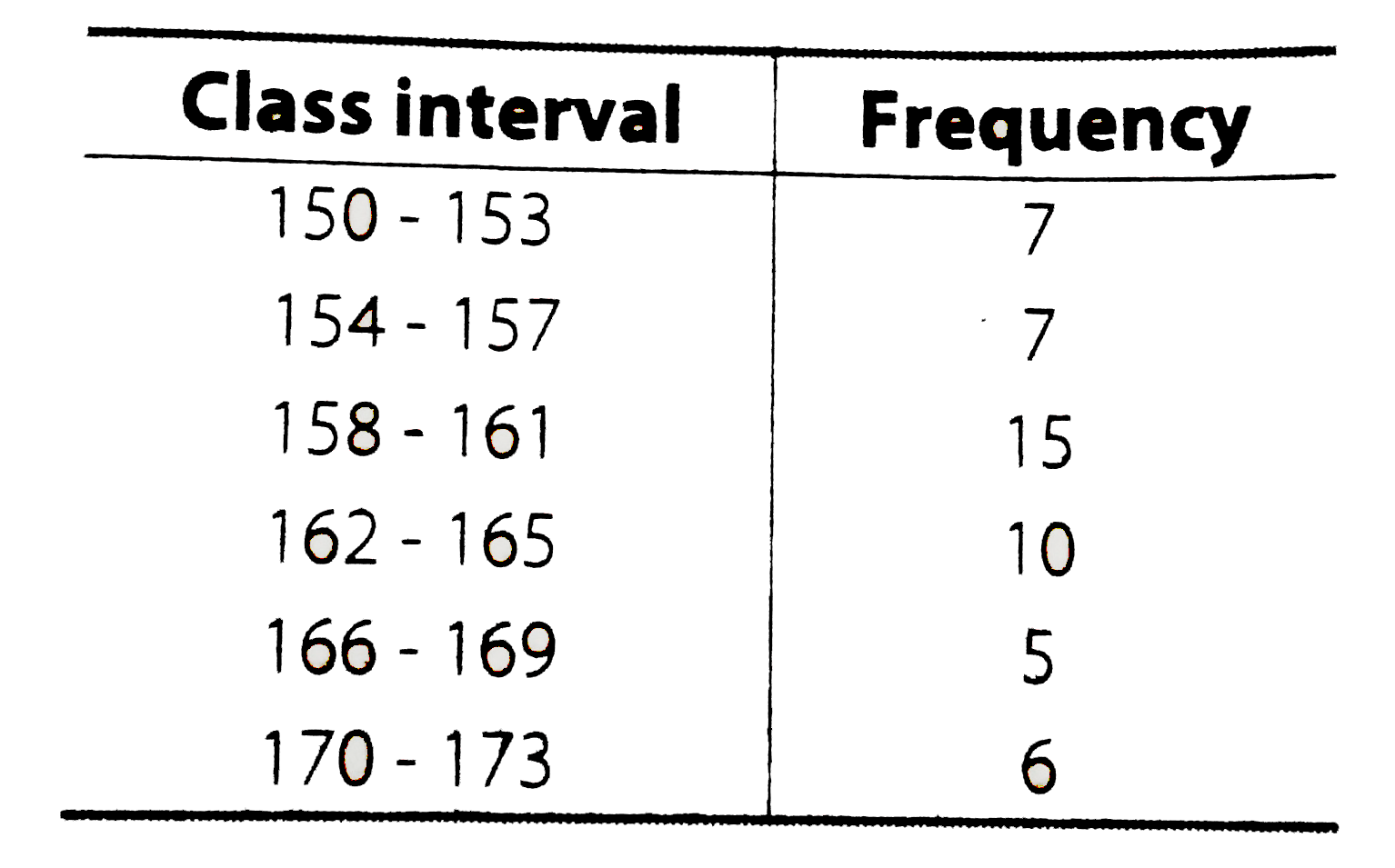
In which intervals would 153.5 and 157.5 be included?
Video Solution
Text Solution
It is clear that, the given table is in exclusive (discontinous) from. So, we first convert it into exclusive form.
Now, consider the classes 150-153, 154-157
∴ Lower limt of 154-157=154
and upper limit of 150-153=153
Required difference =154-153=1
So, half the difference =1/2=0.5
So, we subtract 0.5 from each lower limit and add 0.5 to each upper limit.
The table for continous grouped frequency distribution is given below.

Thus, 153.5 and 157.5 would use in the class intervals 153.5−157.5 and 157.5−161.5, respectively.
|
Topper's Solved these Questions
- STATISTICS AND PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ANSWER TYPE QUESTIONS
12 Videos
- STATISTICS AND PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - VERY SHORT ANSWER TYPES QUESTIONS
10 Videos
- QUADRILATERALS BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - QUADRILATERALS EXERCISE - LONG ANSWER TYPE QUESTIONS
18 Videos
- TRIANGLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - LONG ANSWER TYPE QUESTIONS
21 Videos
Similar Questions
Cumulative Frequency Distribution
View SolutionExplain the difference between a frequency distribution and a cumulative frequency distribution.
View SolutionQuartile deviation for a frequency distribution is
View SolutionFind the mean for the following frequency distribution :
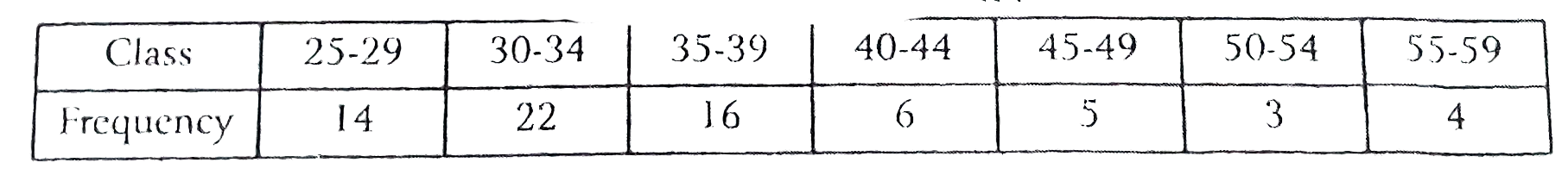
View SolutionFind the mode of the following frequency distribution

View SolutionFind the mode of the following frequency distribution :
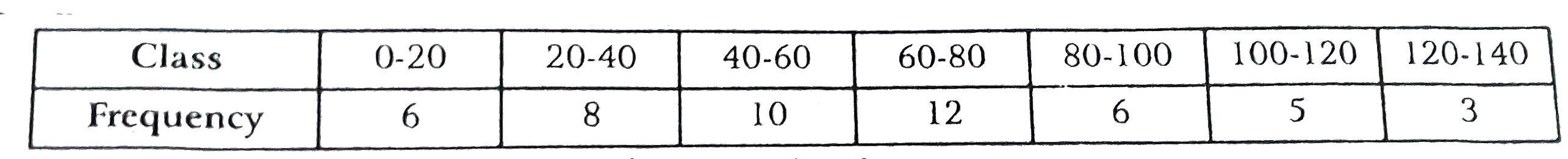
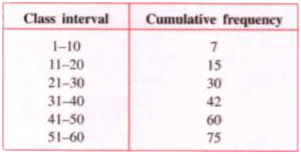
View SolutionContruct a cumulative frequency distributions table from the following frequency table:

View SolutionContruct a cumulative frequency distributions table from the following frequency table:
View SolutionThe mode for the following frequency distribution :

View SolutionFind the median for the following frequency distribution:
View Solution
