Derive the expression for the torque τ acting on a rectangular current loop of area A placed in a uniform magnetic field B. Show that →τ=→m×→B where →m is the moment of the current loop given by →m=→IA.
To derive the expression for the torque τ acting on a rectangular current loop of area A placed in a uniform magnetic field B, we will follow these steps:
Step 1: Define the Current Loop and Magnetic Field
Consider a rectangular current loop with area A and a current I flowing through it. The loop is placed in a uniform magnetic field →B. Let the loop be oriented such that its sides are parallel to the axes.
Step 2: Calculate the Forces on the Loop
The forces acting on the segments of the loop can be analyzed. The force →F on a segment of wire carrying current I in a magnetic field →B is given by:
→F=I→L×→B
where →L is the length vector of the wire segment.
For the segments BC and AD, the angle α between the current direction and the magnetic field will determine the force. The forces on these segments will be equal in magnitude but opposite in direction.
Step 3: Analyze the Forces on Segments AB and CD
For segments AB and CD, if we assume they are perpendicular to the magnetic field, the force on each segment can be calculated as:
→FAB=I⋅L⋅B⋅sin(90∘)=I⋅L⋅B
where L is the length of the segment.
Step 4: Calculate the Torque
The torque τ on the loop due to these forces can be calculated using the formula:
τ=Force×Perpendicular distance
The perpendicular distance from the line of action of the force to the axis of rotation (which we can take as the center of the loop) is given by:
Perpendicular distance=A2sinθ
where θ is the angle between the magnetic field and the normal to the plane of the loop.
Thus, the torque can be expressed as:
τ=F⋅d=(I⋅L⋅B)⋅(Asinθ)
Step 5: Express Torque in Terms of Area
If A is the area of the loop, we can rewrite the torque as:
τ=I⋅(L⋅A)⋅B⋅sinθ
Here, L⋅A represents the area of the loop.
Step 6: Define the Magnetic Moment
The magnetic moment →m of the loop is defined as:
→m=N⋅I⋅A
where N is the number of turns in the loop.
Step 7: Final Expression for Torque
Finally, we can express the torque in vector form:
→τ=→m×→B
This shows that the torque acting on a current loop in a magnetic field is given by the cross product of the magnetic moment and the magnetic field.
Conclusion
Thus, we have derived the expression for the torque acting on a rectangular current loop in a magnetic field:
→τ=→m×→B
Consider a rectangular current loop with area A and a current I flowing through it. The loop is placed in a uniform magnetic field →B. Let the loop be oriented such that its sides are parallel to the axes.
The forces acting on the segments of the loop can be analyzed. The force →F on a segment of wire carrying current I in a magnetic field →B is given by:
→F=I→L×→B
where →L is the length vector of the wire segment.
For segments AB and CD, if we assume they are perpendicular to the magnetic field, the force on each segment can be calculated as:
→FAB=I⋅L⋅B⋅sin(90∘)=I⋅L⋅B
where L is the length of the segment.
The torque τ on the loop due to these forces can be calculated using the formula:
τ=Force×Perpendicular distance
The perpendicular distance from the line of action of the force to the axis of rotation (which we can take as the center of the loop) is given by:
Perpendicular distance=A2sinθ
where θ is the angle between the magnetic field and the normal to the plane of the loop.
τ=F⋅d=(I⋅L⋅B)⋅(Asinθ)
If A is the area of the loop, we can rewrite the torque as:
τ=I⋅(L⋅A)⋅B⋅sinθ
Here, L⋅A represents the area of the loop.
The magnetic moment →m of the loop is defined as:
→m=N⋅I⋅A
where N is the number of turns in the loop.
Finally, we can express the torque in vector form:
→τ=→m×→B
This shows that the torque acting on a current loop in a magnetic field is given by the cross product of the magnetic moment and the magnetic field.
Thus, we have derived the expression for the torque acting on a rectangular current loop in a magnetic field:
→τ=→m×→B
Topper's Solved these Questions
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - C.B.S.E.CLASS-XII PHYSICS (THEORY) [SET-I] (SECTION-A)5videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTIONS-B4videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTION-C50videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D6videos
SAMPLE PAPER 2019
Similar Questions
Knowledge Check
- Question 1 - Select One
A current carrying loop is placed in a uniform magnetic field. The torque acting on it does not depend upon
Aarea of loopBvalue of currentCmagnetic fieldDNone of these
Obtain the expression for the torque →τ experienced by an electric dipole of dipole moment →p in a uniform electric field , →E
View Solution(a) Derive the expression for the torque acting on a current carrying placed in a magnetic field.
(b) Explain the significance of a radial magnetic when current carrying coil is kept in it.View SolutionA semi circular current loop is placed in an uniform magnetic field of 1 tesla as shown. If the radius of loop is 1 m, the magnetic force on the loop is
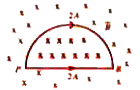 View Solution
View Solution(a) Write the expression for the force, →F, acting on a charged particle of charge 'q', moving with a velocity →V in the presence of both electric field →E and magnetic field →B. Obtain the condition under which the particle moves undeflected through the fields.
(b) A rectangular loop of size l×b carrying a steady current I is placed in a uniform magnetic field →B. Prove that the torque →τ acting on the loop is given by
→τ=→m×→B, where →m is the magnetic moment of the loop.View SolutionA triangular loop of side l carries a current l. It is placed in a magnetic field B such that the plane of the loop is in the direction of B. The torque on the loop is
View SolutionA triangular loop of side l carries a current I. It is placed in a magnetic field B such that the plane of the loop is in the direction of B. The torque on the loop is
View Solution(a) Two straight long parallel conductors carry currents I1 and I2 in the same direction. Deduce the expression for the firce per unit length between them.
Depict the pattern of magnetic field lines around them.
(b) A rectangular current carrying loop EFGH is kept in a uniform magnetic field as shown in the figure.
(i) What is the direction of the magnetic moment of the current loop ?
(ii) What is the torque acting on the loop (A) maximum, (B) zero ?
 View Solution
View Solution

