A convex lens, of focal length 25 cm, and a concave mirror, of radius of curvature 20 cm. are placed co-axially 40 cm aprat from each other. An incident beam, parallel to the principal axis, is incident on the convex lens. Find the position and nature of the image formed by this combination.
To solve the problem step by step, we will analyze the situation involving the convex lens and the concave mirror.
Step 1: Identify the parameters
- Focal length of the convex lens, fL=+25cm
- Radius of curvature of the concave mirror, R=−20cm (negative because it is a concave mirror)
- Focal length of the concave mirror, fM=R2=−202=−10cm
- Distance between the lens and mirror, d=40cm
Step 2: Find the image formed by the convex lens
Since the incident beam is parallel to the principal axis, the image formed by the convex lens will be at its focal point.
Using the lens formula:
1fL=1vL−1uL
Where:
- uL=−∞ (object distance for a parallel beam)
- fL=+25cm
Thus, the image distance vL can be calculated as:
125=1vL−0⟹vL=+25cm
Step 3: Determine the position of the image relative to the mirror
The image formed by the convex lens is located 25 cm to the right of the lens. Since the lens and mirror are 40 cm apart, the distance from the lens to the mirror is 40 cm. Therefore, the distance from the mirror to the image is:
dmirror=40−25=15cm
This means the image is 15 cm in front of the concave mirror.
Step 4: Treat the image from the lens as the object for the concave mirror
Now, we will treat this image as the object for the concave mirror. The object distance uM for the concave mirror is:
uM=−15cm(negative because it is in front of the mirror)
Step 5: Use the mirror formula to find the image distance for the mirror
Using the mirror formula:
1fM=1vM+1uM
Substituting the values:
1−10=1vM+1−15
Rearranging gives:
1vM=1−10+115
Finding a common denominator (30):
1vM=−3+230=−130
Thus,
vM=−30cm
Step 6: Interpret the result
The negative sign indicates that the image is formed on the same side as the object for the mirror, which means it is a real image.
Conclusion
The final image formed by the combination of the convex lens and concave mirror is located 30 cm in front of the concave mirror. The nature of the image is:
- Real
- Inverted
- Diminished
- Focal length of the convex lens, fL=+25cm
- Radius of curvature of the concave mirror, R=−20cm (negative because it is a concave mirror)
- Focal length of the concave mirror, fM=R2=−202=−10cm
- Distance between the lens and mirror, d=40cm
Since the incident beam is parallel to the principal axis, the image formed by the convex lens will be at its focal point.
1fL=1vL−1uL
Where:
- uL=−∞ (object distance for a parallel beam)
- fL=+25cm
125=1vL−0⟹vL=+25cm
The image formed by the convex lens is located 25 cm to the right of the lens. Since the lens and mirror are 40 cm apart, the distance from the lens to the mirror is 40 cm. Therefore, the distance from the mirror to the image is:
dmirror=40−25=15cm
This means the image is 15 cm in front of the concave mirror.
Now, we will treat this image as the object for the concave mirror. The object distance uM for the concave mirror is:
uM=−15cm(negative because it is in front of the mirror)
Using the mirror formula:
1fM=1vM+1uM
Substituting the values:
1−10=1vM+1−15
Rearranging gives:
1vM=1−10+115
Finding a common denominator (30):
1vM=−3+230=−130
Thus,
vM=−30cm
The negative sign indicates that the image is formed on the same side as the object for the mirror, which means it is a real image.
The final image formed by the combination of the convex lens and concave mirror is located 30 cm in front of the concave mirror. The nature of the image is:
- Real
- Inverted
- Diminished
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - C.B.S.E.CLASS-XII PHYSICS (THEORY) [SET-I] (SECTION-A)
5 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTIONS-B
4 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTION-C
50 Videos
- SAMPLE PAPER 2019BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
A convex lens of focal length 20cm and a convex mirror of focal length 10cm are placed co-axially 50cm apart from each other. An incident beam parallel to its principal axis is incideent on the convex lens. Locate the position of final image formed due to the combination.
View SolutionA convex lens of focal length 20cm is placed co-axially with a convex mirror of radius of curvature 20cm. The two are kept 15cm apart from each other. A point object is placed 60cm in front of the convex lens. Find the position of the image formed by the combination.
View SolutionA convex lens of focal length 20cm is placed coaxilly with a convex mirror of radius of curvature 20 cm. The two are kept 15 cm apart. A point object is placed 40 cm in front of the convex lens. Find the position of the image formed by this combination. Draw the ray diagram showing the image formation.
View SolutionThe focal length of a convex mirror is 20 cm its radius of curvature will be
View SolutionA converging lens of focal length 20 cm and a converging mirror of focal length 10 cm are placed 60 cm apart with common principal axis. A point source is placed in between the lens and the mirror at a distance of 50 cm from the lens. Find the locations of the images formed.
View SolutionA convex lens of focal length 20 cm and a concave lens of focal length 10 cm are placed 10 cm apart with their principal axes coinciding. A beam of light travelling parallel to the principal axis and having a beam diameter 5.0 mm, is incident on the combination. Show that the emergent beam is parallel to the incident one. Find the beam diameter of the emergent beam.
View SolutionA convex lens of focal length 100 cm and a concave lens of focal length 10 cm are placed coaxialiy at a separation of 90 cm. If a parallel beam of light is incident on convex lens, then after passing through the two lenses the beam
View SolutionA converging lens of focal length 15 cm and a converging mirror of focal length 10 cm are placed 50 cm apart with common principal axis. A point source is placed in between the lens and the mirror at a distance of 40 cm from the lens. Find the locations of the two images formed.
View SolutionA concave mirror of focal length 10cm and a convex mirror of focal length 15cm are placed facing each other 40cm apart. A point object is placed between the mirrors, on their common axis and 15cm from the concave mirror. Find the position and nature of the image produced by successive reflections, first at the concave mirror and then at the convex mirror.
View SolutionA convex lens of focal length 10 cm and a concave lens of same focal length in value are placed co-axially at a separation of 20 cm as shown in figure. A point object is at infinity on the principal axis. Take the optic center of convex lens as origin of co ordinate system and the principal axis as x-axis as shown in figure.
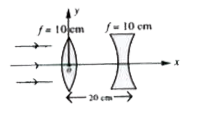
In the initial positin (as given in the passage ) if the concave lens has a velocit of 9 cm/s towards the convex lens, the velocity of the final image will be
View Solution
