In the figure DE is parallel to BC and ADDB=23 if AE = 3.7 cm find EC.
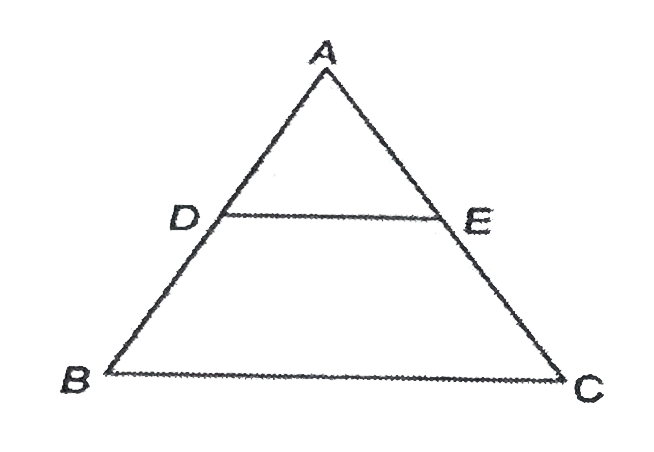
The correct Answer is:EC = 5.55 cm
Step by step video & image solution for In the figure DE is parallel to BC and (AD)/(DB) = 2/3 if AE = 3.7 cm find EC. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Eercise 6b1videos
TRIANGLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Exercise 6b29videos
TRIANGLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Problems From NCERT/ Exemplar14videos
TRIANGLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions4videos
STATISTICS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions5videos
VOLUME AND SURFACE AREA OF SOLIDS
Similar Questions
In the given figure, DE||BC and ADDB=23if AE=3.7 cm , find EC.
 View Solution
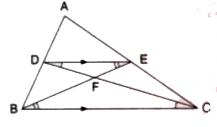
View SolutionIn the given figure, ABC is a triangle. DE is parallel to BC and ADDB=32

Determine the ratios and ADABView SolutionIn the given figure, ABC is a triangle. DE is parallel to BC and ADDB=32

Prove that ΔDEF is similar to ΔCBF.Hence, find EFFB.View SolutionIn the given figure, ABC is a triangle. DE is parallel to BC and ADDB=32

What is the ratio of the areas of ΔDEF and ΔBFC ?View SolutionIn the given figure, DE is parallel to the base BC of triangle ABC and AD: DB = 5: 3. Find the ratio :
ADAB and then DEBCView SolutionIn the given figure, DE is parallel to the base BC of triangle ABC and AD: DB = 5: 4. Find the ratio :

Area of ΔDEFArea ofΔBFCView SolutionIn the given figure, AB and DE are perpendiculars to BC. If AB = 9 cm, DE = 3 cm and AC = 24 cm, calculate AD.
 View Solution
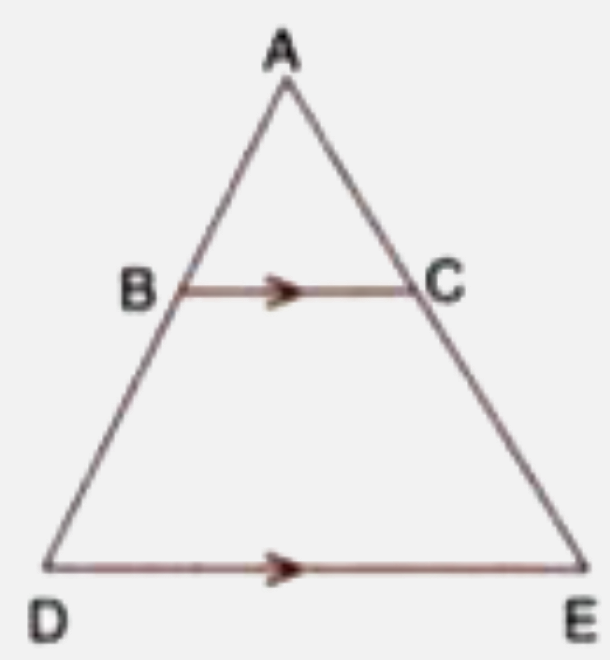
View SolutionIn the given figure, BC is parallel to DE. Area of triangle ABC=25cm2, Area of trapezium BCED=24cm2andDE=14cm. Calculate the length of BC.
Also, find the area of triangle BCD.
 View Solution
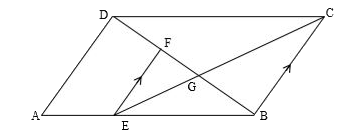
View SolutionIn the figure given below, ABCD is a parallelogram. E is a point on AB. CE intersects the diagonal BD at G and EF is parallel to BC.
If AE : EB = 1 : 2 find
EF : AD
 View Solution
View SolutionIn the given figure, ABCD is a trapezium with angle C=120∘,DC=28 cm and BC=40 cm. Find :
(ii) ADView Solution

