In ∆DEW, AB || EW. If AD = 4 cm, DE = 12 cm and DW = 24 cm, then find the value of DB.
The correct Answer is:8 cm
To solve the problem, we will use Thales' theorem, which states that if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally.
1. Identify the Given Values:
- AD=4cm
- DE=12cm
- DW=24cm
- Let DB=xcm
- Then, BW=DW−DB=24−xcm
- Let AE=DE−AD=12−4=8cm
2. Apply Thales' Theorem:
According to Thales' theorem:
ADAE=DBBW
Substituting the known values:
48=x24−x
3. Cross-Multiply to Solve for x:
Cross-multiplying gives:
4(24−x)=8x
Expanding the left side:
96−4x=8x
4. Combine Like Terms:
Adding 4x to both sides:
96=8x+4x
96=12x
5. Solve for x:
Dividing both sides by 12:
x=9612=8cm
6. Conclusion:
Therefore, the value of DB is 8cm.
Final Answer:
DB=8cm
- AD=4cm
- DE=12cm
- DW=24cm
- Let DB=xcm
- Then, BW=DW−DB=24−xcm
- Let AE=DE−AD=12−4=8cm
According to Thales' theorem:
ADAE=DBBW
Substituting the known values:
48=x24−x
Cross-multiplying gives:
4(24−x)=8x
Expanding the left side:
96−4x=8x
Adding 4x to both sides:
96=8x+4x
96=12x
Dividing both sides by 12:
x=9612=8cm
Therefore, the value of DB is 8cm.
DB=8cm
Topper's Solved these Questions
- MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)Book:ICSEChapter:MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)Exercise:EXERCISE 24 (A)
Explore 17 Videos
- MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)Book:ICSEChapter:MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)Exercise:EXERCISE 24 (B)
Explore 10 Videos
- MATRICESBook:ICSEChapter:MATRICESExercise:Exercise 9D
Explore 25 Videos
- MIXED PRACTICE Book:ICSEChapter:MIXED PRACTICE Exercise:SET B
Explore 52 Videos
Similar Questions
In given figure, if ∠A=∠C, AB= 6 cm, BP = 15 cm, AP = 12 cm and CP= 4 cm, then find the lengths of PD and CD.

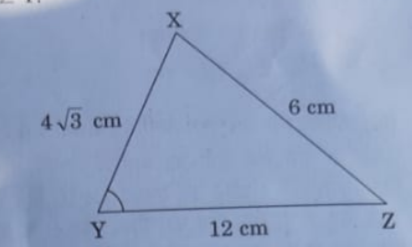
View SolutionIn figure - 3, △ABC and △XYZ are shown. if AB = 3 CM, BC = 6 cm, AC = 2√3 cm , ∠A = 80∘, ∠B = 60∘ , XY = 4√3 cm , YZ = 12 CM and XZ= 6 cm, then find the value of ∠Y
View SolutionIn figure - 3, △ABC and △XYZ are shown. if AB = 3 CM, BC = 6 cm, AC = 2√3 cm , ∠A = 80∘, ∠B = 60∘ , XY = 4√3 cm , YZ = 12 CM and XZ= 6 cm, then find the value of ∠Y

View SolutionIn the given figure, ΔABC is similar to ΔDEF,AB=(x−0.5) cm, AC=1.5xcm,DE=9cm,andDF=3xcm. Find the lengths of AB and DF.
View SolutionIf ΔABC~ΔDEF, AB=4cm, DE=6, EF=9 cm and FD=12 cm, then find the perimeter of ΔABC.
View SolutionIn the given figure, AB and DE are perpendiculars to BC. If AB = 9 cm, DE = 3 cm and AC = 24 cm, calculate AD.

View SolutionIn the given figure, if DE || BC, AE = 8 cm, EC = 2 cm and BC = 6 cm, then find DE
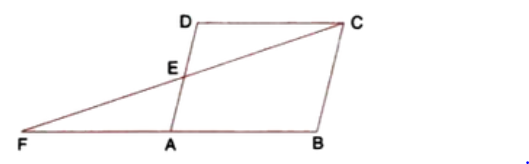
View SolutionThe given figure shows a parallelogram ABCD. E is a point in AD and CE produced meets BA produced at point F. If AE = 4 cm, AF = 8 cm and AB = 12 cm, find the perimeter of the parallelogram ABCD.
View SolutionABCD is a parallelogram where DE is perpendicular to AB. If BD= 17 cm, AE = 15 cm, and area of ΔADE=60sq. cm, find the perimeter of ABCD.

View SolutionIn the given figure, in ΔABC,DE∣∣BC so that AD= (4x - 3) cm, AE= ( 8x-7) cm, BD= (3x-1) cm and CE= (5x-3) cm . Find the value of x.
View Solution
