Column I|Column II Two intersecting circle|p. have a common tangent Two mutually external circles|q. have a common normal Two circles, one strictly inside the other|r. do not have a common tangent Two branches of a hyperbola|s. do not have a common normal
To solve the problem of matching the statements in Column I with the properties in Column II, we will analyze each case step by step.
Step 1: Analyze the first case - Two intersecting circles
- When two circles intersect, they touch at two points.
- For intersecting circles, we can draw two common tangents and one normal line connecting the centers of the circles.
- Match: Both properties P (have a common tangent) and Q (have a common normal) apply.
Step 2: Analyze the second case - Two mutually external circles
- Two mutually external circles do not touch each other.
- For these circles, we can draw four common tangents (two direct and two indirect).
- There is also a common normal line connecting the centers of the circles.
- Match: Both properties P (have a common tangent) and Q (have a common normal) apply.
Step 3: Analyze the third case - Two circles, one strictly inside the other
- When one circle is strictly inside another, they do not touch.
- Therefore, there are no common tangents between the two circles.
- However, there is a common normal line that can be drawn connecting the centers of the two circles.
- Match: Property R (do not have a common tangent) applies, and property Q (have a common normal) also applies.
Step 4: Analyze the fourth case - Two branches of a hyperbola
- The branches of a hyperbola do not touch each other.
- Similar to the previous case, there are no common tangents between the two branches.
- However, there is a normal line that can be drawn through the center of the hyperbola.
- Match: Property R (do not have a common tangent) applies, and property Q (have a common normal) also applies.
Summary of Matches:
- A (Two intersecting circles): P and Q
- B (Two mutually external circles): P and Q
- C (Two circles, one strictly inside the other): R and Q
- D (Two branches of a hyperbola): R and Q
Final Matches:
- A → P, Q
- B → P, Q
- C → R, Q
- D → R, Q
- When two circles intersect, they touch at two points.
- For intersecting circles, we can draw two common tangents and one normal line connecting the centers of the circles.
- Match: Both properties P (have a common tangent) and Q (have a common normal) apply.
- Two mutually external circles do not touch each other.
- For these circles, we can draw four common tangents (two direct and two indirect).
- There is also a common normal line connecting the centers of the circles.
- Match: Both properties P (have a common tangent) and Q (have a common normal) apply.
- When one circle is strictly inside another, they do not touch.
- Therefore, there are no common tangents between the two circles.
- However, there is a common normal line that can be drawn connecting the centers of the two circles.
- Match: Property R (do not have a common tangent) applies, and property Q (have a common normal) also applies.
- The branches of a hyperbola do not touch each other.
- Similar to the previous case, there are no common tangents between the two branches.
- However, there is a normal line that can be drawn through the center of the hyperbola.
- Match: Property R (do not have a common tangent) applies, and property Q (have a common normal) also applies.
- A (Two intersecting circles): P and Q
- B (Two mutually external circles): P and Q
- C (Two circles, one strictly inside the other): R and Q
- D (Two branches of a hyperbola): R and Q
- A → P, Q
- B → P, Q
- C → R, Q
- D → R, Q
Topper's Solved these Questions
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - All Questions
886 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Multiple correct answers type
11 Videos
Similar Questions
Knowledge Check
Two circles with radii 25 cm and 9 cm touch each other externally. Find the length of the direct common tangent.
A32 cmB50 cmC40 cmD30 cm
In figure, AB and CD are common tangents to two circles of unequal radii. Prove that AB=CD

View SolutionIn figure, AB and CD are common tangents to two circles of equal radii. Prove that AB=CD.

View SolutionIf the distance between the centres of two circles of radio 3,4 is 25 then the length of the tranverse common tangent is
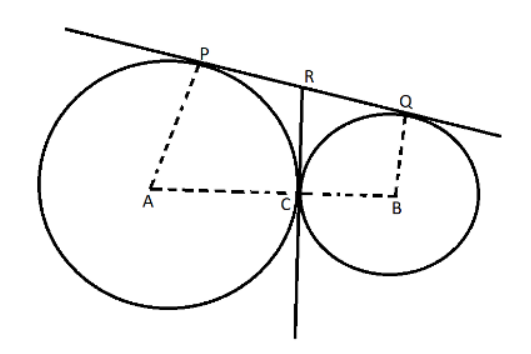
View SolutionIn Figure, two circles touch each other at the point C . Prove that the common tangent to the circles at C , bisects the common tangent at P and Q .
View Solution3 circles of radii a,b,c(a<b<c) touch each other externally and have x-axis as a common tangent then
View SolutionIn the figure, two circles touch each other at the point C.Prove that the common tangents to the circles at C, bisect the common tangents at P and Q.
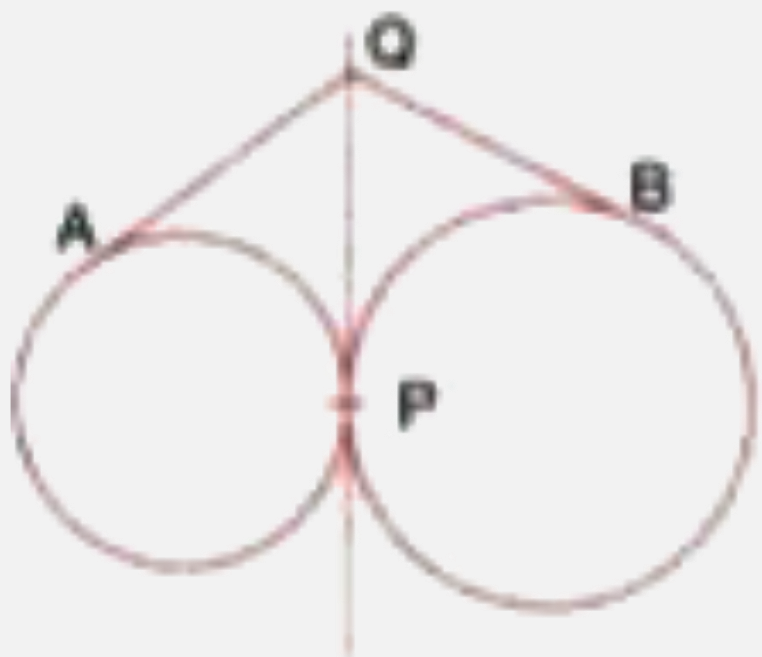
View SolutionTwo circles touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
View Solution
