Question

In what ratio does the x-axis divide the area of the region bounded by
the parabolas ${\displaystyle y=4x-x^{2}andy=x^2-x?}$

Answer

`121:4`

Explanation

Both are given curves are parabola
`y=4x-x^(2)" (1)"`
`"and "y=x^(2)-x" (2)"`
Solving (1) and (2), we get
`4x-x^(2)=x^(2)-x`
`"or "x=0, x=(5)/(2).`
Thus, two curves intersect at `O(0,0) and A((5)/(2),(15)/(4))`

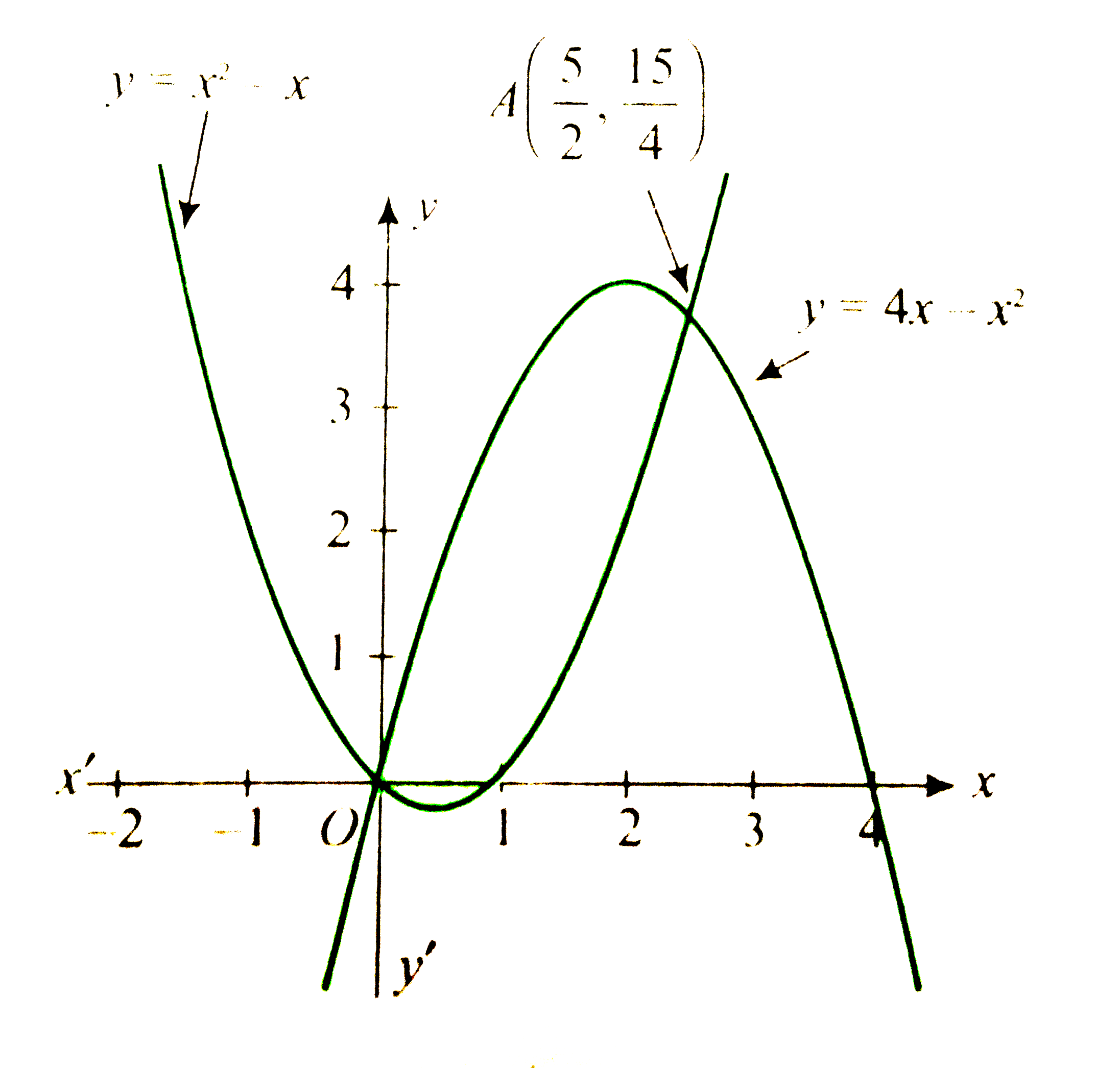
Here the area below x-axis,
`A_(1)=int_(0)^(1)(x-x^(2))dx`
`=((x^(2))/(2)-(x^(3))/(3))_(0)^(1)=(1)/(2)-(1)/(3)=(1)/(6)` sq. units
Area above x-axis,
`A_(2)=int_(0)^(5//2)(4x-x^(2))dx-int_(1)^(5//2)(x^(2)-x)dx`
`=(2x^(2)-(x^(3))/(3))_(0)^(5//2)-((x^(3))/(3)-(x^(2))/(2))_(1)^(5//2)`
`=((25)/(2)-(125)/(4))-[((125)/(4)-(25)/(8))-((1)/(3)-(1)/(2))]`
`=(25)/(2)-(125)/(2)+(25)/(8)-(1)/(6)`
`=(300-250+75-4)/(4)=(121)/(24)` sq. units.