Find the area of the region {(x,y):y2≤4x,4x2+4y2≤9}
Video Solution
Text Solution
The correct Answer is:2(9π16−98sin−1(13)+√212) sq. units
Given inequalities are
y2≤4x (1)
and 4x2+4y2≤9 (2)
Points satisfying (1) lies on or in interior to parabola y2=4x and those of (2) lies on or inside circle 4x2+4y2=9
Solving we get,
4x2+16x=9
or (2x−1)(2x+9)=0
or x=1/2 (as x=-9 not possible)
Therefore, the points of intersection of both curves are (12,√2)and(12,−√2).
The graph of these two curves and the common region of the points satisfying both the inequalities is as shown in the fiugre.
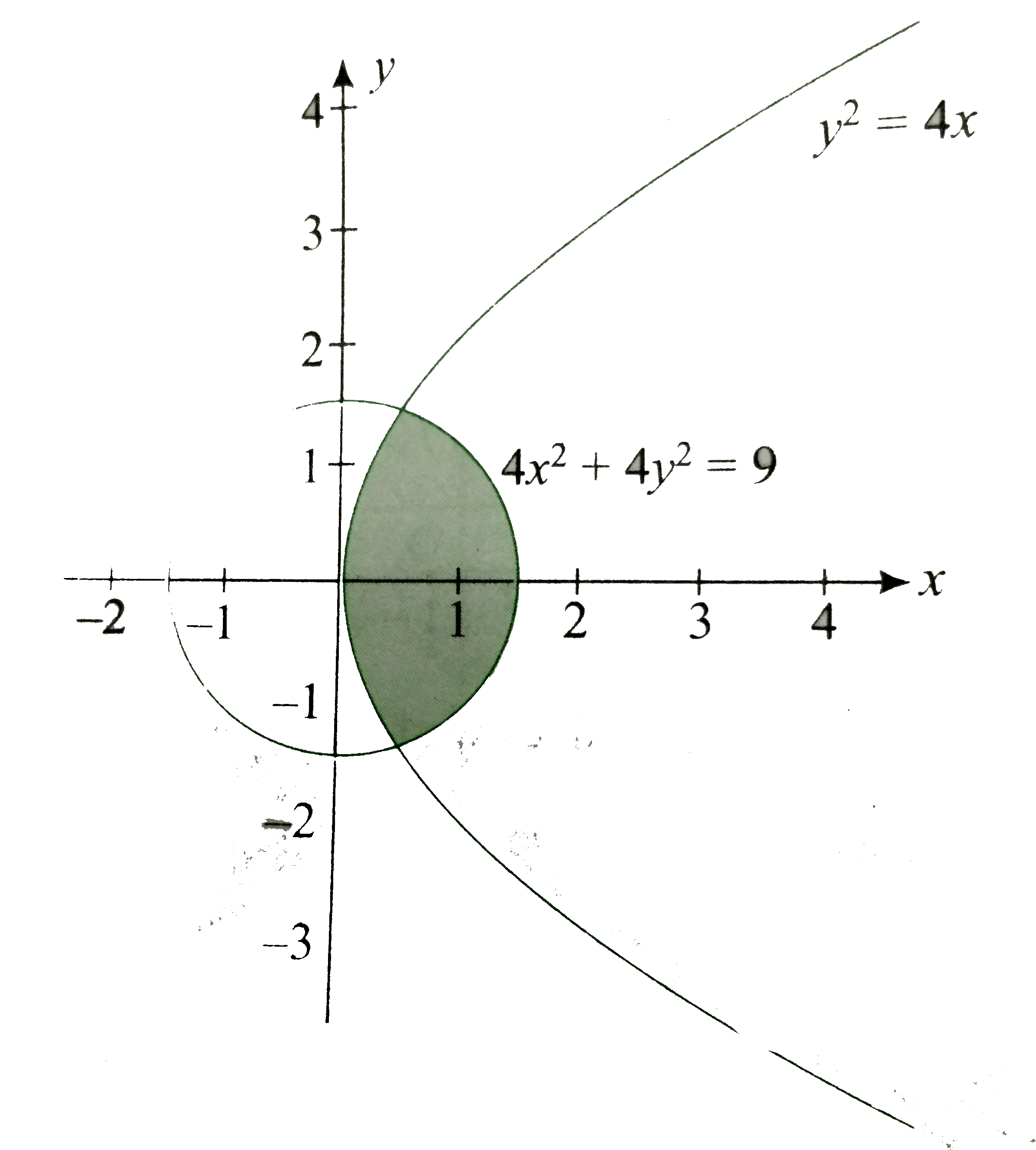
From the figure, required are is given by
A=212∫12√xdx+232∫1212√9−4x2dx
Putting 2x=t in the second integral, we get
dx=dt2
∴ A=2⎡⎢
⎢
⎢⎣12∫02√xdx+143∫1√(3)2−(t)2dt⎤⎥
⎥
⎥⎦
=2⎛⎜
⎜⎝⎡⎣2x3232⎤⎦120+14[t2√9−t2+92sin−1(t3)]31⎞⎟
⎟⎠
=2(23√2+14[{0+92sin−1(1)}−{12√8+92sin−1(13)}])
=2(9π16−98sin−1(13)+√212)
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Concept Application Exercise 9.37videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Exercises - Single Correct Answer Type40videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Concept Application Exercise 9.19videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type5videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix4videos
BINOMIAL THEOREM
Similar Questions
Find the areas of the region {(x,y):y2≤4x,4x2+4y2≤9}, using integration.
View SolutionUsing integration ,find the area of the region {(x,y):y2≤4x,4x2+4y2≤9}
View SolutionFind the area of the region {(x,y):x2≤y≤|x|}.
View SolutionFind the area of the region {(x,y) :x2+y2≤4, x+y ≥2}
View SolutionFind the area of the region {(x,y) :x2+y2≤4, x+y ≥2}
View SolutionFind the area of the region {(x,y):x2+y2≤1≤x+y}.
View SolutionUsing integration find the area of the region {(x,y):x2+y2≤2ax,y2≥ax,x,y≥0}.
View SolutionDraw a rough sketch of the region {(x,y):y2≤5x, 5x2+5y2≤36} and find the area enclosed by the region using method of integration
View SolutionFind the area of the region {(x, y):x2a2+y2b2≤1≤xa+yb}
View SolutionFind the area of the region {(x,y):x2+y2≤4,x+y≥2}, using the method of integration.
View Solution

