Sketch the region bounded by the curves $y = \sqrt{5 - x^{2}}$ and $y = | x - 1 |$ and find its area.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $\frac{5 π - 2}{4}$ sq. units

The given curves are
$y = \sqrt{5 - x^{2}} (1)$
$y = | x - 1 | (2)$
We can clearly see that on squaring the both sides of (1), equation (2) represents a circle.
But as y is + ve square root, (1) represents the upper-half of the circle with centre (0,0) and radius $\sqrt{5}$ .
Equation (2) represents the curve
$y = {\begin{matrix} - x + if x < 1 x - 1 if x \geq 1 \end{matrix}$

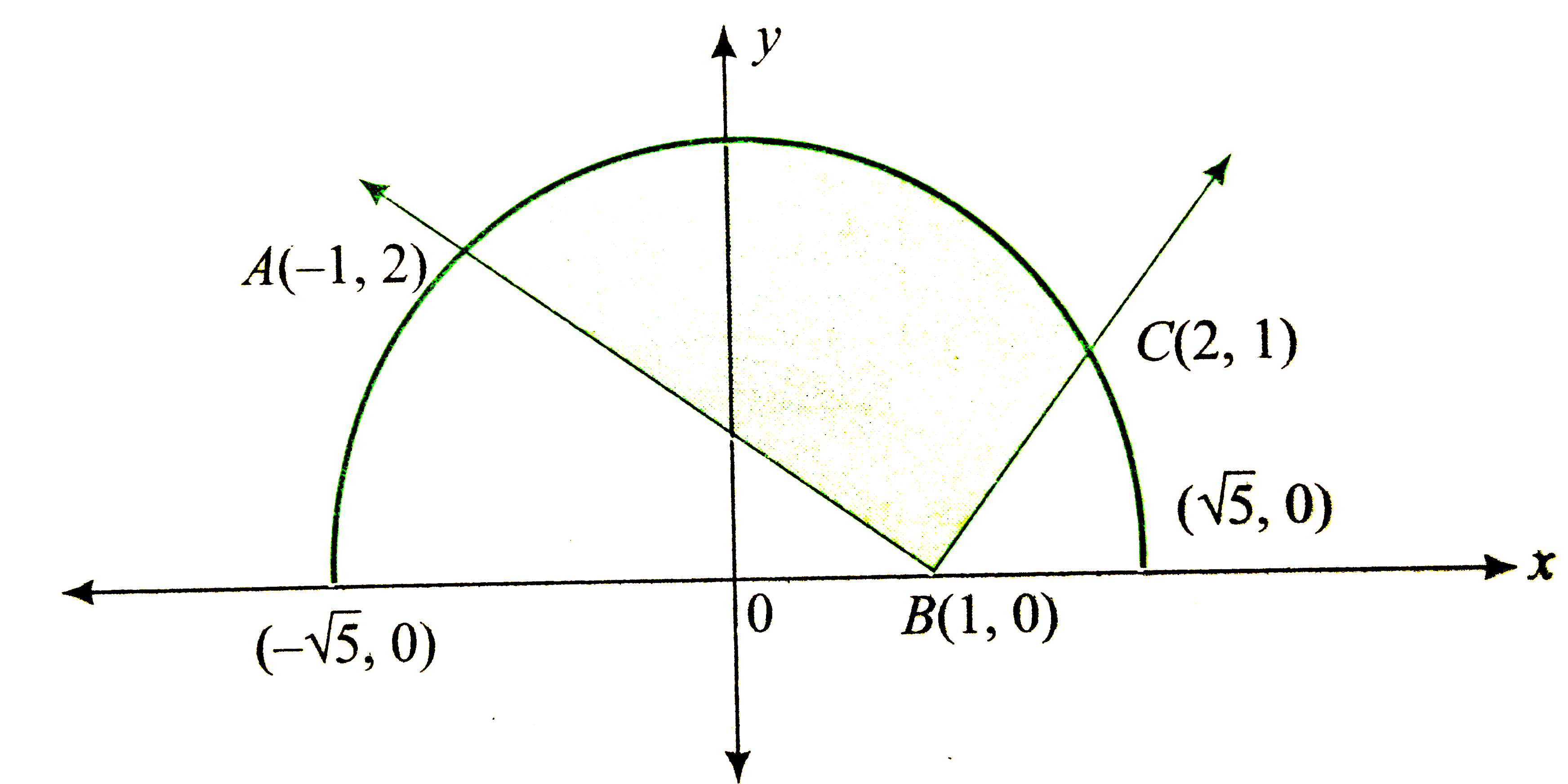
Graph of these curves are as shown in the figure with point of intersection of $y = \sqrt{5 - x^{2}} and y = - x + 1 a s A (- 1, 2)$
$and of y = \sqrt{5 - x^{2}} and y = x - 1 a s C (2, 1)$
$∴ Required area = Shaded area$
$= \int_{- 1}^{2} \sqrt{5 - x^{2}} d x - \int_{- 1}^{2} | x - 1 | d x$
$= {[\frac{x}{2} \sqrt{5 - x^{2}} + \frac{5}{2} {sin}^{- 1} (\frac{x}{\sqrt{5}})]}_{- 1}^{2} - \int_{- 1}^{1} - (x - 1) d x - \int_{1}^{2} (x - 1) d x$
$= (\frac{2}{5} \sqrt{5 - 4} + \frac{5}{2} {sin}^{- 1} \frac{2}{\sqrt{5}}) - (\frac{- 1}{2} \sqrt{5 - 1} + \frac{5}{2} {sin}^{- 1} (\frac{- 1}{\sqrt{5}})) - {(\frac{- x^{2}}{2} + x)}_{- 1}^{1} - {(\frac{x^{2}}{2} - x)}_{1}^{2}$
$= 1 + \frac{5}{2} {sin}^{- 1} \frac{2}{\sqrt{5}} + 1 + \frac{5}{2} {sin}^{- 1} (\frac{1}{\sqrt{5}})$
$- [(\frac{- 1}{2} + 1) - (\frac{- 1}{2} - 1)] - [(2 - 2) - (\frac{1}{2} - 1)]$
$= 2 + \frac{5}{2} [{sin}^{- 1} \frac{2}{\sqrt{5}} + {sin}^{- 1} \frac{1}{\sqrt{5}}] - 2 - \frac{1}{2}$
$= \frac{5}{2} [{sin}^{- 1} \frac{2}{\sqrt{5}} + {cos}^{- 1} \frac{2}{\sqrt{5}}] - \frac{1}{2} = \frac{5}{2} (\frac{π}{2}) - \frac{1}{2}$
$\frac{5 π - 2}{4}$ sq. units

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

CENGAGE ENGLISH-AREA-Concept Application Exercise 9.2

Home
Ask Doubt
Profile