Find the area bounded by y=tan−1x,y=cot−1x,andy−aξs in the first quadrant.
The correct Answer is:log√2 sq. units
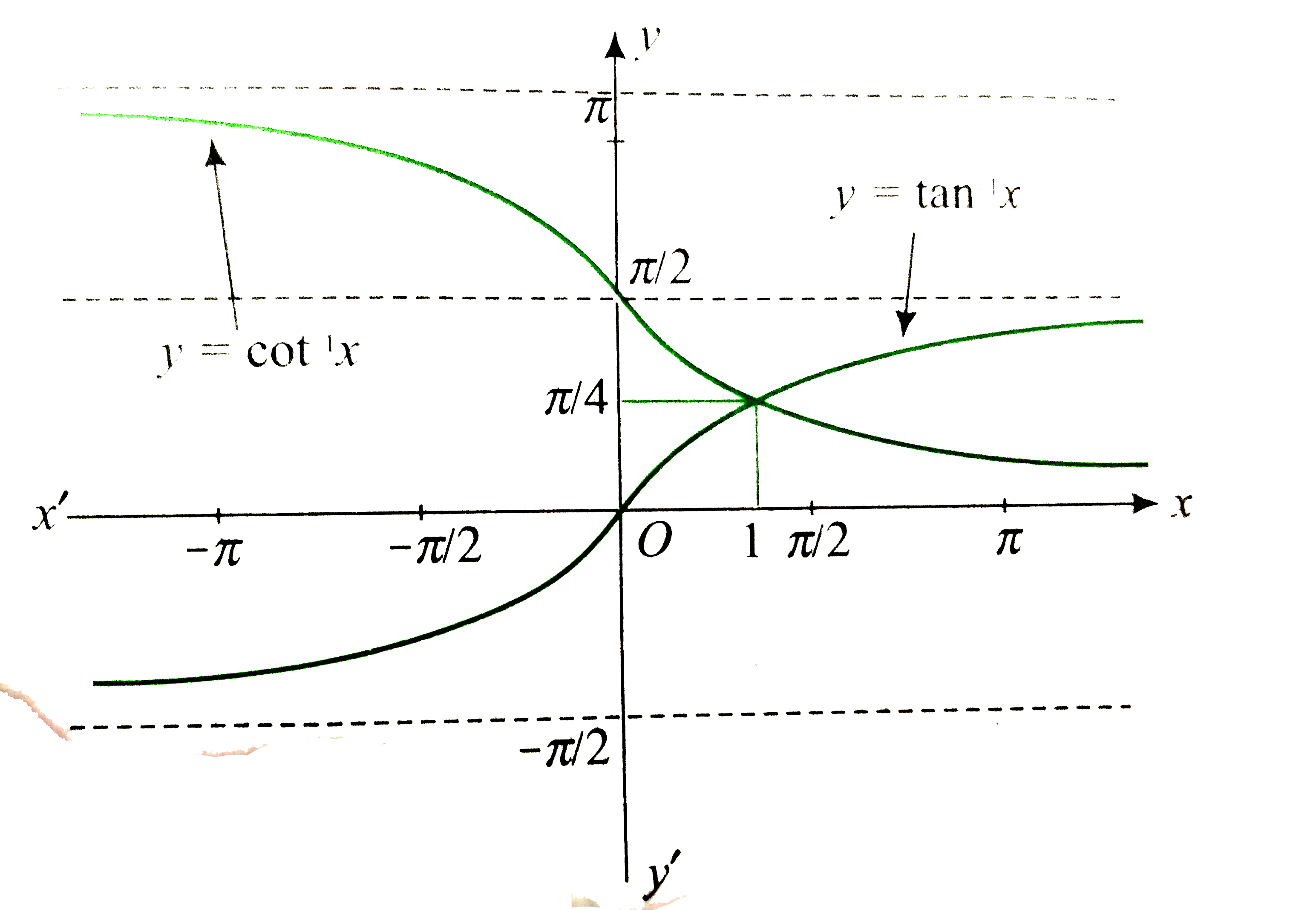
Intergrating along x-axis, we get
A=1∫0(cot−1x−tan−1x)dx=1∫0(π2−2tan−1x)dx
Intergrating a long y-axis, we get
A=2π/4∫0xdy=2.π/4∫0tanydy=[log(secy)]π/40
=log√2 sq. units
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Concept Application Exercise 9.37videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Exercises - Single Correct Answer Type40videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Concept Application Exercise 9.19videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type5videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix4videos
BINOMIAL THEOREM
Similar Questions
Find the area bounded by y=tan−1x,y=cot−1x,and y-axis in the first quadrant.
View SolutionFind the area bounded by y=sin−1x,y=cos−1x ,and the X-axis.
View SolutionFind the area bounded by y=cosx,y=x+1,y=0
View SolutionArea bounded by y=sec−1x,y=cot−1x and line x=1 is given by
View SolutionFind the area of the region bouonded by y2=4x,x=1,x=4 and x-axis in the first quadrant.
View SolutionFind the area of the region bounded by y2=4x,x=1,x=4 and the x-axis in the first quadrant.
View SolutionFind the area bounded by y2≤4x,x2+y2≥2x,andx≤y+2 in the first quadrant.
View SolutionFind the area of the region bounded by x2=16y, y=1, y=4 and the y-axis in the first quadrant.
View SolutionFind the area of the region bounded by x2=4y, y=2,y=4and the y-axis in the first quadrant.
View SolutionFind the area of the region bounded by x2=4y, y=2,y=4and the y-axis in the first quadrant.
View Solution

