A light ray gets reflected from the x=-2. If the reflected ray touches the circle x2+y2=4 and point of incident is (-2,-4), then equation of incident ray is
4y+3x+22=0
3y+4x+20=0
4y+2x+20=0
y+x+6=0
The correct Answer is:1
To find the equation of the incident ray that reflects off the line x=−2 and touches the circle given by x2+y2=4 at the point of incidence (−2,−4), we will follow these steps:
Step 1: Understand the Geometry
The incident ray strikes the line x=−2 at the point (−2,−4). The reflected ray will have a slope that can be determined using the properties of reflection.
Hint: The angle of incidence is equal to the angle of reflection.
Step 2: Find the Slope of the Reflected Ray
Since the line x=−2 is vertical, the slope of the incident ray can be denoted as m. The slope of the reflected ray will be the negative reciprocal of the slope of the incident ray.
Hint: If the slope of the incident ray is m, then the slope of the reflected ray is −1m.
Step 3: Use the Tangent Equation of the Circle
The general equation of the tangent to the circle x2+y2=4 can be expressed as:
y=mx±2√1+m2
Since the reflected ray touches the circle, we can substitute the point of tangency (−2,−4) into the tangent equation.
Hint: Substitute the coordinates of the point of tangency into the tangent equation to find m.
Step 4: Substitute the Point of Tangency
Substituting (−2,−4) into the tangent equation gives:
−4=m(−2)±2√1+m2
This simplifies to:
−4=−2m±2√1+m2
Hint: Rearrange this equation to isolate terms involving m.
Step 5: Solve for m
From the equation, we can derive:
−2m=−4±2√1+m2
This leads to two cases. Solving these will yield the possible slopes for the incident ray.
Hint: Consider both cases of the equation separately.
Step 6: Find the Slope of the Incident Ray
After solving, we find that one of the slopes is m=34. Thus, the slope of the reflected ray is −43.
Hint: Remember that the slope of the incident ray is the same as the slope you found before reflection.
Step 7: Write the Equation of the Incident Ray
Using the point-slope form of the line equation:
y−y1=m(x−x1)
Substituting m=34 and the point of incidence (−2,−4):
y+4=34(x+2)
Hint: Rearrange this equation into standard form Ax+By+C=0.
Step 8: Convert to Standard Form
Multiply through by 4 to eliminate the fraction:
4y+16=3x+6
Rearranging gives:
3x−4y+10=0
This can be rewritten as:
4y+3x+22=0
Conclusion
The equation of the incident ray is:
4y+3x+22=0
Final Hint: Check the options provided to confirm that this matches one of them.
The incident ray strikes the line x=−2 at the point (−2,−4). The reflected ray will have a slope that can be determined using the properties of reflection.
Since the line x=−2 is vertical, the slope of the incident ray can be denoted as m. The slope of the reflected ray will be the negative reciprocal of the slope of the incident ray.
The general equation of the tangent to the circle x2+y2=4 can be expressed as:
y=mx±2√1+m2
Since the reflected ray touches the circle, we can substitute the point of tangency (−2,−4) into the tangent equation.
Substituting (−2,−4) into the tangent equation gives:
−4=m(−2)±2√1+m2
This simplifies to:
−4=−2m±2√1+m2
From the equation, we can derive:
−2m=−4±2√1+m2
This leads to two cases. Solving these will yield the possible slopes for the incident ray.
After solving, we find that one of the slopes is m=34. Thus, the slope of the reflected ray is −43.
Using the point-slope form of the line equation:
y−y1=m(x−x1)
Substituting m=34 and the point of incidence (−2,−4):
y+4=34(x+2)
Multiply through by 4 to eliminate the fraction:
4y+16=3x+6
Rearranging gives:
3x−4y+10=0
This can be rewritten as:
4y+3x+22=0
The equation of the incident ray is:
4y+3x+22=0
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Multiple Correct Anser Type
29 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Linked Comprehension Type (For Problem 1-3)
3 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.20
1 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
- CIRCLESBOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
Statement I A ray of light incident at the point (-3,-1) gets reflected from the tangent at (0,-1) to the circle x2+y2=1. If the reflected ray touches the circle, then equation of the reflected ray is 4y-3x=5
Statement II The angle of incidence = angle of reflection i.e. ∠i=∠r,
View SolutionA ray of light incident at the point (-2, -1) gets reflected from the tangent at (0, -1) to the circle x2+y2=1. The reflected ray touches the circle. The equation of the line along which the incident ray moved is
View SolutionA ray of light is sent through the point P(1,2,3) and is reflected on the XY plane. If the reflected ray passes through the point Q(3,2,5) then the equation of the reflected ray is
View SolutionA ray of light is sent along the line which passes through the point (2, 3). The ray is reflected from the point P on x-axis. If the reflected ray passes through the point (6, 4), then the co-ordinates of P are
View SolutionIf an incident ray passes through the focus, the reflected ray will
View SolutionDraw a diagram showing the reflection of a light ray from a plane mirror. Label on it the incident ray, the reflected ray, the normal, the angle of incidence i and the angle of reflection r.
View SolutionA ray of light travelling along the line OA (O being origin ) is reflected by the line mirror x−y+1=0 is the point of incidence being A (1,2) the reflected ray , travelling along AB is again reflected by the line mirror x−y=2, the point of incidence being B. If this reflected ray moves along BC, find the equation of the lne BC.
View SolutionThe diagram below shows a light ray striking and reflecting from a plane mirror AO is the incident ray and OB the reflected ray. The angle between the incident ray and the reflected ray is 120∘.
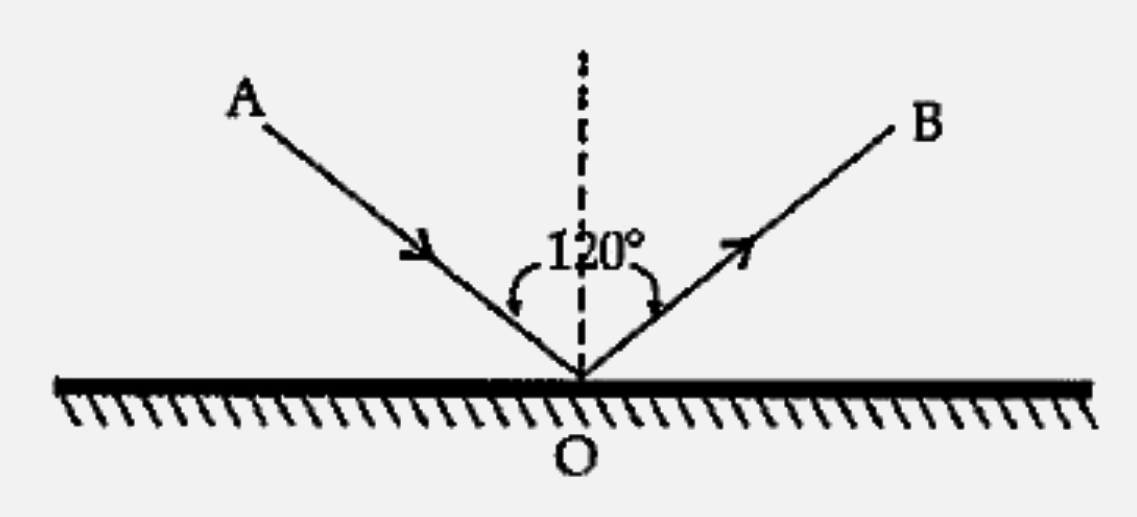
What is the value of the angle of reflection?
View SolutionA ray is incident on a plane mirro. Its reflected ray is perpendicular to the incident ray. Find the angle of incidence.
View SolutionThe diagram below shows a light ray striking and reflecting from a plane mirror AO is the incident ray and OB the reflected ray. The angle between the incident ray and the reflected ray is 120∘.

If two plane mirrors are used and kept facing parallel to each other, how many images are formed if the object is kept in between them?
View Solution
