The greatest and the least value of the function, f(x)=√1−2x+x2−√1+2x+x2,x∈(−∞,∞) are
A
8
B
7
C
6
D
4
Video Solution
Text Solution
The correct Answer is:2
y=√9−a2+2ax−x2
y=√16−x2
⇒y2+(x−a)2=9
⇒y2+x2=16
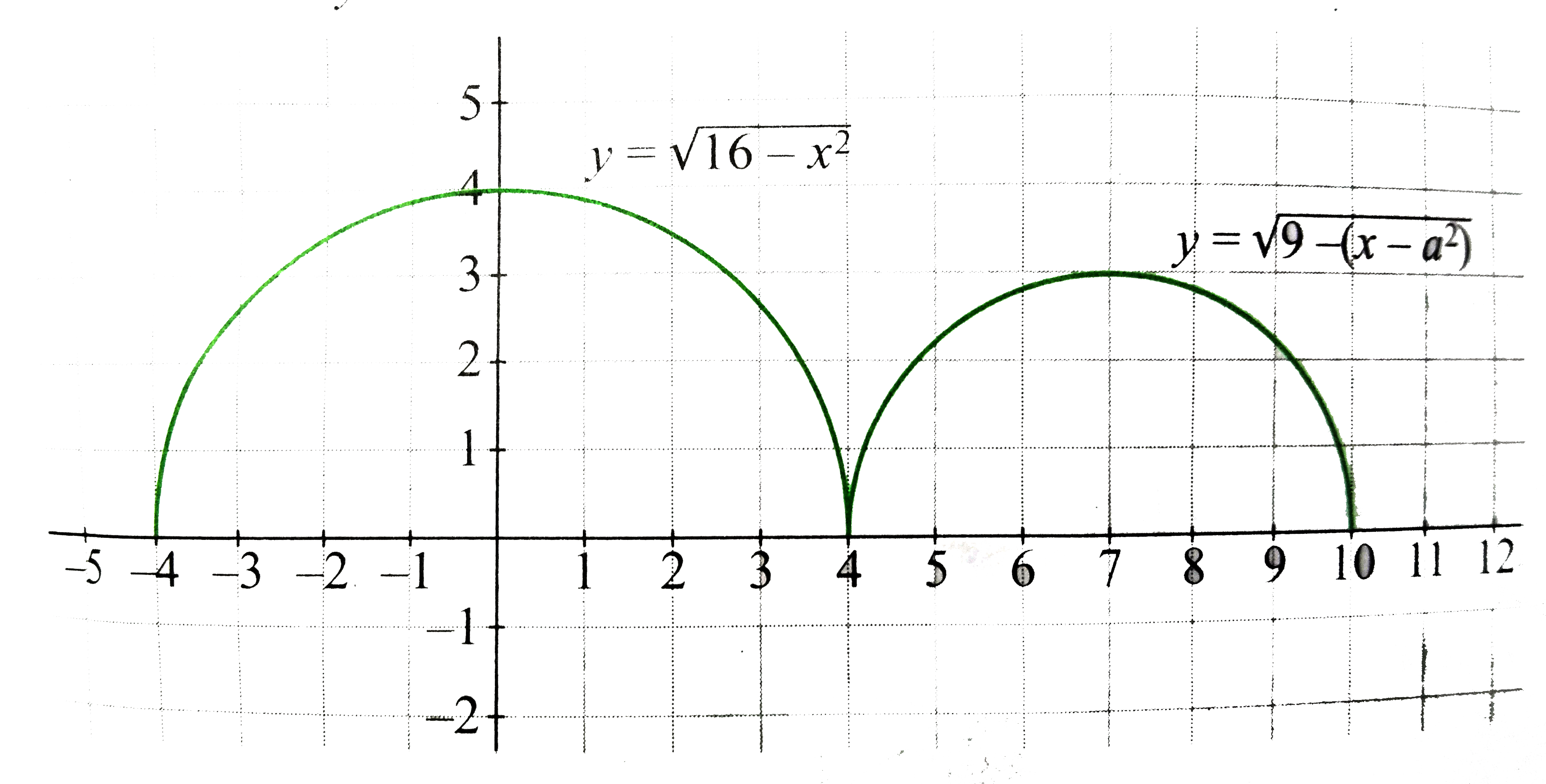
If a>7 , no solution exist, So, a≤7
Hence, maximum value of a is 7.
|
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Multiple Correct Anser Type
29 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Linked Comprehension Type (For Problem 1-3)
3 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.20
1 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
- CIRCLESBOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
The greatest, the least values of the function ,f(x)=2−√1+2x+x2,x∈[−2,1] are respectively
View SolutionThe range of the function f(x)=√2−x+√1+x
View SolutionThe domain of the function f(x)=√x−√1−x2 is
View SolutionThe function f(x)=1+xln(x+√1+x2)−√1−x2 is:
View SolutionDifference between the greatest and the least values of the function f(x)=x(lnx−2) on [1,e2] is
View SolutionFind the domain of the following functions: f(x)=√x−2x+2+√1−x1+x
View SolutionThe domain of definition of the function f(x)=√x−2x+2+√1−x1+x is a.(−∞,−2]∪[2,∞) b. [−1,1] c. φ d. none of these
View SolutionThe greatest value of the fucntion f(x)=sin−1x2 in interval [−1/√2,1/√2] is
View Solutionlimx→∞x{√x2+1−√x2−1)}
View SolutionThe function f(x)=max{(1−x),(1+x),2},x∈(−∞,∞) is
View Solution
