Let A(p2,−p),B(q2,q),C(r2,−r) be the vertices of triangle ABC. A parallelogram AFDE is drawn with D,E, and F on the line segments BC, CA and AB, respectively. Using calculus, show that the maximum area of such a parallelogram is 12(p+q)(q+r)(p−r).

From similar triangle s FBD and ABC , c−xc=yb
or y=(b/c)c−x
∴ Z=Area of AFDE= xysinA=bsinAc(cx−x2)
0<x<c
∴dzdx=bsinAc(c−2x)=0prx=c/2
d2Z(dx2)x=c/2=−2cbsinA<0
Thus Z has maxima at x=c2.So the greatest area of parallelogram AFDE is
(bc)msinA(c2/a)=12(12bcsinA)
=12△ABC=(12)×∣∣
∣
∣∣∣∣
∣
∣∣p2−p=1q2q=1r2−r=1∣∣
∣
∣∣∣∣
∣
∣∣
=14∣∣
∣
∣∣∣∣
∣
∣∣p2−p=1q2−p2q+p=0r2−p2−r+p=1∣∣
∣
∣∣∣∣
∣
∣∣R2→R2−R1<br>R3→R3−R1
=14|(q+p)(q+r)(p−r)|
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Concept Application Exercise 6.110videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Concept Application Exercise 6.210videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Matrix Match Type14videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - Single Correct Answer Type46videos
METHODS OF DIFFERENTIATION
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type6videos
MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONS
Similar Questions
P,Q,R are the points on the sides AB, BC and CA respectively of triangle ABC such that AP:PB=BQ:QC=AR:RC=1:2. Show that PBQR is a parallelogram.
View SolutionThe diagonals of a parallelogram ABCD intersect at a point O. Through O, a line is drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.
View SolutionProve that the figure formed by joining the mid-points of the pair of consecutive sides of a quadrilateral is a parallelogram. OR ABCD is a parallelogram in which P,Q,R and S are mid-points of the sides AB,BC,CD and DA respectively. AC is a diagonal. Show that : PQ∣∣AC and PQ=12AC SR∣∣AC and SR=12AC PQ=SR (iv) PQRS is a parallelogram.
View SolutionP and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar (APB) = ar (BQC).
View SolutionLet P be an interior point of a triangle ABC , Let Q and R be the reflections of P in AB and AC , respectively if Q .A , R are collinear then ∠A equals -
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
View SolutionIn ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.
View SolutionIf P(2, 4), Q(0, 3), R(3, 6) and S(5, y) are the vertices of a parallelogram PQRS , then the value of y is (a) 7 (b) 5 (c) -7 (d) -8
View SolutionABCD is a parallelogram. P is the mid-point of AB.BD and CP intersect at Q such that CQ:QP=3:1. If ar (PBQ)=10 cm2, find the area of parallelogram ABCD
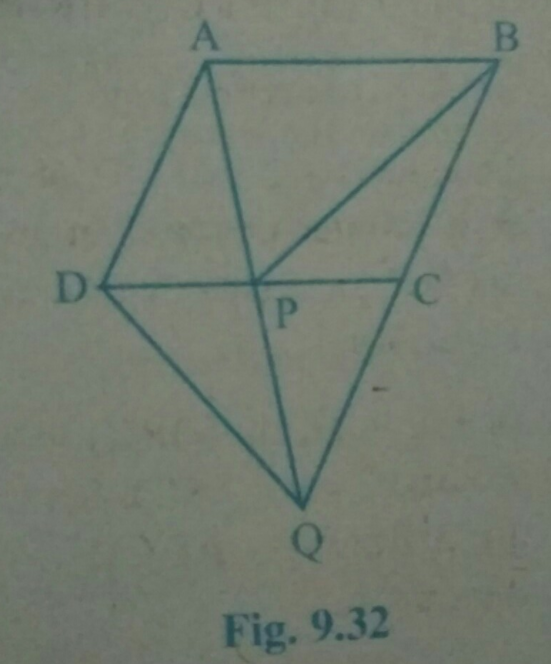
View SolutionIn Fig. 9.32, ABCD is a parallelogram and BC is produced to a point Q such thatAD = CQ. If AQ intersect DC at P, show that ar (BPC) = ar (DPQ).
 View Solution
View Solution

