In a right triangle ABC, right angled at C, P is the mid-point of hypotenuse AB. C is joined to P and produced to a point D, such that DP = CP. Point D is joined to point B. Show that:
Angle DBC is a right angle.
To prove that angle DBC is a right angle in triangle ABC, where C is the right angle, we can follow these steps:
1. Draw Triangle ABC:
- Start by drawing triangle ABC with the right angle at C. Let A and B be the other two vertices.
2. Identify Midpoint P:
- Mark point P as the midpoint of hypotenuse AB. This means AP = PB.
3. Join C to P and Extend to D:
- Draw line segment CP and extend it to point D such that DP = CP.
4. Join D to B:
- Draw line segment DB.
5. Establish Triangle Congruence:
- In triangles APC and DPB, we have:
- AP = PB (since P is the midpoint of AB)
- CP = DP (given)
- Angle APC = Angle DPB (vertically opposite angles)
- Therefore, by the Side-Angle-Side (SAS) congruence criterion, triangle APC is congruent to triangle DPB.
6. Corresponding Angles:
- From the congruence of triangles APC and DPB, we can conclude that angle PAC = angle DBP (corresponding parts of congruent triangles).
7. Identify Parallel Lines:
- Since angle PAC = angle DBP, and they are alternate interior angles formed by the transversal AB, we can conclude that lines AC and BD are parallel.
8. Adjacent Angles:
- Angles ACB and DBC are adjacent angles formed between the parallel lines AC and BD.
9. Sum of Angles:
- The sum of adjacent angles formed by a transversal with two parallel lines is 180 degrees:
- Angle ACB + Angle DBC = 180 degrees.
10. Substituting Known Values:
- We know angle ACB = 90 degrees (since triangle ABC is right-angled at C).
- Therefore, we can substitute:
- 90 degrees + Angle DBC = 180 degrees.
11. Solve for Angle DBC:
- Rearranging gives us:
- Angle DBC = 180 degrees - 90 degrees = 90 degrees.
12. Conclusion:
- Hence, we have shown that angle DBC is a right angle.
- Start by drawing triangle ABC with the right angle at C. Let A and B be the other two vertices.
- Mark point P as the midpoint of hypotenuse AB. This means AP = PB.
- Draw line segment CP and extend it to point D such that DP = CP.
- Draw line segment DB.
- In triangles APC and DPB, we have:
- AP = PB (since P is the midpoint of AB)
- CP = DP (given)
- Angle APC = Angle DPB (vertically opposite angles)
- Therefore, by the Side-Angle-Side (SAS) congruence criterion, triangle APC is congruent to triangle DPB.
- From the congruence of triangles APC and DPB, we can conclude that angle PAC = angle DBP (corresponding parts of congruent triangles).
- Since angle PAC = angle DBP, and they are alternate interior angles formed by the transversal AB, we can conclude that lines AC and BD are parallel.
- Angles ACB and DBC are adjacent angles formed between the parallel lines AC and BD.
- The sum of adjacent angles formed by a transversal with two parallel lines is 180 degrees:
- Angle ACB + Angle DBC = 180 degrees.
- We know angle ACB = 90 degrees (since triangle ABC is right-angled at C).
- Therefore, we can substitute:
- 90 degrees + Angle DBC = 180 degrees.
- Rearranging gives us:
- Angle DBC = 180 degrees - 90 degrees = 90 degrees.
- Hence, we have shown that angle DBC is a right angle.
Topper's Solved these Questions
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - ISOSCELES TRIANGLES
2 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - INEQUALITIES
7 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - LOGARITHM
9 Videos
- CHAPTERWISE REVISION (STAGE 1) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 1) EXERCISE - Graphical solution
10 Videos
- CIRCLEBOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(D)
12 Videos
Similar Questions
In a right triangle ABC, right angled at C, P is the mid-point of hypotenuse AB. C is joined to P and produced to a point D, such that DP = CP. Point D is joined to point B. Show that:
ΔDBC≅ΔACB
View SolutionIn a right triangle ABC, right angled at C, P is the mid-point of hypotenuse AB. C is joined to P and produced to a point D, such that DP = CP. Point D is joined to point B. Show that:
CP=12AB
View SolutionIn a right triangle ABC, right angled at C, P is the mid-point of hypotenuse AB. C is joined to P and produced to a point D, such that DP = CP. Point D is joined to point B. Show that:
ΔAPC≅ΔBPD
View SolutionIn right triangle ABC, right angle at C, M is the mid-point of the hydrotenuse AB. C is joined to M and produced to a point D such that DM=CM. Point D is joined to point B. Show that
(i) ΔAMC≅ΔBMD (ii) ∠DBC=∠ACB
(iii) ΔDBC≅ΔACB (iv) CM=12AB
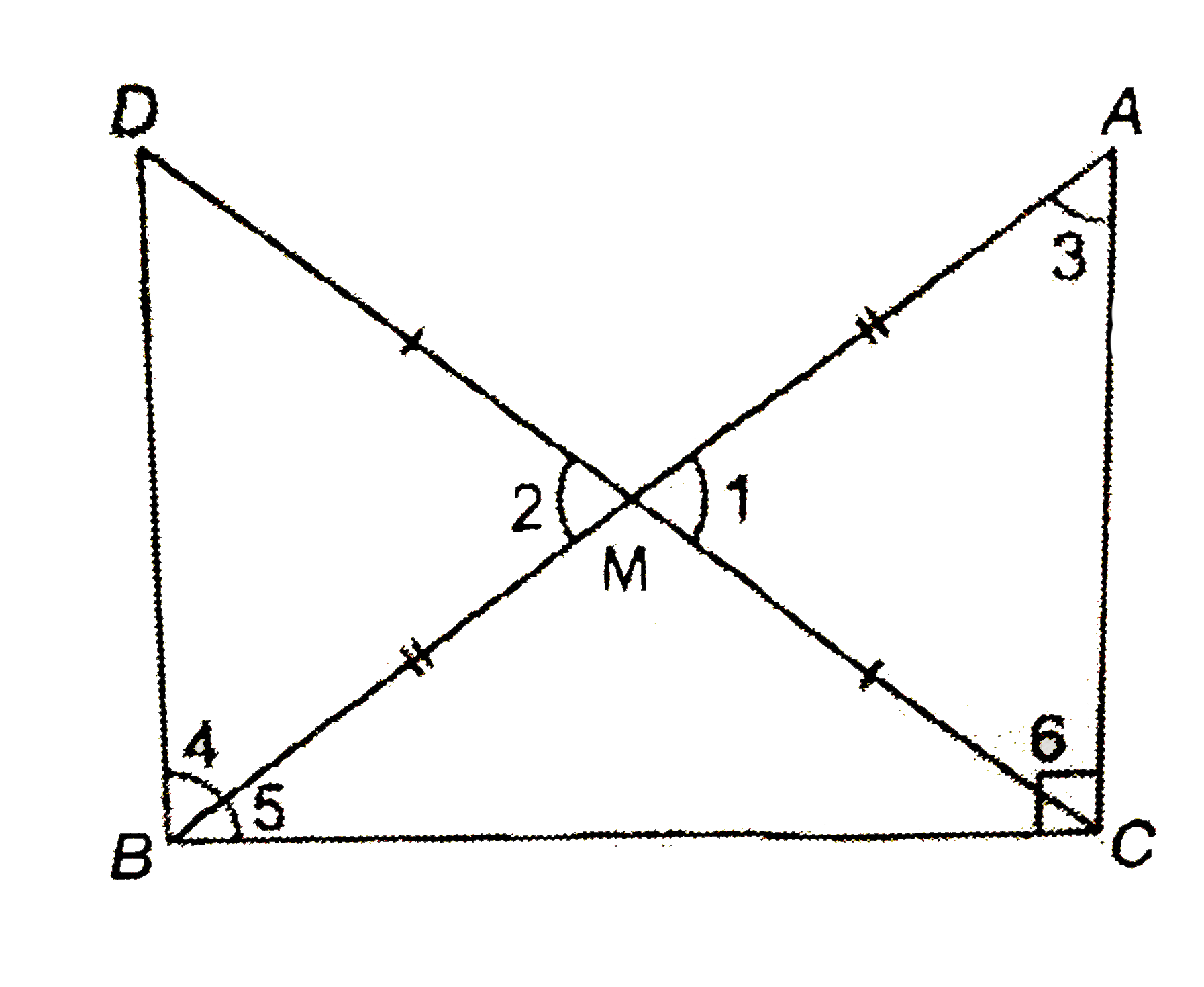
View SolutionIn right triangle ABC, right-angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see Fig. 7.23). Show that:
(i) ΔAMC≅ΔBMD
(ii) ∠DBC is a right angle
(iii) ΔDBC≅ΔACB
(iv) CM=12AB

View SolutionIn right triangle ABC , right angle at C, M is the mid-point of the hypotenuse AB. C is jointed to M and produced to a point D such that DM=CM. Point D is joined to point B. Show that AMC≅BMD (ii) ∠DBC=∠ACB DBC≅ACB (iii) CM=12AB
View SolutionABC is a triangle right angled at C and M is mid-point of hypotenuse AB. Line drawn through M and parallel to BC intersects AC at D. Show that:
MD is mid-point of AC.
View SolutionIn a right ABC right-angled at C , if D is the mid-point of BC , prove that BC2=4 (AD2−AC2) .
View SolutionIn Fig. 3, ABC is a right triangle, right angled at C and D is the mid-point of BC. Prove that AB2=4AD2−3AC2.
View SolutionIf D is the mid-point of the hypotenuse AC of a right triangle ABC, prove that BD=12AC
View Solution
