In a right triangle ABC, right angled at C, P is the mid-point of hypotenuse AB. C is joined to P and produced to a point D, such that DP = CP. Point D is joined to point B. Show that:
ΔDBC≅ΔACB
To show that triangle DBC is congruent to triangle ACB, we will use the properties of congruent triangles and the information provided in the problem.
1. Identify the Given Information:
- Triangle ABC is a right triangle with a right angle at C.
- P is the midpoint of hypotenuse AB.
- CP = DP (D is produced from P such that DP = CP).
- We need to show that triangle DBC is congruent to triangle ACB.
2. Consider Triangle ABC and Triangle PDB:
- Since P is the midpoint of AB, we have:
AB=PB
- Angle ABC is equal to angle DPB because they are vertically opposite angles:
∠ABC=∠DPB
- From the problem, we know:
CP=PD
3. Apply the Side-Angle-Side (SAS) Congruence Criterion:
- From the above information, we have:
- AB=PB (1)
- ∠ABC=∠DPB (2)
- CP=PD (3)
- Therefore, by the SAS criterion, triangle ABC is congruent to triangle PDB:
△ABC≅△PDB
4. Extract Corresponding Parts from the Congruent Triangles:
- From the congruence of triangles ABC and PDB, we know:
- AC=DB (corresponding sides)
- ∠CAP=∠BDP (corresponding angles)
5. Consider Triangle ACB and Triangle CDB:
- Now, we will compare triangle ACB and triangle CDB.
- We know:
- AC=DB (from the previous step)
- ∠CAP=∠BDP (from the previous step)
- CB is a common side for both triangles.
6. Apply the SAS Congruence Criterion Again:
- Therefore, by the SAS criterion, triangle ACB is congruent to triangle DBC:
△ACB≅△DBC
Conclusion:
Thus, we have shown that triangle DBC is congruent to triangle ACB.
- Triangle ABC is a right triangle with a right angle at C.
- P is the midpoint of hypotenuse AB.
- CP = DP (D is produced from P such that DP = CP).
- We need to show that triangle DBC is congruent to triangle ACB.
- Since P is the midpoint of AB, we have:
AB=PB
- Angle ABC is equal to angle DPB because they are vertically opposite angles:
∠ABC=∠DPB
- From the problem, we know:
CP=PD
- From the above information, we have:
- AB=PB (1)
- ∠ABC=∠DPB (2)
- CP=PD (3)
- Therefore, by the SAS criterion, triangle ABC is congruent to triangle PDB:
△ABC≅△PDB
- From the congruence of triangles ABC and PDB, we know:
- AC=DB (corresponding sides)
- ∠CAP=∠BDP (corresponding angles)
- Now, we will compare triangle ACB and triangle CDB.
- We know:
- AC=DB (from the previous step)
- ∠CAP=∠BDP (from the previous step)
- CB is a common side for both triangles.
- Therefore, by the SAS criterion, triangle ACB is congruent to triangle DBC:
△ACB≅△DBC
Thus, we have shown that triangle DBC is congruent to triangle ACB.
Topper's Solved these Questions
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - ISOSCELES TRIANGLES
2 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - INEQUALITIES
7 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - LOGARITHM
9 Videos
- CHAPTERWISE REVISION (STAGE 1) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 1) EXERCISE - Graphical solution
10 Videos
- CIRCLEBOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(D)
12 Videos
Similar Questions
In a right triangle ABC, right angled at C, P is the mid-point of hypotenuse AB. C is joined to P and produced to a point D, such that DP = CP. Point D is joined to point B. Show that:
ΔAPC≅ΔBPD
View SolutionIn a right triangle ABC, right angled at C, P is the mid-point of hypotenuse AB. C is joined to P and produced to a point D, such that DP = CP. Point D is joined to point B. Show that:
CP=12AB
View SolutionIn a right triangle ABC, right angled at C, P is the mid-point of hypotenuse AB. C is joined to P and produced to a point D, such that DP = CP. Point D is joined to point B. Show that:
Angle DBC is a right angle.
View SolutionIn right triangle ABC, right angle at C, M is the mid-point of the hydrotenuse AB. C is joined to M and produced to a point D such that DM=CM. Point D is joined to point B. Show that
(i) ΔAMC≅ΔBMD (ii) ∠DBC=∠ACB
(iii) ΔDBC≅ΔACB (iv) CM=12AB
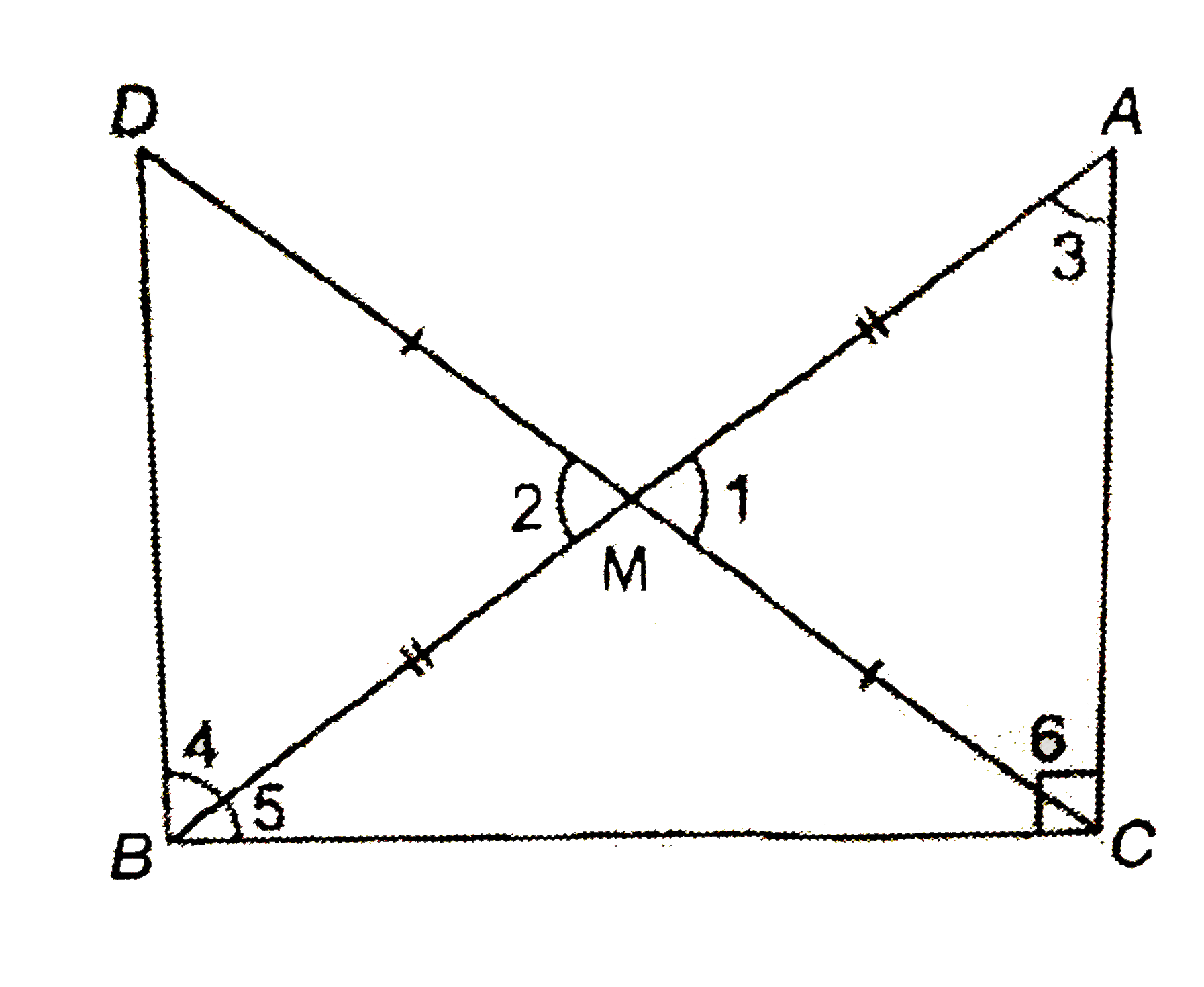
View SolutionIn right triangle ABC, right-angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see Fig. 7.23). Show that:
(i) ΔAMC≅ΔBMD
(ii) ∠DBC is a right angle
(iii) ΔDBC≅ΔACB
(iv) CM=12AB

View SolutionIn right triangle ABC , right angle at C, M is the mid-point of the hypotenuse AB. C is jointed to M and produced to a point D such that DM=CM. Point D is joined to point B. Show that AMC≅BMD (ii) ∠DBC=∠ACB DBC≅ACB (iii) CM=12AB
View SolutionABC is a triangle right angled at C and M is mid-point of hypotenuse AB. Line drawn through M and parallel to BC intersects AC at D. Show that:
MD is mid-point of AC.
View SolutionIn Fig. 3, ABC is a right triangle, right angled at C and D is the mid-point of BC. Prove that AB2=4AD2−3AC2.
View SolutionIf D is the mid-point of the hypotenuse AC of a right triangle ABC, prove that BD=12AC
View SolutionIn a right-angled triangle ABC,∠ABC=90∘ and D is mid-point of AC. Prove that BD=12AC.
View Solution
