Question

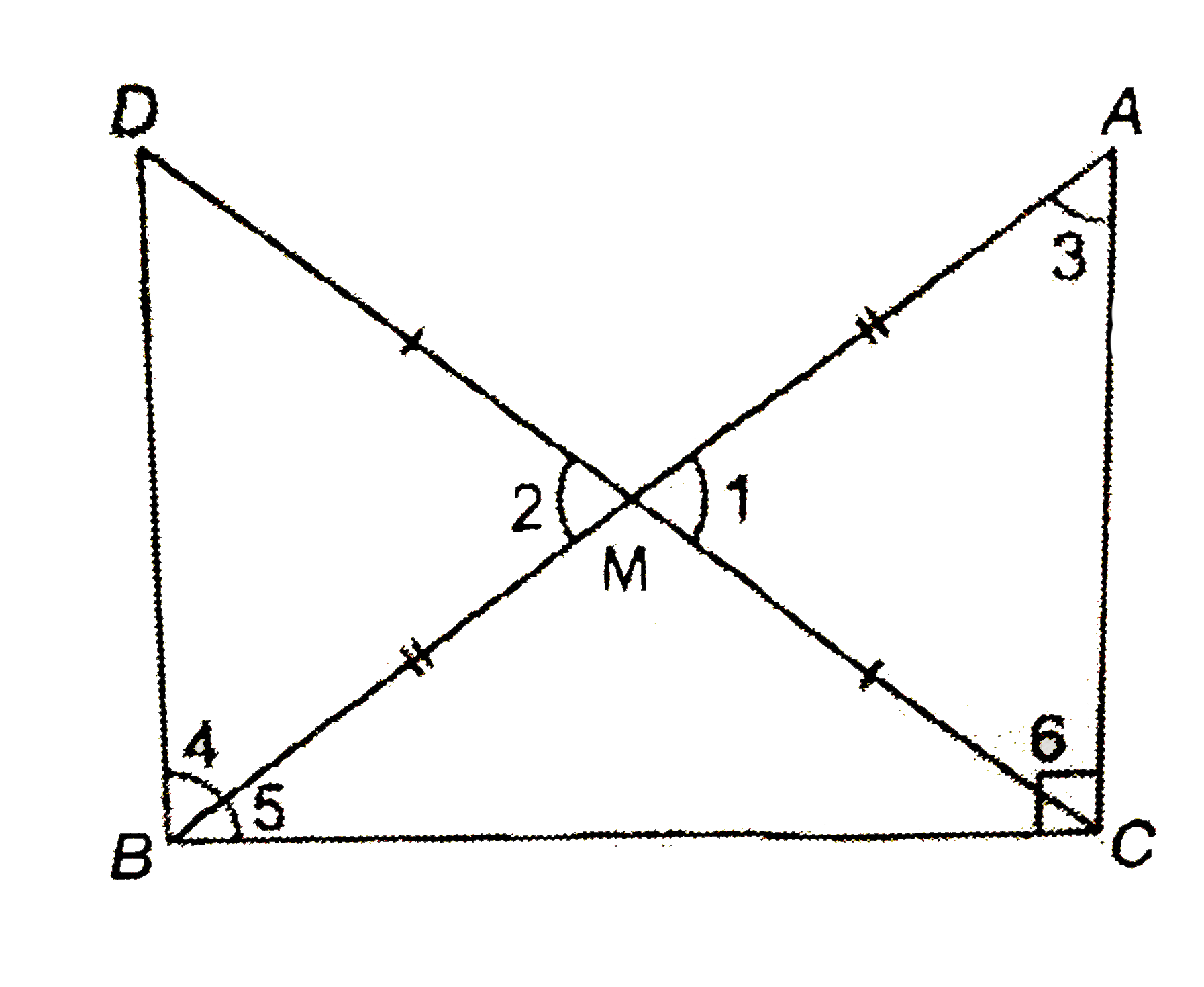
In a right triangle ABC, right angled at C, P is the mid-point of hypotenuse AB. C is joined to P and produced to a point D, such that DP = CP. Point D is joined to point B. Show that:
$CP=\frac{1}{2}AB$

Explanation

To solve the problem, we need to show that in triangle ABC, right-angled at C, with P as the midpoint of hypotenuse AB, and point D such that DP = CP, it follows that CP = (1/2)AB.

1. Identify the Triangle and Points:
Let triangle ABC be a right triangle with the right angle at C. Let P be the midpoint of the hypotenuse AB.

2. Establish the Lengths:
Since P is the midpoint of AB, we have:
\( AP = PB = \frac{1}{2} AB \)

3. Join Points:
Join point C to point P, and extend it to point D such that \( DP = CP \). This means that D is located such that the length of segment DP is equal to the length of segment CP.

4. Use Congruent Triangles:
In triangles APC and BPD:
- \( AP = BP \) (since P is the midpoint of AB)
- \( DP = CP \) (given)
- \( \angle APC = \angle BPD \) (by vertical angles)

By the Side-Side-Angle (SSA) congruence criterion, we can conclude that:
\( \triangle APC \cong \triangle BPD \)

5. Corresponding Parts of Congruent Triangles:
From the congruence of triangles APC and BPD, we have:
\( AC = BD \)

6. Establish Parallel Lines:
Since \( AC \) is equal to \( BD \) and the angles \( \angle ACP \) and \( \angle DBP \) are equal (corresponding angles), we can conclude that:
\( AC \parallel BD \)

7. Use the Angle Sum Property:
Since \( AC \parallel BD \), the angles \( \angle ACB + \angle DBC = 180^\circ \). Given that \( \angle ACB = 90^\circ \) (as triangle ABC is right-angled), we have:
\( 90^\circ + \angle DBC = 180^\circ \implies \angle DBC = 90^\circ \)

8. Establish Congruence of Triangles ACB and DBC:
Now, in triangles ACB and DBC:
- \( AC = BD \) (from earlier)
- \( \angle ACB = \angle DBC = 90^\circ \)
- \( CB = CB \) (common side)

Therefore, by the Side-Angle-Side (SAS) congruence criterion:
\( \triangle ACB \cong \triangle DBC \)

9. Conclude the Lengths:
From the congruence of triangles ACB and DBC, we have:
\( AB = DC \)
Since P is the midpoint of AB, we can express:
\( CP = \frac{1}{2} AB \)

10. Final Conclusion:
Thus, we have shown that:
\( CP = \frac{1}{2} AB \)
Hence, it is proved.