In each of the figures [4.222 (i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segments are marked. Find the value of x in each of the following: (FIGURE)
To solve the problem of finding the value of x in the given triangles with a line segment drawn parallel to one side, we will use the Basic Proportionality Theorem (also known as Thales' theorem). This theorem states that if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally.
1. Identify the Triangle and the Parallel Line Segment:
Let's denote the triangle as ABC with the line segment DE drawn parallel to side BC. The lengths of the segments are given as AD=a, DB=b, DE=c, and EC=x.
2. Apply the Basic Proportionality Theorem:
According to the theorem, the ratios of the segments created by the parallel line are equal. Therefore, we can write:
ADDB=DEEC
Substituting the known values:
ab=cx
3. Cross-Multiply to Solve for x:
Cross-multiplying gives us:
a⋅x=b⋅c
Now, to isolate x, we divide both sides by a:
x=b⋅ca
4. Conclusion:
Thus, the value of x is given by the formula:
x=b⋅ca
Let's denote the triangle as ABC with the line segment DE drawn parallel to side BC. The lengths of the segments are given as AD=a, DB=b, DE=c, and EC=x.
According to the theorem, the ratios of the segments created by the parallel line are equal. Therefore, we can write:
ADDB=DEEC
Substituting the known values:
ab=cx
Cross-multiplying gives us:
a⋅x=b⋅c
Now, to isolate x, we divide both sides by a:
x=b⋅ca
Thus, the value of x is given by the formula:
x=b⋅ca
Topper's Solved these Questions
Similar Questions
Knowledge Check

In the figure above, if line segment AB is parallel to line segment CD, what is the value of y?A12B15C18D20
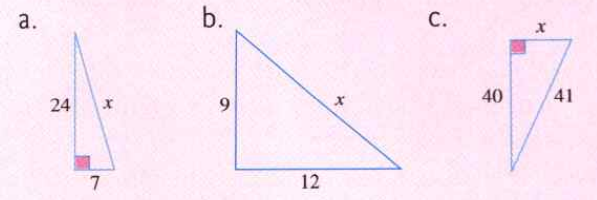
In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle. The length of different line-segments are marked in each figure. Determine x, y, z in each case.
View SolutionIn each of the figures given below. Find x and y
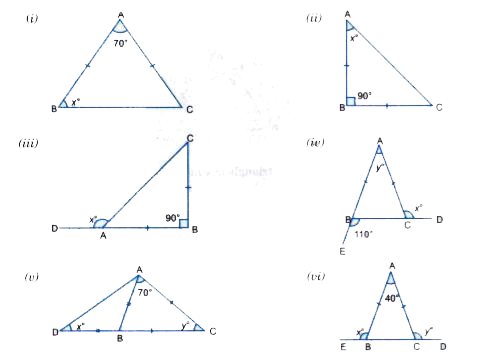
View SolutionFind the unknown angles marked in each of the following figures :

View SolutionDraw a line segment AB and bisect it. Bisect one of the equal parts to obtain a line segment of length 14(AB)
View SolutionFind the unknown marked angles in each of the following figures :
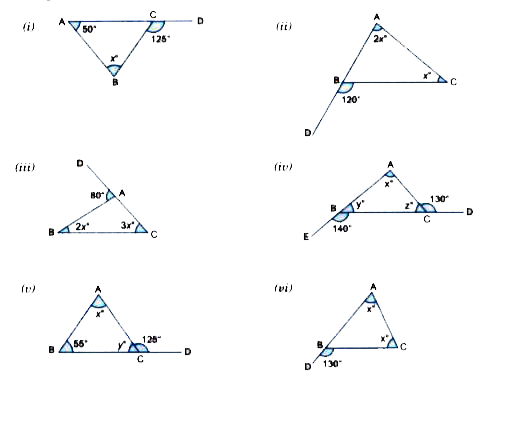
View SolutionIn each of the following figures, one side of a triangle has been produced. Find all the angles of the triangle in each case.
View SolutionCurrent the number of line segments drawn in each of the following figures and name them.

View Solution