In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle. The length of different line-segments are marked in each figure. Determine x, y, z in each case.
To solve the problem, we will use the properties of right-angled triangles and the relationships between the segments formed by the altitude drawn to the hypotenuse.
1. Identify the segments:
- Let AB=x
- Let BC=y
- Let AC=z
- The segments on the hypotenuse are AD=4 and DC=5. Therefore, AC=AD+DC=4+5=9.
2. Using the first formula:
- According to the property of right triangles, we have:
AB2=AD⋅AC
- Substituting the known values:
x2=4⋅9
- This simplifies to:
x2=36
- Taking the square root gives:
x=√36=6
3. Using the second formula:
- For segment BC:
BC2=DC⋅AC
- Substituting the known values:
y2=5⋅9
- This simplifies to:
y2=45
- Taking the square root gives:
y=√45=3√5
4. Using the third formula:
- For segment BD:
BD2=AD⋅DC
- Substituting the known values:
z2=4⋅5
- This simplifies to:
z2=20
- Taking the square root gives:
z=√20=2√5
Final Answers:
- x=6
- y=3√5
- z=2√5
- Let AB=x
- Let BC=y
- Let AC=z
- The segments on the hypotenuse are AD=4 and DC=5. Therefore, AC=AD+DC=4+5=9.
- According to the property of right triangles, we have:
AB2=AD⋅AC
- Substituting the known values:
x2=4⋅9
- This simplifies to:
x2=36
- Taking the square root gives:
x=√36=6
- For segment BC:
BC2=DC⋅AC
- Substituting the known values:
y2=5⋅9
- This simplifies to:
y2=45
- Taking the square root gives:
y=√45=3√5
- For segment BD:
BD2=AD⋅DC
- Substituting the known values:
z2=4⋅5
- This simplifies to:
z2=20
- Taking the square root gives:
z=√20=2√5
- x=6
- y=3√5
- z=2√5
Topper's Solved these Questions
Similar Questions
In each of the figures given below. Find x and y
View SolutionIn each of the figures given below, find whether AB∣∣CD

View SolutionIn each of the figures given below, find whether AB∣∣CD

View SolutionIn each of the figures [4.222 (i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segments are marked. Find the value of x in each of the following: (FIGURE)
View SolutionIn each of the following figures, find the values of x and y

View SolutionIn each of the figures given below, AB∣∣CD. Find the unknown angles, giving reasons
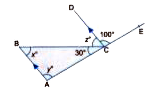
View SolutionIn each of the figures given below, AB∣∣CD. Find the unknown angles, giving reasons
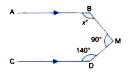
View SolutionIn each of the figures given below, AB∣∣CD. Find the unknown angles, giving reasons

View SolutionIn each of the figures given below, AB∣∣CD. Find the unknown angles, giving reasons

View SolutionIn each of the figures given below, AB∣∣CD. Find the unknown angles, giving reasons
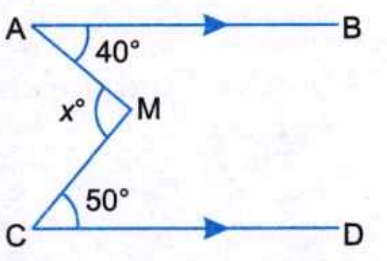
View Solution
