In the given figure, show that AB∣∣EF.
To prove that lines AB and EF are parallel, we will follow a step-by-step approach using the properties of angles formed by a transversal intersecting two lines.
1. Identify the Lines and Transversal:
- We have two lines AB and EF, and we will use line CD as a transversal that intersects both AB and EF.
2. Prove AB is Parallel to CD:
- Observe the angles formed by the transversal CD with line AB. Let’s denote the angle ∠ABC as 66° (given).
- Now, we also have another angle ∠BCD which is equal to 66° (since it is given that angle ABC = angle BCD).
- Since ∠ABC and ∠BCD are alternate interior angles and they are equal, we can conclude that:
AB∥CD(by the Alternate Interior Angles Theorem)
3. Prove EF is Parallel to CD:
- Now, we will consider line EF and the transversal CD. Let’s denote the angles formed as ∠CEF = 150° and ∠ECD = 30°.
- The sum of these angles is:
∠CEF+∠ECD=150°+30°=180°
- Since the interior angles on the same side of the transversal (∠CEF and ∠ECD) are supplementary, we can conclude that:
EF∥CD(by the Consecutive Interior Angles Theorem)
4. Conclude AB is Parallel to EF:
- Now that we have established that AB is parallel to CD and EF is also parallel to CD, we can use the transitive property of parallel lines:
AB∥EF(if two lines are both parallel to a third line, they are parallel to each other)
Final Conclusion:
Thus, we have shown that AB is parallel to EF.
---
- We have two lines AB and EF, and we will use line CD as a transversal that intersects both AB and EF.
- Observe the angles formed by the transversal CD with line AB. Let’s denote the angle ∠ABC as 66° (given).
- Now, we also have another angle ∠BCD which is equal to 66° (since it is given that angle ABC = angle BCD).
- Since ∠ABC and ∠BCD are alternate interior angles and they are equal, we can conclude that:
AB∥CD(by the Alternate Interior Angles Theorem)
- Now, we will consider line EF and the transversal CD. Let’s denote the angles formed as ∠CEF = 150° and ∠ECD = 30°.
- The sum of these angles is:
∠CEF+∠ECD=150°+30°=180°
- Since the interior angles on the same side of the transversal (∠CEF and ∠ECD) are supplementary, we can conclude that:
EF∥CD(by the Consecutive Interior Angles Theorem)
- Now that we have established that AB is parallel to CD and EF is also parallel to CD, we can use the transitive property of parallel lines:
AB∥EF(if two lines are both parallel to a third line, they are parallel to each other)
Thus, we have shown that AB is parallel to EF.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The given figure shows______
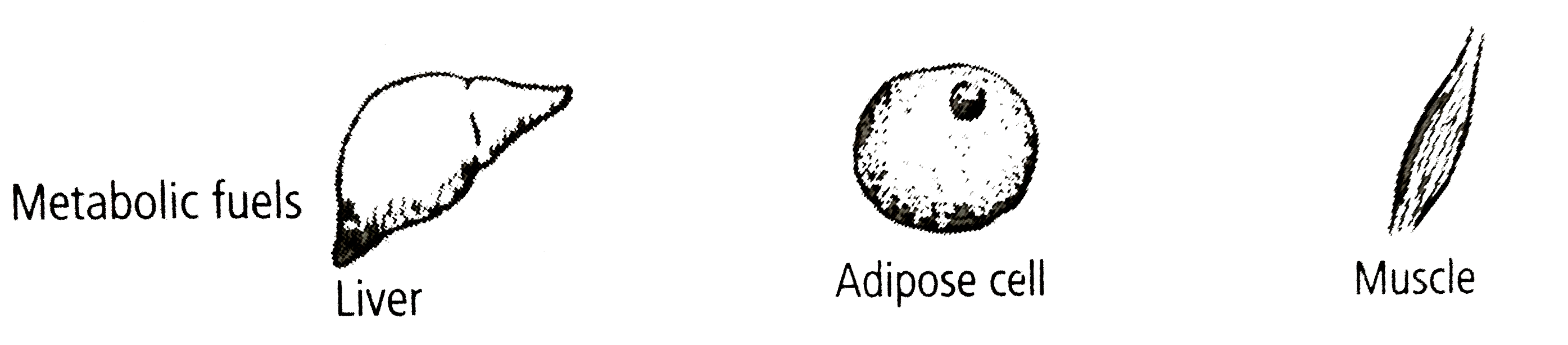 Athe major target sites and the metabolic actions of the anabolic homone secreted by the beta cells of heterocrine glandBthe major target sites and the metabolic action of the hormone secreted by alpha cells of pancreasCthe major target sites and the functions of the hormone secreted by the anterior pituitary gland.Dthe major target sites and the metabolic actions of the hormone secreted by the parafollicular C cells
Athe major target sites and the metabolic actions of the anabolic homone secreted by the beta cells of heterocrine glandBthe major target sites and the metabolic action of the hormone secreted by alpha cells of pancreasCthe major target sites and the functions of the hormone secreted by the anterior pituitary gland.Dthe major target sites and the metabolic actions of the hormone secreted by the parafollicular C cellsThe given figure shows an example of
 Ahomologous organsBconvergent evolutionCdivergent evolutionDboth a and c
Ahomologous organsBconvergent evolutionCdivergent evolutionDboth a and cThe given figure shows lateral view of the human brain.Identify the parts labelled as A to E and select the correct option.
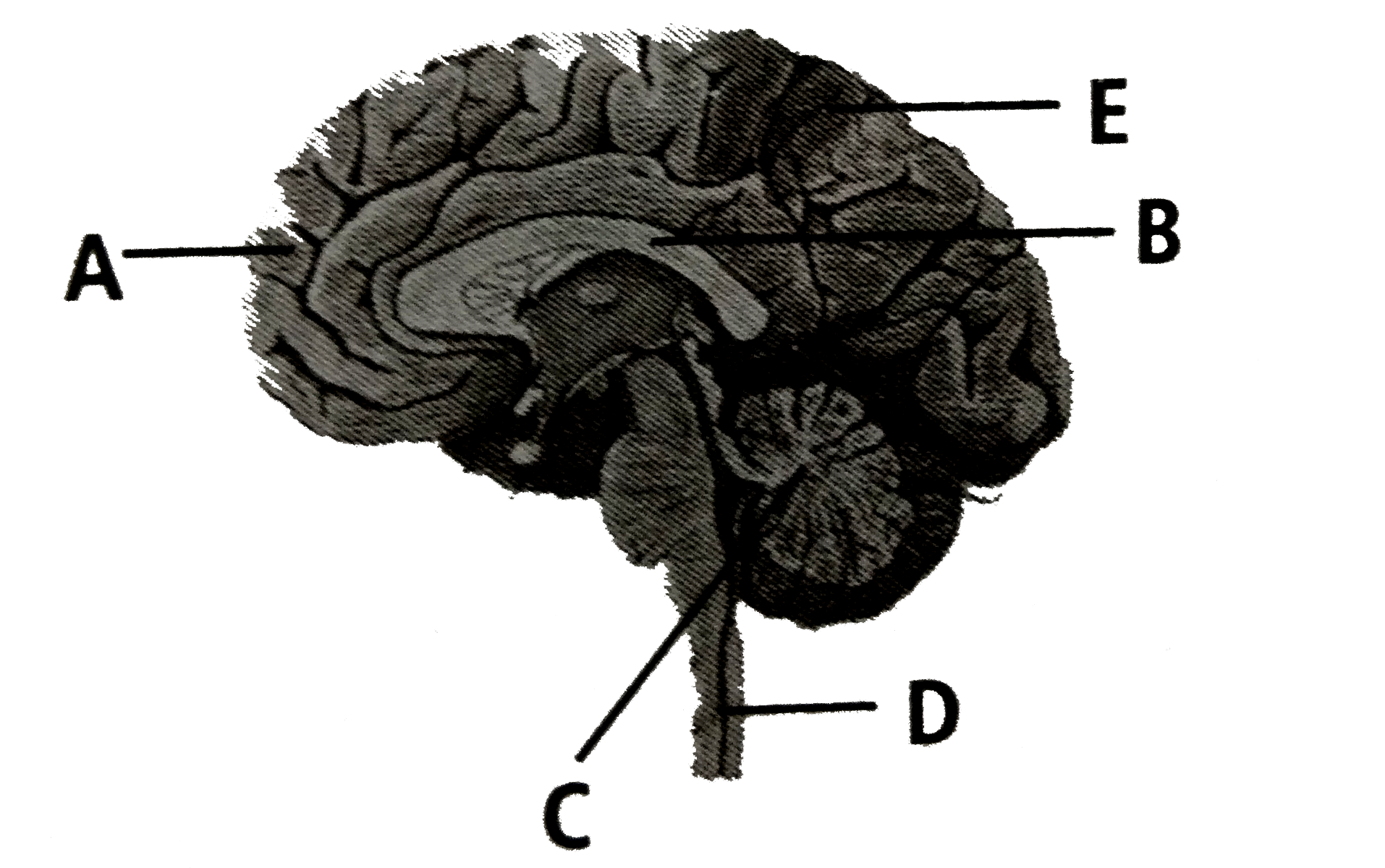 AABCDETemporal lobeCorpus callosumCerebrumMedulla oblongataFrontal lobeBABCDEFrontal lobeThalamusCerebrumMedulla oblongataOccipital lobeCABCDETemporal lobePonsCerebrumMedulla oblongataFrontal lobeDABCDEFrontal lobeCorpus callosumCerebellumMedulla oblongataParietal lobe
AABCDETemporal lobeCorpus callosumCerebrumMedulla oblongataFrontal lobeBABCDEFrontal lobeThalamusCerebrumMedulla oblongataOccipital lobeCABCDETemporal lobePonsCerebrumMedulla oblongataFrontal lobeDABCDEFrontal lobeCorpus callosumCerebellumMedulla oblongataParietal lobe
In Figure, Show that AB ∣∣ EF.
View Solution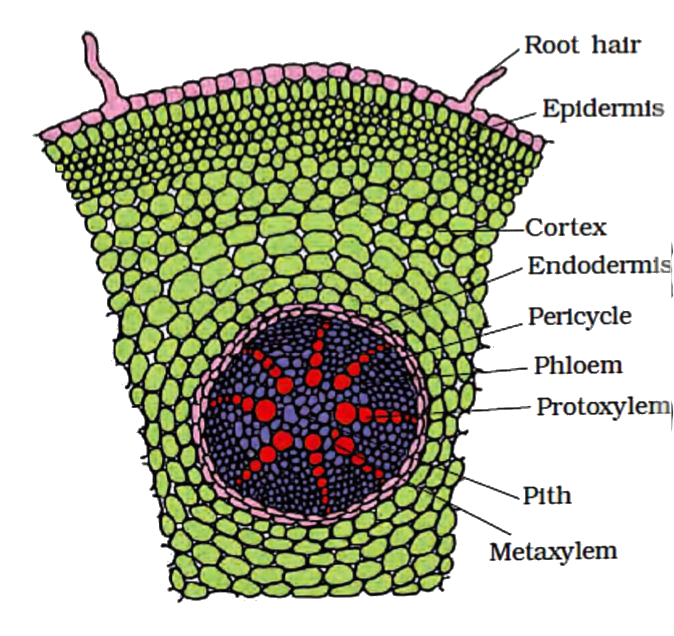
The given figure shows T.S of
View SolutionIn the given figure, if AB || CD and CD || EF, find ∠ACE.
View SolutionThe given figure shows that two parallel lines cut by the transversal AB. If ∠a:∠b=4:5, find the angles a,b,c,d,e and x.
View SolutionIn the given figure A, B and C are points on OP, OQ and OR respectively such that AB||PQ and BC||QR. Show that AC||PR.

View Solution

