In Fig. 15.35, AOBCA represents a quadrant of a circle of radius 3.5 cm with centre O . Calculate the area of the shaded portion (Take π=22/7) .
To solve the problem of calculating the area of the shaded portion in the quadrant of a circle with radius 3.5 cm, we can follow these steps:
Step 1: Calculate the area of the quadrant
The area of a quadrant of a circle can be calculated using the formula:
Area of Quadrant=14×πr2
where r is the radius of the circle.
Given that the radius r=3.5 cm, we can substitute this value into the formula.
Step 2: Substitute the values into the formula
Using π=227:
Area of Quadrant=14×227×(3.5)2
Step 3: Calculate (3.5)2
Calculating (3.5)2:
(3.5)2=12.25
Step 4: Substitute (3.5)2 back into the area formula
Now substituting back:
Area of Quadrant=14×227×12.25
Step 5: Calculate the area
Calculating the area:
Area of Quadrant=22×12.254×7
Calculating 22×12.25:
22×12.25=270.5
Now substituting this value:
Area of Quadrant=270.528
Step 6: Final calculation
Now divide 270.5 by 28:
Area of Quadrant≈9.6464 cm2
Step 7: Conclusion
Thus, the area of the quadrant is approximately 9.6464 cm2.
The area of a quadrant of a circle can be calculated using the formula:
Area of Quadrant=14×πr2
where r is the radius of the circle.
Using π=227:
Area of Quadrant=14×227×(3.5)2
Calculating (3.5)2:
(3.5)2=12.25
Now substituting back:
Area of Quadrant=14×227×12.25
Calculating the area:
Area of Quadrant=22×12.254×7
Calculating 22×12.25:
22×12.25=270.5
Now substituting this value:
Area of Quadrant=270.528
Now divide 270.5 by 28:
Area of Quadrant≈9.6464 cm2
Thus, the area of the quadrant is approximately 9.6464 cm2.
Topper's Solved these Questions
Similar Questions
AOBC is a quadrant of a circle of radius 10 cm. Calculate the area of the shaded portion. (Use π=3.14)
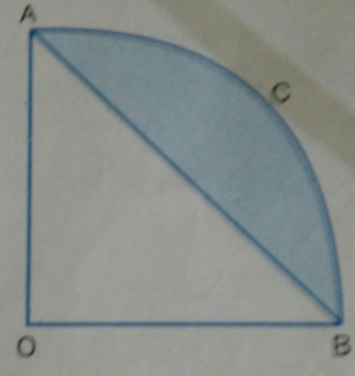
View SolutionFind the area of a circle with radius 3.5cm.
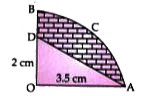
View SolutionIn the figure alongside, OAB is a quadrant of a circle. The radius OA = 3.5 cm and OD = 2 cm. Calculate the area of ther shaded portion.
(Take π=227)
View SolutionABCP is a quadrant of a circle of radius 14 cm. with AC as diameter, a semicircle is drawn. Find the area of the shaded portion
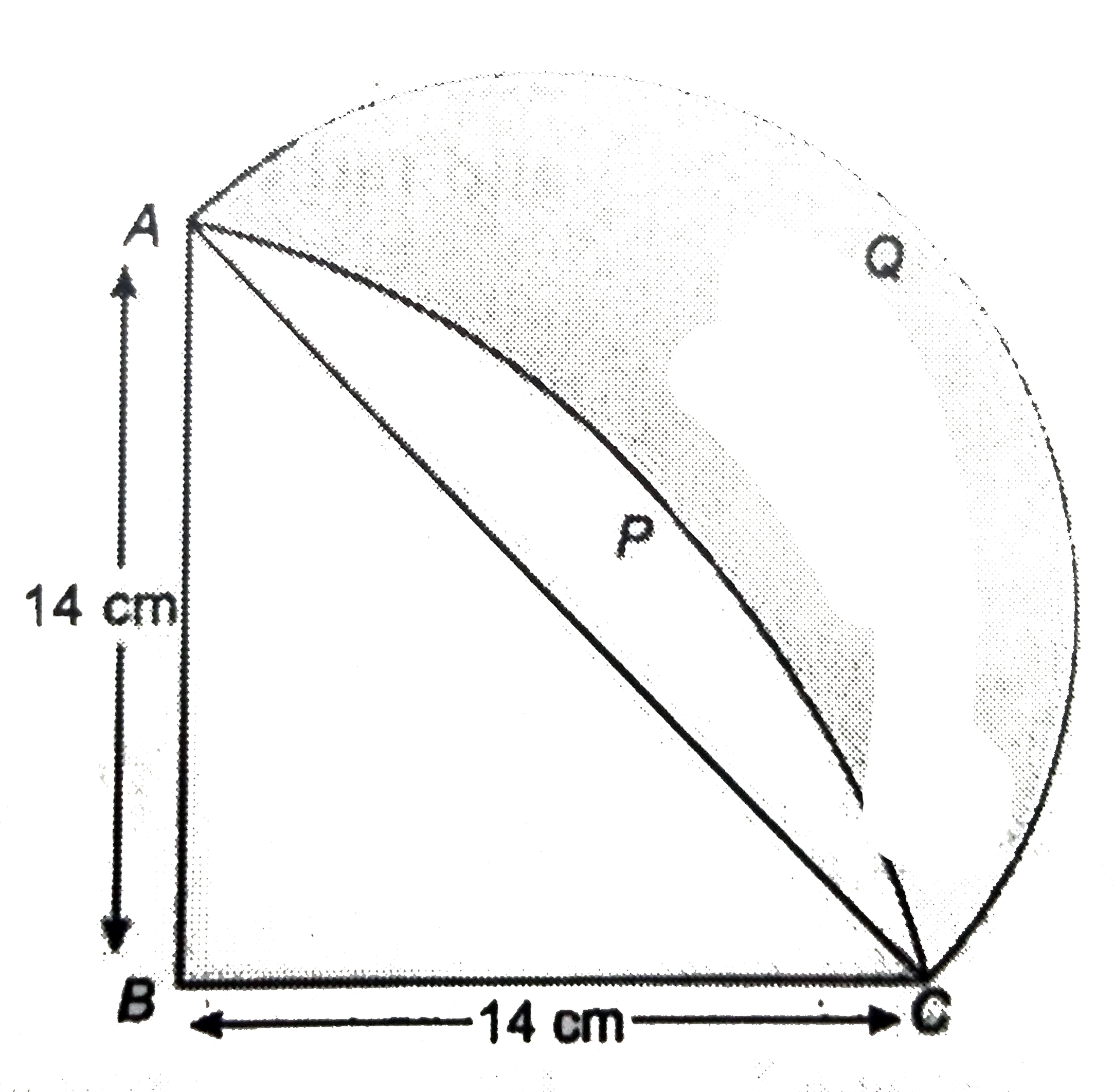
View SolutionABCP is a quadrant of a circle of radius 14 cm. With AC as diameter, a semi-circle is drawn. Find the area of the shaded portion.
View SolutionIn Figure, ABC is an equilateral triangle inscribed in a circle of radius 4 cm with centre O . Find the area of the shaded region.
View SolutionIn Fig. 12.33, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
View SolutionIn Fig. 12.33, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
View SolutionIn Figure, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O , then find the area of the shaded region. (Use π=22/7)
View SolutionIn Fig. 15.99, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA=21 cm , find the area of the shaded region. (FIGURE)
View Solution
