In Figure, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O , then find the area of the shaded region. (Use π=22/7)
To find the area of the shaded region in the given figure, we will follow these steps:
Step 1: Calculate the area of the square OABC.
The side of the square is given as 7 cm. The area of a square is calculated using the formula:
Area of square=side2
Substituting the value:
Area of square=72=49cm2
Step 2: Determine the radius of the quadrant.
Since OABC is a quadrant of a circle and the center is at O, the radius of the circle is equal to the side of the square. Thus,
Radius(R)=7cm
Step 3: Calculate the area of the sector OAPC.
The angle of the sector for a quadrant is 90 degrees. The area of a sector is given by the formula:
Area of sector=θ360∘×πR2
Substituting the values:
Area of sector=90360×227×(7)2
Calculating this step by step:
1. Calculate 90360=14.
2. Calculate R2=72=49.
3. Substitute into the formula:
Area of sector=14×227×49
4. Simplify:
Area of sector=22×494×7=22×74=1544=38.5cm2
Step 4: Calculate the area of the shaded region.
The area of the shaded region can be found by subtracting the area of the sector from the area of the square:
Area of shaded region=Area of square−Area of sector
Substituting the values:
Area of shaded region=49−38.5=10.5cm2
Final Answer:
The area of the shaded region is 10.5cm2.
---
The side of the square is given as 7 cm. The area of a square is calculated using the formula:
Since OABC is a quadrant of a circle and the center is at O, the radius of the circle is equal to the side of the square. Thus,
The angle of the sector for a quadrant is 90 degrees. The area of a sector is given by the formula:
2. Calculate R2=72=49.
3. Substitute into the formula:
The area of the shaded region can be found by subtracting the area of the sector from the area of the square:
The area of the shaded region is 10.5cm2.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the figure above, OABC is a square and B is a points on the circle with center O. If AB=6, what is the area of the shaded region?A9(π−2)B9(π−1)C12(π−2)D18(π−2)
In Figure, ABCD is a trapezium of area 24.5 cm2 . In it, AD∣∣BC , ∠DAB=90∘ , AD=10 cm and BC=4 cm . If ABE is a quadrant of a circle, find the area of the shaded region. (Take π=22/7) .
View SolutionIn Figure, ABCD is a trapezium with AB∣∣DC and ∠BCD=60∘ . If BFEC is a sector of a circle with centre C and AB=BC=7 cm and DE=4 cm , then find the area of the shaded region (Use π=227 and √3=1.732) .
View SolutionIn Fig. 15.35, AOBCA represents a quadrant of a circle of radius 3.5 cm with centre O . Calculate the area of the shaded portion (Take π=22/7) .
View SolutionIn Fig. 15.99, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA=21 cm , find the area of the shaded region. (FIGURE)
View SolutionIn Figure ABCD is a square with side 7 cm. A circle is drawn circumscribing the square . Find the area of the shaded region .

View SolutionIn Figure , a square OPQR is inscribed in a quadrant OAQB of a circle. If the radius of circle is 6√2 cm, find the area of the shaded region
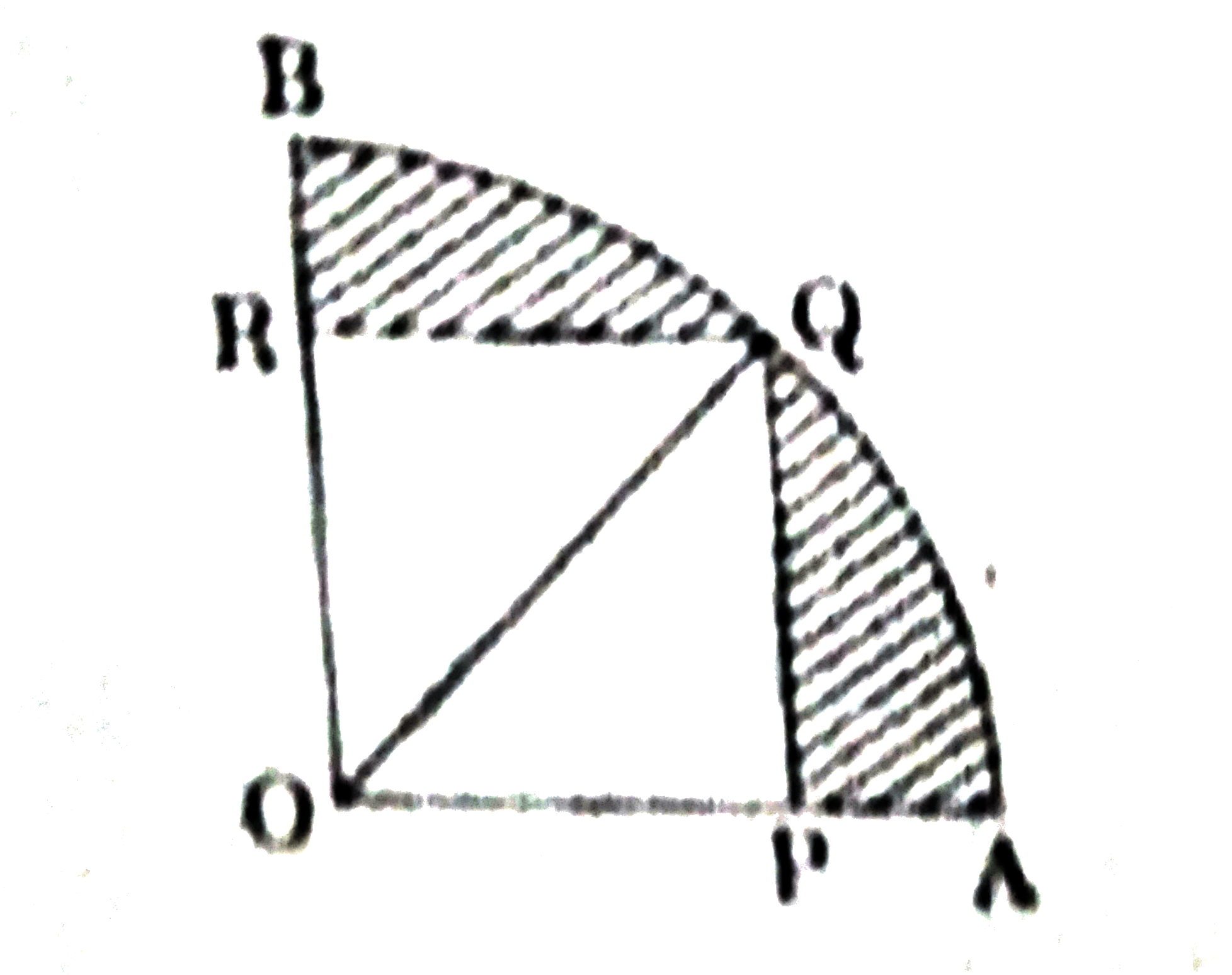
View SolutionIn Figure-9, a square OPQR is inscribed in a quadrant OAQB of a circle. If the radius of circle is 6√2 cm, Find the area of the shaded region.
View Solution
