An object is placed far away from all theobjects that can exert force on it. A frame of reference is constructed by taking the origin and axes fixed in this object. Will the fraame be necessarily inertial?
To determine whether the frame of reference constructed by taking the origin and axes fixed in an object placed far away from all other objects that can exert force on it is necessarily inertial, we can follow these steps:
1. Understanding Frame of Reference:
A frame of reference is a coordinate system used to measure the position and motion of objects. It includes both spatial coordinates and a time frame.
2. Identifying the Object's Condition:
The object in question is placed far away from all other objects that can exert forces on it. This implies that it is isolated and not influenced by external forces.
3. Applying Newton's First Law:
According to Newton's First Law of Motion, an object at rest remains at rest, and an object in motion continues in motion with a constant velocity unless acted upon by a net external force. Since the object is far from other forces, we can assume that it experiences no net external force.
4. Determining Acceleration:
Since the object is free from external forces, its acceleration must be zero (a = 0). This means that it will either remain at rest or move with a constant velocity.
5. Frame of Reference Fixed in the Object:
The frame of reference is fixed in the object itself. If the object is not accelerating (a = 0), then the laws of motion (Newton's laws) apply in this frame.
6. Conclusion:
Since the object is not accelerating and the frame of reference is fixed in it, this frame of reference must be an inertial frame. Therefore, the frame of reference constructed in this situation is necessarily inertial.
Final Answer:
Yes, the frame of reference will be necessarily inertial.
---
A frame of reference is a coordinate system used to measure the position and motion of objects. It includes both spatial coordinates and a time frame.
The object in question is placed far away from all other objects that can exert forces on it. This implies that it is isolated and not influenced by external forces.
According to Newton's First Law of Motion, an object at rest remains at rest, and an object in motion continues in motion with a constant velocity unless acted upon by a net external force. Since the object is far from other forces, we can assume that it experiences no net external force.
Since the object is free from external forces, its acceleration must be zero (a = 0). This means that it will either remain at rest or move with a constant velocity.
The frame of reference is fixed in the object itself. If the object is not accelerating (a = 0), then the laws of motion (Newton's laws) apply in this frame.
Since the object is not accelerating and the frame of reference is fixed in it, this frame of reference must be an inertial frame. Therefore, the frame of reference constructed in this situation is necessarily inertial.
Yes, the frame of reference will be necessarily inertial.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Exercises
42 Videos
- LAWS OF THERMODYNAMICSBOOK - HC VERMA ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - All Questions
64 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Question for short Answer
14 Videos
Similar Questions
A body is uniformly rotating bout an axis fixed in an inertial frame of reference. Let →A be a unit vector along the axis of rotation and →B be the unit vector along the resultant force on a particle P of the body away from the axis. The value of →A.→B is
View SolutionThe acceleration of a particle is zero as measured from an inertial frame of reference. Can we conclude that no force acts on the particle?
View SolutionEinstein in 1905 proppunded the special theory of relativity and in 1915 proposed the general theory of relativity. The special theory deals with inertial frames of reference. The general theory of relativity deals with problems in which one frame of reference. He assumed that fixed frame is accelerated w.r.t. another frame of reference of reference cannot be located. Postulated of special theory of realtivity
● The laws of physics have the same form in all inertial systems.
● The velocity light in empty space is a unicersal constant the same for all observers.
● Einstein proved the following facts based on his theory of special relativity. Let v be the velocity of the speceship w.r.t a given frame of reference. The obserations are made by an observer in that reference frame.
● All clocks on the spaceship wil go slow by a factor √1−v2/c2
● All objects on the spaceship will have contracted in length by a factor √1−v2/c2
● The mass of the spaceship increases by a factor √1−v2/c2
● Mass and energy are interconvertable E=mc2
The speed of a meterial object can never exceed the velocity of light.
● If two objects A and B are moving with velocity u and v w.r.t each other along the x-axis, the relative velocity of A w.r.t. B=u−v1−uv/v2
A stationary body explodes into two fragments each of rest mass 1kg that move apart at speed of 0.6c relative to the original body. The rest mass of the original body is -
View SolutionEinstein in 1905 proppunded the special theory of relativity and in 1915 proposed the general theory of relativity. The special theory deals with inertial frames of reference. The general theory of relativity deals with problems in which one frame of reference. He assumed that fixed frame is accelerated w.r.t. another frame of reference of reference cannot be located. Postulated of special theory of realtivity
● The laws of physics have the same form in all inertial systems.
● The velocity light in empty space is a unicersal constant the same for all observers.
● Einstein proved the following facts based on his theory of special relativity. Let v be the velocity of the speceship w.r.t a given frame of reference. The obserations are made by an observer in that reference frame.
● All clocks on the spaceship wil go slow by a factor √1−v2/c2
● All objects on the spaceship will have contracted in length by a factor √1−v2/c2
● The mass of the spaceship increases by a factor √1−v2/c2
● Mass and energy are interconvertable E=mc2
The speed of a meterial object can never exceed the velocity of light.
● If two objects A and B are moving with velocity u and v w.r.t each other along the x-axis, the relative velocity of A w.r.t. B=u−v1−uv/v2
The momentum of an electron moving with a speed 0.6c (Rest mass of electron is 9.1×10−31kg)
View SolutionEinstein in 1905 proppunded the special theory of relativity and in 1915 proposed the general theory of relativity. The special theory deals with inertial frames of reference. The general theory of relativity deals with problems in which one frame of reference. He assumed that fixed frame is accelerated w.r.t. another frame of reference of reference cannot be located. Postulated of special theory of realtivity
● The laws of physics have the same form in all inertial systems.
● The velocity light in empty space is a unicersal constant the same for all observers.
● Einstein proved the following facts based on his theory of special relativity. Let v be the velocity of the speceship w.r.t a given frame of reference. The obserations are made by an observer in that reference frame.
● All clocks on the spaceship wil go slow by a factor √1−v2/c2
● All objects on the spaceship will have contracted in length by a factor √1−v2/c2
● The mass of the spaceship increases by a factor √1−v2/c2
● Mass and energy are interconvertable E=mc2
The speed of a meterial object can never exceed the velocity of light.
● If two objects A and B are moving with velocity u and v w.r.t each other along the x-axis, the relative velocity of A w.r.t. B=u−v1−uv/v2
One cosmic ray particle appraches the earth along its axis with a velocity of 0.9c towards the north the and another one with a velocity of 0.5c towards the south pole. The relative speed of approcach of one particle w.r.t. another is-
View SolutionA frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity ω is an example of non=inertial frame of reference. The relationship between the force →Frot experienced by a particle of mass m moving on the rotating disc and the force →F∈ experienced by the particle in an inertial frame of reference is
→Frot=→Fin+2m(→vrot×→ω)+m(→ω×→r)×→ω.
where →vrot is the velocity of the particle in the rotating frame of reference and →r is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed ω about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (→ω=ωˆk). A small block of mass m is gently placed in the slot at →r(R/2)ˆi at t=0 and is constrained to move only along the slot.
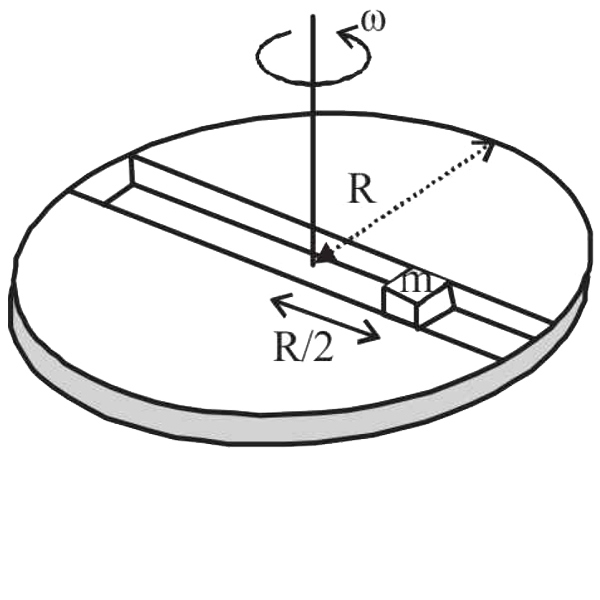
The distance r of the block at time is
View SolutionA frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity ω is an example of non=inertial frame of reference. The relationship between the force →Frot experienced by a particle of mass m moving on the rotating disc and the force →F∈ experienced by the particle in an inertial frame of reference is
→Frot=→Fin+2m(→vrot×→ω)+m(→ω×→r)×→ω.
where →vrot is the velocity of the particle in the rotating frame of reference and →r is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed ω about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (→ω=ωˆk). A small block of mass m is gently placed in the slot at →r(R/2)ˆi at t=0 and is constrained to move only along the slot.
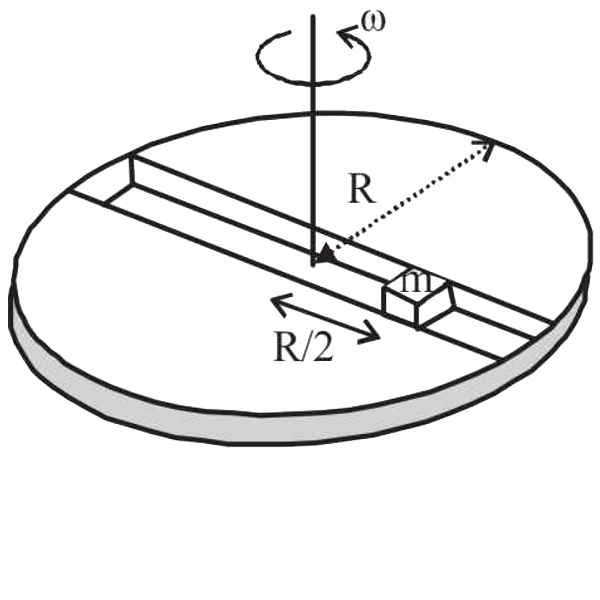
The net reaction of the disc on the block is
View SolutionAn object is placed at a distance of 30 cm from a converging lens of focal length 15 cm. A normal eye (near point 25 cm, far point infinity) is placed close to the lens on the other side. (a) Can the eye see the object clearly? (b) What should be the minimum separation between the lens and the eye so that the eye can clearly see the object? c. Can a diverging lens, placed in contact with the converging lens, help in seeing the object clearly when the eye is close to the lens?
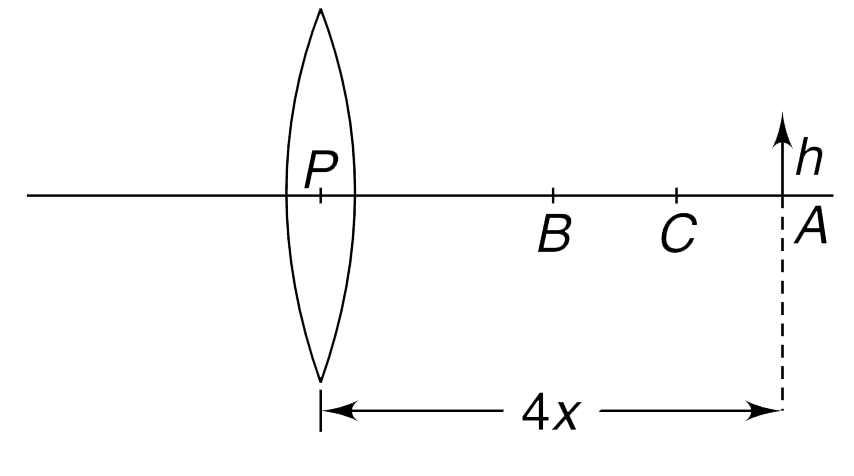
View SolutionA thin converging lens forms a real image of an object located far away from the lens. The image is formed at A at a distance 4x from the lens and height of the image is h. A thin diverging lens of focal length x is placed at B[PB=2x] and a converging lens of focal length 2x is placed at C[PC=3x]. The principal axes of all lenses coincide. Find the height of the final image formed.
View Solution(A) : An object placed on the rotating hori- zontal table may fly off at lower angular velocity when placed far away from the axis.
(R ) : An object placed at the edge of the rotating table experiences more centrifugal force than at nearer position relative to the table
View Solution
