Question

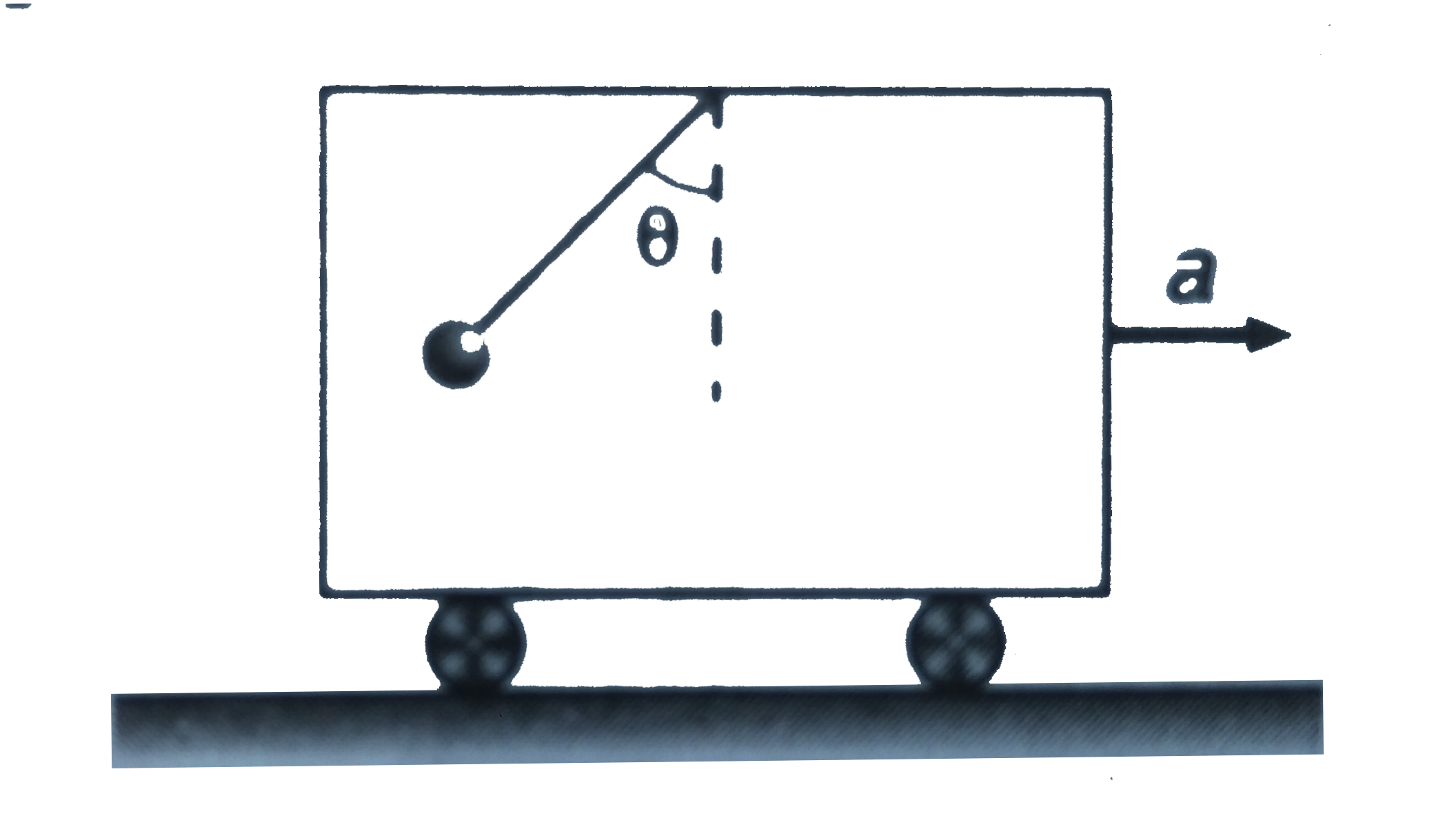
A plumb bob is hung from the ceiling of a train compartment. If the train moves with an acceleration a along a straight horizontal track, the string supporting the bob makes an angle ${\tan }^1\left(\frac{a}{g}\right)$ with the normal to the ceiling. Suppose the train moves on an inclined straight track with uniform velocity, if the angle of incline is ${\tan }^{-1}\left(\frac{a}{g}\right)$, the string again makes the same angle with the normal to the ceiling. Can a person sitting inside the compartment tell by looking at the plumb line whether the train is accelerated on a horizontal straight track or it is going on an incline? If yes, how? If no, suggest a method to do so.

Explanation

To determine whether a person sitting inside a train compartment can tell if the train is accelerating on a horizontal track or moving on an incline with uniform velocity, we can analyze the forces acting on a plumb bob hung from the ceiling of the compartment in both scenarios.

1. Understanding the Setup:
- A plumb bob is suspended from the ceiling of a train compartment.
- In the first case, the train is accelerating horizontally with acceleration \( a \).
- In the second case, the train is moving on an incline with an angle of incline \( \theta = \tan^{-1}(a/g) \).

2. Analyzing Forces in the Horizontal Acceleration Case:
- When the train accelerates horizontally, the plumb bob will not hang vertically. Instead, it will make an angle \( \theta \) with the vertical.
- The angle \( \theta \) can be expressed as:
\( \theta = \tan^{-1}\left(\frac{a}{g}\right) \)
- The forces acting on the bob are:
- Weight \( W = mg \) acting downward.
- Tension \( T \) in the string acting along the string, making an angle \( \theta \) with the vertical.
- The vertical component of tension balances the weight:
\( T \cos \theta = mg \)
- The horizontal component of tension provides the necessary force for the bob to accelerate with the train:
\( T \sin \theta = ma \)

3. Analyzing Forces in the Inclined Motion Case:
- In the second case, where the train is moving on an incline, the bob will also make the same angle \( \theta \) with the vertical.
- The forces acting on the bob are similar:
- Weight \( W = mg \) acting downward.
- Tension \( T \) acting along the string.
- The vertical component of tension still balances the weight:
\( T \cos \theta = mg \)
- However, since the train is moving at a constant velocity on an incline, there is no horizontal acceleration, and thus:
\( T \sin \theta = 0 \)

4. Comparing Tension in Both Cases:
- From the equations derived:
- In the accelerating case:
\( T = \frac{mg}{\cos \theta} \)
- In the inclined case:
\( T = mg \)
- The tension in the string is greater when the train is accelerating horizontally than when it is moving on an incline.

5. Conclusion:
- A person sitting inside the compartment cannot tell if the train is accelerating or moving on an incline just by observing the angle of the plumb bob, as it appears the same in both cases.
- However, they can distinguish between the two scenarios by using a spring balance to measure the tension in the string. If the tension is greater than \( mg \), the train is accelerating; if it is equal to \( mg \), the train is on an incline moving at a constant velocity.